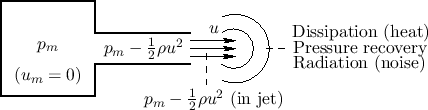Properties of Gases
Particle Velocity of a Gas
The particle velocity of a gas flow at any point can be defined as the average velocity (in meters per second, m/s) of the air molecules passing through a plane cutting orthogonal to the flow. The term ``velocity'' in this book, when referring to air, means ``particle velocity.''
It is common in acoustics to denote particle velocity by lower-case
![]() .
.
Volume Velocity of a Gas
The volume velocity ![]() of a gas flow is defined as particle
velocity
of a gas flow is defined as particle
velocity ![]() times the cross-sectional area
times the cross-sectional area ![]() of the flow, or
of the flow, or
When a flow is confined within an enclosed channel, as it is in an
acoustic tube, volume velocity is conserved when the tube
changes cross-sectional area, assuming the density ![]() remains
constant. This follows directly from conservation of mass in a flow:
The total mass passing a given point
remains
constant. This follows directly from conservation of mass in a flow:
The total mass passing a given point ![]() along the flow is given by
the mass density
along the flow is given by
the mass density ![]() times the integral of the volume volume
velocity at that point, or
times the integral of the volume volume
velocity at that point, or
As a simple example, consider a constant flow through two cylindrical
acoustic tube sections having cross-sectional areas ![]() and
and ![]() ,
respectively. If the particle velocity in cylinder 1 is
,
respectively. If the particle velocity in cylinder 1 is ![]() , then
the particle velocity in cylinder 2 may be found by solving
, then
the particle velocity in cylinder 2 may be found by solving
It is common in the field of acoustics to denote volume velocity by an
upper-case ![]() . Thus, for the two-cylinder acoustic tube example above,
we would define
. Thus, for the two-cylinder acoustic tube example above,
we would define
![]() and
and
![]() , so that
, so that
Pressure is Confined Kinetic Energy
According the kinetic theory of ideal gases [180], air pressure can be defined as the average momentum transfer per unit area per unit time due to molecular collisions between a confined gas and its boundary. Using Newton's second law, this pressure can be shown to be given by one third of the average kinetic energy of molecules in the gas.
Proof: This is a classical result from the kinetic theory of gases
[180]. Let ![]() be the total mass of a gas
confined to a rectangular volume
be the total mass of a gas
confined to a rectangular volume ![]() , where
, where ![]() is the area of
one side and
is the area of
one side and ![]() the distance to the opposite side. Let
the distance to the opposite side. Let
![]() denote the average molecule velocity in the
denote the average molecule velocity in the ![]() direction. Then the
total net molecular momentum in the
direction. Then the
total net molecular momentum in the ![]() direction is given by
direction is given by
![]() . Suppose the momentum
. Suppose the momentum
![]() is directed
against a face of area
is directed
against a face of area ![]() . A rigid-wall elastic collision by a mass
. A rigid-wall elastic collision by a mass
![]() traveling into the wall at velocity
traveling into the wall at velocity
![]() imparts a momentum of
magnitude
imparts a momentum of
magnitude
![]() to the wall (because the momentum of the mass is
changed from
to the wall (because the momentum of the mass is
changed from
![]() to
to
![]() , and momentum is conserved).
The average momentum-transfer per unit area is therefore
, and momentum is conserved).
The average momentum-transfer per unit area is therefore
![]() at any instant in time. To obtain the definition of pressure, we need
only multiply by the average collision rate, which is given by
at any instant in time. To obtain the definition of pressure, we need
only multiply by the average collision rate, which is given by
![]() . That is, the average
. That is, the average ![]() -velocity divided by the
round-trip distance along the
-velocity divided by the
round-trip distance along the ![]() dimension gives the collision rate
at either wall bounding the
dimension gives the collision rate
at either wall bounding the ![]() dimension. Thus, we obtain
dimension. Thus, we obtain
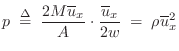
Bernoulli Equation
In an ideal inviscid, incompressible flow, we have, by conservation of energy,

This basic energy conservation law was published in 1738 by Daniel Bernoulli in his classic work Hydrodynamica.
From §B.7.3, we have that the pressure of a gas is
proportional to the average kinetic energy of the molecules making up
the gas. Therefore, when a gas flows at a constant height ![]() , some
of its ``pressure kinetic energy'' must be given to the kinetic energy
of the flow as a whole. If the mean height of the flow changes, then
kinetic energy trades with potential energy as well.
, some
of its ``pressure kinetic energy'' must be given to the kinetic energy
of the flow as a whole. If the mean height of the flow changes, then
kinetic energy trades with potential energy as well.
Bernoulli Effect
The Bernoulli effect provides that, when a gas such as air flows, its pressure drops. This is the basis for how aircraft wings work: The cross-sectional shape of the wing, called an aerofoil (or airfoil), forces air to follow a longer path over the top of the wing, thereby speeding it up and creating a net upward force called lift.
Figure B.8 illustrates the Bernoulli effect for the case
of a reservoir at constant pressure ![]() (``mouth pressure'') driving
an acoustic tube. Any flow inside the ``mouth'' is neglected. Within the
acoustic channel, there is a flow with constant particle velocity
(``mouth pressure'') driving
an acoustic tube. Any flow inside the ``mouth'' is neglected. Within the
acoustic channel, there is a flow with constant particle velocity ![]() .
To conserve energy, the pressure within the acoustic channel must drop
down to
.
To conserve energy, the pressure within the acoustic channel must drop
down to
![]() . That is, the flow kinetic energy subtracts
from the pressure kinetic energy within the channel.
. That is, the flow kinetic energy subtracts
from the pressure kinetic energy within the channel.
For a more detailed derivation of the Bernoulli effect, see, e.g., [179]. Further discussion of its relevance in musical acoustics is given in [144,197].
Air Jets
Referring again to Fig.B.8, the gas flow exiting the acoustic tube is shown as forming a jet. The jet ``carries its own pressure'' until it dissipates in some form, such as any combination of the following:
- heat (now allowing for ``friction'' in the flow),
- vortices (angular momentum),
- radiation (sound waves), or
- pressure recovery.
For a summary of more advanced aeroacoustics, including consideration of vortices, see [196]. In addition, basic textbooks on fluid mechanics are relevant [171].
Acoustic Intensity
Acoustic intensity may be defined by
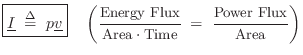
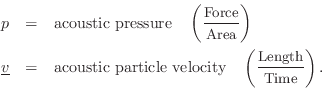
For a plane traveling wave, we have
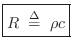
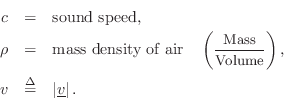
Therefore, in a plane wave,
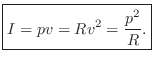
Acoustic Energy Density
The two forms of energy in a wave are kinetic and
potential. Denoting them at a particular time ![]() and position
and position
![]() by
by
![]() and
and
![]() , respectively, we can write them in
terms of velocity
, respectively, we can write them in
terms of velocity ![]() and wave impedance
and wave impedance ![]() as follows:
as follows:
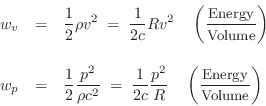
More specifically, ![]() and
and ![]() may be called the acoustic kinetic
energy density and the acoustic potential energy density, respectively.
may be called the acoustic kinetic
energy density and the acoustic potential energy density, respectively.
At each point in a plane wave, we have
![]() (pressure equals wave-impedance times velocity), and so
(pressure equals wave-impedance times velocity), and so
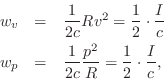
where
![]() denotes the acoustic
intensity (pressure times velocity) at time
denotes the acoustic
intensity (pressure times velocity) at time ![]() and position
and position
![]() .
Thus, half of the acoustic intensity
.
Thus, half of the acoustic intensity ![]() in a plane wave is kinetic,
and the other half is potential:B.30
in a plane wave is kinetic,
and the other half is potential:B.30
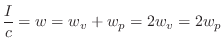
Energy Decay through Lossy Boundaries
Since the acoustic energy density ![]() is the energy per unit
volume in a 3D sound field, it follows that the total energy of the
field is given by integrating over the volume:
is the energy per unit
volume in a 3D sound field, it follows that the total energy of the
field is given by integrating over the volume:
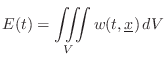
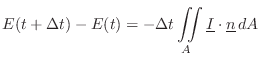
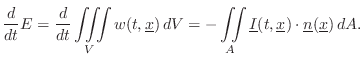
Sabine's theory of acoustic energy decay in reverberant room impulse responses can be derived using this conservation relation as a starting point.
Ideal Gas Law
The ideal gas law can be written as
where

The alternate form ![]() comes from the statistical
mechanics derivation in which
comes from the statistical
mechanics derivation in which ![]() is the number of gas molecules in
the volume, and
is the number of gas molecules in
the volume, and ![]() is Boltzmann's constant. In this
formulation (the kinetic theory of ideal gases), the
average kinetic
energy of the gas molecules is given by
is Boltzmann's constant. In this
formulation (the kinetic theory of ideal gases), the
average kinetic
energy of the gas molecules is given by ![]() . Thus,
temperature is proportional to average kinetic energy of the
gas molecules, where the kinetic energy of a molecule
. Thus,
temperature is proportional to average kinetic energy of the
gas molecules, where the kinetic energy of a molecule ![]() with
translational speed
with
translational speed ![]() is given by
is given by ![]() .
.
In an ideal gas, the molecules are like little rubber balls (or rubbery assemblies of rubber balls) in a weightless vacuum, colliding with each other and the walls elastically and losslessly (an ``ideal rubber''). Electromagnetic forces among the molecules are neglected, other than the electron-orbital repulsion producing the elastic collisions; in other words, the molecules are treated as electrically neutral far away. (Gases of ionized molecules are called plasmas.)
The mass ![]() of the gas in volume
of the gas in volume ![]() is given by
is given by ![]() , where
, where ![]() is
the molar mass of the gass (about 29 g per mole for air). The
air density is thus
is
the molar mass of the gass (about 29 g per mole for air). The
air density is thus ![]() so that we can write
so that we can write
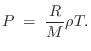
We normally do not need to consider the (nonlinear) ideal gas law in
audio acoustics because it is usually linearized about some
ambient pressure ![]() . The physical pressure is then
. The physical pressure is then ![]() , where
, where
![]() is the usual acoustic pressure-wave variable. That is, we are
only concerned with small pressure perturbations
is the usual acoustic pressure-wave variable. That is, we are
only concerned with small pressure perturbations ![]() in typical
audio acoustics situations, so that, for example, variations in volume
in typical
audio acoustics situations, so that, for example, variations in volume
![]() and density
and density ![]() can be neglected. Notable exceptions include
brass instruments which can achieve nonlinear sound-pressure regions,
especially near the mouthpiece [198,52].
Additionally, the aeroacoustics of air jets is nonlinear
[196,530,531,532,102,101].
can be neglected. Notable exceptions include
brass instruments which can achieve nonlinear sound-pressure regions,
especially near the mouthpiece [198,52].
Additionally, the aeroacoustics of air jets is nonlinear
[196,530,531,532,102,101].
Isothermal versus Isentropic
If air compression/expansion were isothermal (constant
temperature ![]() ), then, according to the ideal gas law
), then, according to the ideal gas law ![]() , the
pressure
, the
pressure ![]() would simply be proportional to density
would simply be proportional to density ![]() . It turns
out, however, that heat diffusion is much slower than audio acoustic
vibrations. As a result, air compression/expansion is much closer to
isentropic (constant entropy
. It turns
out, however, that heat diffusion is much slower than audio acoustic
vibrations. As a result, air compression/expansion is much closer to
isentropic (constant entropy ![]() ) in normal acoustic
situations. (An isentropic process is also called a reversible
adiabatic process.) This means that when air is compressed by
shrinking its volume
) in normal acoustic
situations. (An isentropic process is also called a reversible
adiabatic process.) This means that when air is compressed by
shrinking its volume ![]() , for example, not only does the pressure
, for example, not only does the pressure ![]() increase (§B.7.3), but the temperature
increase (§B.7.3), but the temperature ![]() increases as
well (as quantified in the next section). In a constant-entropy
compression/expansion, temperature changes are not given time to
diffuse away to thermal equilibrium. Instead, they remain largely
frozen in place. Compressing air heats it up, and relaxing the
compression cools it back down.
increases as
well (as quantified in the next section). In a constant-entropy
compression/expansion, temperature changes are not given time to
diffuse away to thermal equilibrium. Instead, they remain largely
frozen in place. Compressing air heats it up, and relaxing the
compression cools it back down.
Adiabatic Gas Constant
The relative amount of compression/expansion energy that goes into
temperature ![]() versus pressure
versus pressure ![]() can be characterized by the heat capacity ratio
can be characterized by the heat capacity ratio
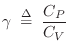
In terms of ![]() , we have
, we have
where
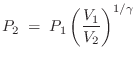
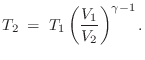
The value
![]() is typical for any diatomic
gas.B.31 Monatomic inert gases, on the other hand,
such as Helium, Neon, and Argon, have
is typical for any diatomic
gas.B.31 Monatomic inert gases, on the other hand,
such as Helium, Neon, and Argon, have
![]() . Carbon
dioxide, which is triatomic, has a heat capacity ratio
. Carbon
dioxide, which is triatomic, has a heat capacity ratio
![]() . We see that more complex molecules have lower
. We see that more complex molecules have lower ![]() values because they can store heat in more degrees of freedom.
values because they can store heat in more degrees of freedom.
Heat Capacity of Ideal Gases
In statistical thermodynamics [175,138],
it is derived that each molecular degree of freedom contributes ![]() to the molar heat capacity of an ideal gas, where again
to the molar heat capacity of an ideal gas, where again ![]() is the
ideal gas constant.
is the
ideal gas constant.
An ideal monatomic gas molecule (negligible spin) has only
three degrees of freedom: its kinetic energy in the three spatial
dimensions. Therefore,
![]() . This means we expect
. This means we expect
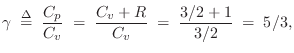
For an ideal diatomic gas molecule such as air, which can be pictured as a ``bar bell'' configuration of two rubber balls, two additional degrees of freedom are added, both associated with spinning the molecule about an axis orthogonal to the line connecting the atoms, and piercing its center of mass. There are two such axes. Spinning about the connecting axis is neglected because the moment of inertia is so much smaller in that case. Thus, for diatomic gases such as dry air, we expect
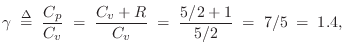
Speed of Sound in Air
The speed of sound in a gas depends primarily on the temperature, and can be estimated using the following formula from the kinetic theory of gases:B.33
Air Absorption
This section provides some further details regarding acoustic air
absorption [318]. For a plane wave, the decline of
acoustic intensity as a function of propagation distance ![]() is given
by
is given
by

Tables B.1 and B.2 (adapted from [314]) give some typical values for air.
| ||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
There is also a (weaker) dependence of air absorption on temperature [183].
Theoretical models of energy loss in a gas are developed in Morse and
Ingard [318, pp. 270-285]. Energy loss is caused by
viscosity, thermal diffusion, rotational
relaxation, vibration relaxation, and boundary losses
(losses due to heat conduction and viscosity at a wall or other
acoustic boundary). Boundary losses normally dominate by several
orders of magnitude, but in resonant modes, which have nodes along the
boundaries, interior losses dominate, especially for polyatomic gases
such as air.B.34 For air having moderate amounts of water
vapor (![]() ) and/or carbon dioxide (
) and/or carbon dioxide (![]() ), the loss and dispersion
due to
), the loss and dispersion
due to ![]() and
and ![]() vibration relaxation hysteresis becomes the
largest factor [318, p. 300]. The vibration here
is that of the molecule itself, accumulated over the course of many
collisions with other molecules. In this context, a diatomic molecule
may be modeled as two masses connected by an ideal spring. Energy
stored in molecular vibration typically dominates over that stored in
molecular rotation, for polyatomic gas molecules [318, p.
300]. Thus, vibration relaxation hysteresis is a loss
mechanism that converts wave energy into heat.
vibration relaxation hysteresis becomes the
largest factor [318, p. 300]. The vibration here
is that of the molecule itself, accumulated over the course of many
collisions with other molecules. In this context, a diatomic molecule
may be modeled as two masses connected by an ideal spring. Energy
stored in molecular vibration typically dominates over that stored in
molecular rotation, for polyatomic gas molecules [318, p.
300]. Thus, vibration relaxation hysteresis is a loss
mechanism that converts wave energy into heat.
In a resonant mode, the attenuation per wavelength due to vibration
relaxation is greatest when the sinusoidal period (of the resonance)
is equal to ![]() times the time-constant for vibration-relaxation.
The relaxation time-constant for oxygen is on the order of one
millisecond. The presence of water vapor (or other impurities)
decreases the vibration relaxation time, yielding loss maxima at
frequencies above 1000 rad/sec. The energy loss approaches zero as
the frequency goes to infinity (wavelength to zero).
times the time-constant for vibration-relaxation.
The relaxation time-constant for oxygen is on the order of one
millisecond. The presence of water vapor (or other impurities)
decreases the vibration relaxation time, yielding loss maxima at
frequencies above 1000 rad/sec. The energy loss approaches zero as
the frequency goes to infinity (wavelength to zero).
Under these conditions, the speed of sound is approximately that of dry air below the maximum-loss frequency, and somewhat higher above. Thus, the humidity level changes the dispersion cross-over frequency of the air in a resonant mode.
Next Section:
Wave Equation in Higher Dimensions
Previous Section:
Wave Equation for the Vibrating String