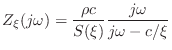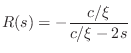DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Scattering Filters at the Cylinder-Cone Junction

As derived in §C.18.4, the wave impedance (for volume velocity) at frequency $ \omega $ rad/sec in a converging cone is given by

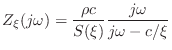$\displaystyle Z_\xi(j\omega) = \frac{\rho c}{S(\xi)} \frac{j\omega}{j\omega-c/\xi}$ (C.152)

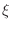
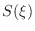
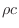
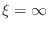
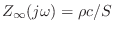
where $ \xi$ is the distance to the apex of the cone, $ S(\xi)$ is the cross-sectional area, and $ \rho c$ is the wave impedance in open air. A cylindrical tube is the special case $ \xi=\infty$, giving $ Z_\infty(j\omega) = \rho c/S$, independent of position in the tube. Under normal assumptions such as pressure continuity and flow conservation at the cylinder-cone junction (see, e.g., [300]), the junction reflection transfer function (reflectance) seen from the cylinder looking into the cone is derived to be

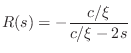$\displaystyle R(s) = -\frac{c/\xi}{c/\xi - 2s}$ (C.153)

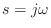
(where $ s$ is the Laplace transform variable which generalizes $ s=j\omega$) while the junction transmission transfer function (transmittance) to the right is given by

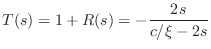$\displaystyle T(s) = 1 + R(s) = -\frac{2s}{c/\xi - 2s}$ (C.154)

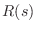
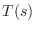
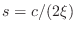
The reflectance and transmittance from the right of the junction are the same when there is no wavefront area discontinuity at the junction [300]. Both $ R(s)$ and $ T(s)$ are first-order transfer functions: They each have a single real pole at $ s=c/(2\xi)$. Since this pole is in the right-half plane, it corresponds to an unstable one-pole filter.

Next Section:
Reflectance of the Conical Cap
Previous Section:
Cylindrical Tubes