DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Conjugate Quadrature Filters (CQF)

A class of causal, FIR, two-channel, critically sampled, exact perfect-reconstruction filter-banks is the set of so-called Conjugate Quadrature Filters (CQF). In the z-domain, the CQF relationships are

$\displaystyle H_1(z) \eqsp z^{-(L-1)}H_0(-z^{-1}).$ (12.39)

In the time domain, the analysis and synthesis filters are given by

\begin{eqnarray*} h_1(n) &=& -(-1)^n h_0(L-1-n) \\ [5pt] f_0(n) &=& h_0(L-1-n) \\ [5pt] f_1(n) &=& -(-1)^n h_0(n) \eqsp - h_1(L-1-n). \end{eqnarray*}

That is, $ f_0=\hbox{\sc Flip}(h_0)$ for the lowpass channel, and each highpass channel filter is a modulation of its lowpass counterpart by $ (-1)^n$ . Again, all four analysis and synthesis filters are determined by the lowpass analysis filter $ H_0(z)$ . It can be shown that this is an orthogonal filter bank. The analysis filters $ H_0(z)$ and $ H_1(z)$ are power complementary, i.e.,

$\displaystyle \left\vert H_0{e^{j\omega}}\right\vert^2 + \left\vert H_1{e^{j\omega}}\right\vert^2 \eqsp 1$ (12.40)

or

$\displaystyle {\tilde H}_0(z) H_0(z) + {\tilde H}_1(z) H_1(z) \eqsp 1$ (12.41)

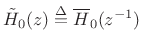where $ {\tilde H}_0(z)\isdef \overline{H}_0(z^{-1})$ denotes the paraconjugate of $ H_0(z)$ (for real filters $ H_0$ ). The paraconjugate is the analytic continuation of $ \overline{H_0(e^{j\omega})}$ from the unit circle to the $ z$ plane. Moreover, the analysis filters $ H_0(z)$ are power symmetric, e.g.,

$\displaystyle {\tilde H}_0(z) H_0(z) + {\tilde H}_0(-z) H_0(-z) \eqsp 1 .$ (12.42)

The power symmetric case was introduced by Smith and Barnwell in 1984 [272]. With the CQF constraints, (11.18) reduces to

$\displaystyle \hat{X}(z) \eqsp \frac{1}{2}\left[H_0(z)H_0(z^{-1}) + H_0(-z)H_0(-z^{-1})\right]X(z) \protect$ (12.43)

Let $ P(z) = H_0(z)H_0(-z)$ , such that $ H_0(z)$ is a spectral factor of the half-band filter $ P(z)$ (i.e., $ P(e^{j\omega})$ is a nonnegative power response which is lowpass, cutting off near $ \omega=\pi/4$ ). Then, (11.43) reduces to

$\displaystyle \hat{X}(z) \eqsp \frac{1}{2}\left[P(z) + P(-z)\right]X(z) \eqsp -z^{-(L-1)}X(z)$ (12.44)

The problem of PR filter design has thus been reduced to designing one half-band filter $ P(z)$ . It can be shown that any half-band filter can be written in the form $ p(2n) = \delta(n)$ . That is, all non-zero even-indexed values of $ p(n)$ are set to zero.

A simple design of an FIR half-band filter would be to window a sinc function:

$\displaystyle p(n) \eqsp \frac{\hbox{sin}[\pi n/2]}{\pi n/2}w(n)$ (12.45)

where $ w(n)$ is any suitable window, such as the Kaiser window.

Note that as a result of (11.43), the CQF filters are power complementary. That is, they satisfy

$\displaystyle \left\vert H_0(e^{j \omega})\right\vert^2 + \left\vert H_1(e^{j \omega})\right\vert^2 \eqsp 2.$ (12.46)

Also note that the filters $ H_0$ and $ H_1$ are not linear phase. It can be shown that there are no two-channel perfect reconstruction filter banks that have all three of the following characteristics (except for the Haar filters):
  • FIR
  • orthogonal
  • linear phase
In this design procedure, we have chosen to satisfy the first two and give up the third.

By relaxing ``orthogonality'' to ``biorthogonality'', it becomes possible to obtain FIR linear phase filters in a critically sampled, perfect reconstruction filter bank. (See §11.9.)

Next Section:
Orthogonal Two-Channel Filter Banks
Previous Section:
Linear Phase Quadrature Mirror Filter Banks