Iterated Convolutions

Free Books Spectral Audio Signal Processing

Any ``reasonable'' probability density function (PDF) (§C.1.3) has a Fourier transform that looks like $S(\omega) = 1 - \alpha \omega^2$ near its tip. Iterating convolutions then corresponds to $S^N(\omega)$ , which becomes [2]

$\displaystyle S^N(\omega) = (1-\alpha \omega^2)^N = \left(1-\frac{N\alpha \omega^2}{N}\right)^N \approx e^{-N\alpha\omega^2}$

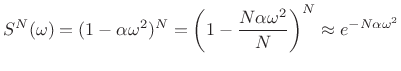(D.27)

for large , by the definition of [264]. This proves that the th power of $1-\alpha\omega^2$ approaches the Gaussian function defined in §D.1 for large .

Since the inverse Fourier transform of a Gaussian is another Gaussian (§D.8), we can define a time-domain function as being ``sufficiently regular'' when its Fourier transform approaches $S(\omega)\approx 1-\alpha\omega^2$ in a sufficiently small neighborhood of $\omega = 0$ . That is, the Fourier transform simply needs a ``sufficiently smooth peak'' at $\omega = 0$ that can be expanded into a convergent Taylor series. This obviously holds for the DTFT of any discrete-time window function (the subject of Chapter 3), because the window transform $W(\omega)$ is a finite sum of continuous cosines of the form $w(n)\cos(n\omega T)$ in the zero-phase case, and complex exponentials in the causal case, each of which is differentiable any number of times in $\omega$ .