Matlab for the Hann Window
In matlab, a length ![]() Hann window is designed by the statement
Hann window is designed by the statement
w = hanning(M);which, in Matlab only is equivalent to
w = .5*(1 - cos(2*pi*(1:M)'/(M+1)));For
>> hanning(3)
ans =
0.5
1
0.5
Note the curious use of M+1 in the denominator instead of
M as we would expect from the family definition in
(3.17). This perturbation serves to avoid using zero samples in
the window itself. (Why bother to multiply explicitly by zero?) Thus,
the Hann window as returned by Matlab hanning function
reaches zero one sample beyond the endpoints to the left and right.
The minus sign, which differs from (3.18), serves to make the
window causal instead of zero phase.
The Matlab Signal Processing Toolbox also includes a hann function which is defined to include the zeros at the window endpoints. For example,
>> hann(3)
ans =
0
1
0
This case is equivalent to the following matlab expression:w = .5*(1 - cos(2*pi*(0:M-1)'/(M-1)));The use of
In Matlab, both hann(3,'periodic') and hanning(3,'periodic') produce the following window:
>> hann(3,'periodic')
ans =
0
0.75
0.75
This case is equivalent to w = .5*(1 - cos(2*pi*(0:M-1)'/M));which agrees (finally) with definition (3.18). We see that in this case, the left zero endpoint is included in the window, while the one on the right lies one sample outside to the right. In general, the 'periodic' window option asks for a window that can be overlapped and added to itself at certain time displacements (
In Octave, both the hann and hanning functions include the endpoint zeros.
In practical applications, it is safest to write your own window functions in the matlab language in order to ensure portability and consistency. After all, they are typically only one line of code!
In comparing window properties below, we will speak of the Hann window
as having a main-lobe width equal to ![]() , and a side-lobe
width
, and a side-lobe
width ![]() , even though in practice they may really be
, even though in practice they may really be
![]() and
and
![]() , respectively, as illustrated
above. These remarks apply to all windows in the generalized Hamming
family, as well as the Blackman-Harris family introduced in
§3.3 below.
, respectively, as illustrated
above. These remarks apply to all windows in the generalized Hamming
family, as well as the Blackman-Harris family introduced in
§3.3 below.
Summary of Hann window properties:
- Main lobe is
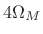 wide,
wide,
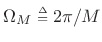
- First side lobe at -31dB
- Side lobes roll off approximately
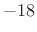 dB per octave
dB per octave
Next Section:
Hamming Window
Previous Section:
Hann or Hanning or Raised Cosine



















