Audio Spectrograms

Free Books Spectral Audio Signal Processing

Since classic spectrograms [132] typically show log-magnitude intensity (dB) versus time and frequency, and since sound-pressure level in dB is roughly proportional to perceived loudness, at least at high levels [179,276,305], we can say that a classic spectrogram provides a reasonably good psychoacoustic display for sound, provided the window length has been chosen to be comparable to the ``integration time'' of the ear.

However, there are several ways we can improve the classic spectrogram to obtain more psychoacoustically faithful displays of perceived loudness versus time and frequency:

Loudness perception is closer to linearly related to amplitude at low loudness levels.
Since the STFT offers only one ``integration time'' (the window length), it implements a uniform bandpass filter bank--i.e., spectral samples are uniformly spaced and correspond to equal bandwidths. The window transform gives the shape of each effective bandpass filter in the frequency domain. The choice of window length determines the common time- and frequency-resolution at all frequencies. Figure 9.14 shows a frequency-response overlay of all 5 channel filters created by a length 5 DFT using a zero-phase rectangular window.
In the ear, however, time resolution increases and frequency resolution decreases at higher frequencies. Thus, the ear implements a non-uniform filter bank, with wider bandwidths at higher frequencies. In the time domain, the integration time (effective ``window length'') becomes shorter at higher frequencies.

Auditory Filter Banks

Auditory filter banks are non-uniform bandpass filter banks designed to imitate the frequency resolution of human hearing [307,180,87,208,255]. Classical auditory filter banks include constant-Q filter banks such as the widely used third-octave filter bank. Digital constant-Q filter banks have also been developed for audio applications [29,30]. More recently, constant-Q filter banks for audio have been devised based on the wavelet transform, including the auditory wavelet filter bank [110]. Auditory filter banks have also been based more directly on psychoacoustic measurements, leading to approximations of the auditory filter frequency response in terms of a Gaussian function [205], a ``rounded exponential'' [207], and more recently the gammatone (or ``Patterson-Holdsworth'') filter bank [208,255]. The gamma-chirp filter bank further adds a level-dependent asymmetric correction to the basic gammatone channel frequency response, thus providing a more accurate approximation to the auditory frequency response [112,111].

The output power from an auditory filter bank at a particular time defines the so-called excitation pattern versus frequency at that time [87,179,305]. It may be considered analogous to the average power of the physical excitation applied to the hair cells of the inner ear by the vibrating basilar membrane in the cochlea.^8.6 The shape of the excitation pattern can thus be thought of as approximating the envelope of the basilar membrane vibration.

The excitation pattern produced from an auditory filter bank, together with appropriate equalization (frequency-dependent gain) and nonlinear compression, can be used to define specific loudness as a function of time and frequency [306,305,177,182,88].

Because the channels of an auditory filter bank are distributed non-uniformly versus frequency, they can be regarded as a basis for a non-uniform sampling of the frequency axis. In this point of view, the auditory-filter frequency response becomes the (frequency-dependent) interpolation kernel used to extract a frequency sample at the filter's center frequency. See §7.3.3 below for further details.

Loudness Spectrogram

The purpose of a loudness spectrogram is to display some psychoacoustic model of loudness versus time and frequency. Instead of specifying FFT window length and type, one specifies conditions of presentation, such as physical amplitude level in dB SPL, angle of arrival at the ears, etc. By default, it can be assumed that the signal is presented to both ears equally, and the listening level can be normalized to a ``comfortable'' value such as 70 dB SPL.^8.7

A time-varying model of loudness perception has been developed by Moore and Glasberg et al. [87,182,88]. A loudness spectrogram based on this work may consist of the following processing steps:

Compute a multiresolution STFT (MRSTFT) which approximates the frequency-dependent frequency and time resolution of the ear. Several FFTs of different lengths may be combined in such a way that time resolution is higher at high frequencies, and frequency resolution is higher at low frequencies, like in the ear. In each FFT, the frequency resolution must be greater than or equal to that of the ear in the frequency band it covers. (Even ``much greater'' is ok, since the resolution will be reduced down to what it should be by smoothing in Step 2.)
Form the excitation pattern from the MRSTFT by resampling the FFTs of the previous step using interpolation kernels shaped like auditory filters. The new spectral sampling intervals should be proportional to the width of a critical band of hearing at each frequency. The shape of each interpolation kernel (auditory filter) should change with amplitude level as well as center frequency [87]. This step effectively converts the uniform filter bank of the FFT to an auditory filter bank.^8.8
Compute the specific loudness from the excitation pattern for each frame. This step implements a compressive nonlinearity which depends on the frequency and level of the excitation pattern [182]. The specific loudness can be interpreted as loudness per ERB.
If desired, the instantaneous loudness can be computed as the the sum of the specific loudness over all frequency samples at a fixed time. Similarly, short- and long-term time-varying loudness estimates can be computed as lowpass-filterings of the instantaneous loudness over time [88].

The specific loudness gives a useful definition of the ``loudness spectrogram.'' However, one might well prefer to filter it across the time dimension in the same manner that instantaneous loudness is filtered to produce short- and long-term loudness estimates versus time and frequency.

A Note on Hop Size

Before Step 2 above, the FFT hop size within the MRSTFT of Step 1 would typically be determined by the shortest window length used (and its type). However, after the non-uniform downsampling in Step 2, the effective window lengths (and shapes) have been modified. If the spectrum is not undersampled by this operation, the effective duration of the time-domain window at each frequency will always be shorter than that of the original FFT window. In principle, the shape of the effective time-domain window becomes the product of the original FFT window used in the MRSTFT times the ``auditory window,'' which is given by the inverse Fourier transform of the auditory filter frequency response (spectral interpolation kernel) translated to zero center-frequency. (This is only approximately true when the auditory filter frequency response spans multiple frequency ranges for which FFTs were performed at different resolutions.)

Since the time-domain window durations are shortened by the spectral smoothing inherent in Step 2, the proper step size from frame to frame is something less than that dictated by the MRSTFT windows. One reliable method for determining the maximum allowable hop size for each FFT in the MRSTFT is to study the inverse Fourier transform of the widest (highest-frequency) auditory filter shape (translated to 0 Hz center-frequency) used as a smoothing kernel in that FFT. This new window can be multiplied by the original window and overlapped and added to itself, as in Eq. $\,$ (7.2), at various increasing hop-sizes (starting with which is always valid), until the overlap-add begins to show ripple at the frame rate . Alternatively, the bandwidth of the highest-frequency auditory filter can be used to determine the appropriate hop size in the time domain, as elaborated in Chapter 9 (especially §9.8.1).

Loudness Spectrogram Examples

We now illustrate a particular Matlab implementation of a loudness spectrogram developed by teaching assistant Patty Huang, following [87,182,88] with slight modifications.^8.9

Multiresolution STFT

Figure 7.4 shows a multiresolution STFT for the same speech signal that was analyzed to produce Fig.7.2. The bandlimits in Hz for the five combined FFTs were , where the last two (in parentheses) were not used due to the signal sampling rate being only kHz. The corresponding window lengths in milliseconds were , where, again, the last two are not needed for this example. Our hop size is chosen to be 1 ms, giving 75% overlap in the highest-frequency channel, and more overlap in lower-frequency channels. Thus, all frequency channels are oversampled along the time dimension. Since many frequency channels from each FFT will be combined via smoothing to form the ``excitation pattern'' (see next section), temporal oversampling is necessary in all channels to avoid uneven weighting of data in the time domain due to the hop size being too large for the shortened effective time-domain windows.

**Figure 7.4:** Multiresolution Short-Time Fourier Transform (MRSTFT). Compare to the fixed-resolution STFT in Fig.7.2.
$\includegraphics[width=\twidth]{eps/lsg-mrstft}$

Excitation Pattern

Figure 7.5 shows the result of converting the MRSTFT to an excitation pattern [87,182,108]. As mentioned above, this essentially converts the MRSTFT into a better approximation of an auditory filter bank by non-uniformly resampling the frequency axis using auditory interpolation kernels.

Note that the harmonics are now clearly visible only up to approximately 20 ERBs, and only the first four or five harmonics are visible during voiced segments. During voiced segments, the formant structure is especially clearly visible at about 25 ERBs. Also note that ``pitch pulses'' are visible as very thin, alternating, dark and light vertical stripes above 25 ERBs or so; the dark lines occur just after glottal closure, when the voiced-speech period has a strong peak in the time domain.

**Figure 7.5:** *Excitation pattern* versus time, computed from the MRSTFT.
$\includegraphics[width=\twidth]{eps/lsg-ep}$

Nonuniform Spectral Resampling

Recall sinc interpolation of a discrete-time signal [270]:

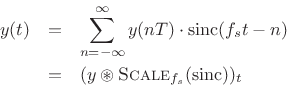
$\begin{eqnarray*} y(t) &=& \sum_{n=-\infty}^\infty y(nT)\cdot \mbox{sinc}(f_s t-n) \\ &=& (y \circledast \hbox{\sc Scale}_{f_s}(\mbox{sinc}))_t \end{eqnarray*}$

And recall asinc interpolation of a sampled spectrum (§2.5.2):

$\begin{eqnarray*} X(\omega) &=& \hbox{\sc DTFT}(\hbox{\sc ZeroPad}_{\infty}(\hbox{\sc IDFT}_N(X)))\\ &=& \sum_{k=0}^{N-1}X(\omega_k)\cdot \hbox{asinc}_N(\omega-\omega_k)\\ [5pt] &=& (X\circledast \hbox{asinc}_N)_\omega, \end{eqnarray*}$

We see that resampling consists of an inner-product between the given samples with a continuous interpolation kernel that is sampled where needed to satisfy the needs of the inner product operation. In the time domain, our interpolation kernel is a scaled sinc function, while in the frequency domain, it is an asinc function. The interpolation kernel can of course be horizontally scaled to alter bandwidth [270], or more generally reshaped to introduce a more general windowing in the opposite domain:

Width of interpolation kernel (main-lobe width) $\longleftrightarrow$ 1/width-in-other-domain
Shape of interpolation kernel $\longleftrightarrow$ gain profile (window) in other domain

Getting back to non-uniform resampling of audio spectra, we have that an auditory-filter frequency-response can be regarded as a frequency-dependent interpolation kernel for nonuniformly resampling the STFT frequency axis. In other words, an auditory filter bank may be implemented as a non-uniform resampling of the uniformly sampled frequency axis provided by an ordinary FFT, using the auditory filter shape as the interpolation kernel.

When the auditory filters vary systematically with frequency, there may be an equivalent non-uniform frequency-warping followed by a uniform sampling of the (warped) frequency axis. Thus, an alternative implementation of an auditory filter bank is to apply an FFT (implementing a uniform filter bank) to a signal having a properly prewarped spectrum, where the warping is designed to approximate whatever auditory frequency axis is desired. This approach is discussed further in Appendix E. (See also §2.5.2.)

Auditory Filter Shapes

The topic of auditory filter banks was introduced in §7.3.1 above. In this implementation, the auditory filters were synthesized from the Equivalent Rectangular Bandwidth (ERB) frequency scale, discussed in §E.5. The auditory filter-bank shapes are a function of level, so, ideally, the true physical amplitude level of the input signal at the ear(s) should be known. The auditory filter shape at 1 kHz in response to a sinusoidal excitation for a variety of amplitudes is shown in Fig.7.6.

**Figure 7.6:** Excitation patterns for a 1 kHz sinusoid at different levels.
$\includegraphics[width=4in]{eps/lsg-af}$

Specific Loudness

Figure 7.7 shows the specific loudness computed from the excitation pattern of Fig.7.5. As mentioned above, it is a compressive nonlinearity that depends on level and also frequency.

**Figure 7.7:** *Specific loudness* computed from the excitation pattern each time step.
$\includegraphics[width=\twidth]{eps/lsg-sl}$

Spectrograms Compared

Figure 7.8 shows all four previous spectrogram figures in a two-by-two matrix for ease of cross-reference.

**Figure 7.8:** (a) Classic spectrogram. (b) Multiresolution STFT dB magnitude. (c) Excitation pattern. (d) Specific loudness.
$\includegraphics[width=\twidth]{eps/lsg-fourcases}$

Instantaneous, Short-Term, and Long-Term Loudness

Finally, Fig.7.9 shows the instantaneous loudness, short-term loudness, and long-term loudness functions overlaid, for the same speech sample used in the previous plots. These are all single-valued functions of time which indicate the relative loudness of the signal on different time scales. See [88] for further discussion. While the lower plot looks reasonable, the upper plot (in sones) predicts only three audible time regions. Evidently, it corresponds to a very low listening level.^8.10

The instantaneous loudness is simply the sum of the specific loudness over all frequencies. The short- and long-term loudnesses are derived by smoothing the instantaneous loudness with respect to time using various psychoacoustically motivated time constants [88]. The smoothing is nonlinear because the loudness tracks a rising amplitude very quickly, while decaying with a slower time constant.^8.11 The loudness of a brief sound is taken to be the local maximum of the short-term loudness curve. The long-term loudness is related to loudness memory over time.

The upper plot gives loudness in sones, which is based on loudness perception experiments [276]; at 1 kHz and above, loudness perception is approximately logarithmic above 50 dB SPL or so, while below that, it tends toward being more linear. The lower plot is given in phons, which is simply sound pressure level (SPL) in dB at 1 kHz [276, p. 111]; at other frequencies, the amplitude in phons is defined by following an ``equal-loudness curve'' over to 1 kHz and reading off the level there in dB SPL. This means, e.g., that all pure tones have the same perceived loudness when they are at the same phon level, and the dB SPL at 1 kHz defines the loudness of such tones in phons.

**Figure 7.9:** Total *instantaneous*, *short-term*, and *long-term* loudness, computed from the specific loudness. Top: *sone* loudness scale. Bottom: loudness in *phons*.
$\includegraphics[width=4in]{eps/lsg-isl}$

Next Section:
Summary
Previous Section:
Classic Spectrograms