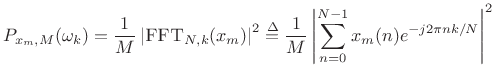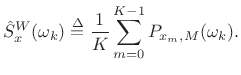Free Books
   Free Books    Spectral Audio Signal Processing  

Welch's Method

Welch's method [296] (also called the periodogram method) for estimating power spectra is carried out by dividing the time signal into successive blocks, forming the periodogram for each block, and averaging.

Denote the $ m$ th windowed, zero-padded frame from the signal $ x$ by

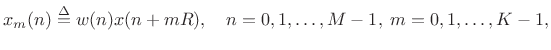$\displaystyle x_m(n)\isdef w(n)x(n+mR), \quad n=0,1,\ldots,M-1,\; m=0,1,\ldots,K-1,$ (7.26)

where $ R$ is defined as the window hop size, and let $ K$ denote the number of available frames. Then the periodogram of the $ m$ th block is given by

$\displaystyle P_{x_m,M}(\omega_k) = \frac{1}{M}\left\vert\hbox{\sc FFT}_{N,k}(x_m)\right\vert^2 \isdef \frac{1}{M}\left\vert\sum_{n=0}^{N-1} x_m(n) e^{-j2\pi nk/N}\right\vert^2 \protect$

as before, and the Welch estimate of the power spectral density is given by

$\displaystyle {\hat S}_x^W(\omega_k) \isdef \frac{1}{K}\sum_{m=0}^{K-1}P_{x_m,M}(\omega_k). \protect$ (7.27)

In other words, it's just an average of periodograms across time. When $ w(n)$ is the rectangular window, the periodograms are formed from non-overlapping successive blocks of data. For other window types, the analysis frames typically overlap, as discussed further in §6.13 below.

Welch Autocorrelation Estimate

Since $ \left\vert X_m\right\vert^2\;\longleftrightarrow\;x\star x$ which is circular (or cyclic) correlation, we must use zero padding in each FFT in order to be able to compute the acyclic autocorrelation function as the inverse DFT of the Welch PSD estimate. There is no need to arrange the zero padding in zero-phase form, since all phase information is discarded when the magnitude squared operation is performed in the frequency domain.

The Welch autocorrelation estimate is biased. That is, as discussed in §6.6, it converges as $ K\to\infty$ to the true autocorrelation $ r_x(l)$ weighted by $ M-\vert l\vert$ (a Bartlett window). The bias can be removed by simply dividing it out, as in (6.15).

Resolution versus Stability

A fundamental trade-off exists in Welch's method between spectral resolution and statistical stability. As discussed in §5.4.1, we wish to maximize the block size $ M$ in order to maximize spectral resolution. On the other hand, more blocks (larger $ K$ ) gives more averaging and hence greater spectral stability. A typical default choice is $ M\approx K\approx \sqrt{N_x}$ , where $ N_x$ denotes the number of available data samples.

Next Section:
Welch's Method with Windows
Previous Section:
The Periodogram