DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

The Running-Sum Lowpass Filter

Perhaps the simplest FIR lowpass filter is the so-called running-sum lowpass filter [175]. The impulse response of the length $ N$ running-sum lowpass filter is given by

$\displaystyle h(n) \isdef \left\{\begin{array}{ll} 1, & n=0,1,2,...,N-1 \\ [5pt] 0, & \hbox{otherwise.} \\ \end{array} \right. \protect$ (10.5)

Figure 9.10: Black-box view of application of the running-sum lowpass filter.
\includegraphics{eps/blackbox}

Figure 9.10 depicts the generic operation of filtering $ x(n)$ by $ h(n)$ to produce $ y(n)$ , where $ h(n)$ is the impulse response of the filter. The output signal is given by the convolution of $ x$ and $ h$ :

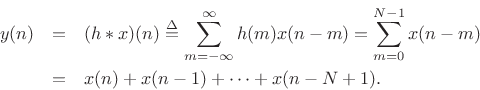
\begin{eqnarray*} y(n) &=& (h\ast x)(n) \isdef \sum_{m=-\infty}^{\infty} h(m) x(n-m) = \sum_{m=0}^{N-1} x(n-m)\\ &=& x(n) + x(n-1) + \cdots + x(n-N+1). \end{eqnarray*}

In this form, it is clear why the filter (9.5) is called ``running sum'' filter. Dividing it by $ N$ , it becomes a ``moving average'' filter, averaging the most recent $ N$ input samples.

The transfer function of the running-sum filter is given by [263]

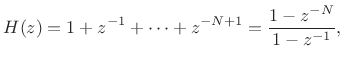$\displaystyle H(z) = 1 + z^{-1}+ \cdots + z^{-N+1} = \frac{1-z^{-N}}{1-z^{-1}},$ (10.6)

so that its frequency response is

\begin{eqnarray*} H(e^{j\omega}) &=& \frac{1-e^{-j\omega N}}{1-e^{-j\omega }} = \frac{e^{-j\omega N/2}}{e^{-j\omega /2}} \frac{\sin(\omega N/2)}{\sin(\omega /2)}\\ [10pt] &\isdef & Ne^{-j\omega(N-1)/2} \hbox{asinc}_N(\omega ). \end{eqnarray*}

Recall that the term $ e^{-j\omega(N-1)/2}$ is a linear phase term corresponding to a delay of $ (N-1)/2$ samples (half of the FIR filter order). This arises because we defined the running-sum lowpass filter as a causal, linear phase filter.

We encountered the ``aliased sinc function''

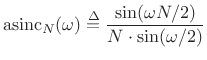$\displaystyle \hbox{asinc}_N(\omega ) \isdef \frac{\sin(\omega N/2)}{N\cdot\sin(\omega /2)}$ (10.7)

previously in Chapter 5 (§3.1.2) and elsewhere as the Fourier transform (DTFT) of a sampled rectangular pulse (or rectangular window).

Note that the dc gain of the length $ N$ running sum filter is $ N$ . We could use a moving average instead of a running sum ( $ h \leftarrow h/N$ ) to obtain unity dc gain.

Figure: Running-sum amplitude response for $ N=5$
\includegraphics[width=4in]{eps/sincabs}

Figure 9.11 shows the amplitude response of the running-sum lowpass filter for length $ N=5$ . The gain at dc is $ N=5$ , and nulls occur at $ \omega = \pm2\pi/5$ and $ \pm4\pi/5$ . These nulls occur at the sinusoidal frequencies having respectively one and two periods under the 5-sample ``rectangular window''. (Three periods would need at least $ 2\cdot 3 = 6$ samples, so $ 6\pi/5$ doesn't ``fit''.) Since the pass-band about dc is not flat, it is better to call this a ``dc-pass filter'' rather than a ``lowpass filter.'' We could also call it a dc sampling filter.10.1

Next Section:
Modulation by a Complex Sinusoid
Previous Section:
Computational Examples in Matlab