DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

The STFT as a Time-Frequency Distribution

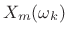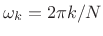The Short Time Fourier Transform (STFT) $ X_m(\omega_k)$ is a function of both time (frame number $ m$ ) and frequency ( $ \omega_k = 2\pi k/N$ ). It is therefore an example of a time-frequency distribution. Others include

The uniform and rectangular nature of the STFT time-frequency tiling is illustrated in Fig.7.1. The window length is proportional to the resolution cell in time, indicated by the vertical lines in Fig.7.1. The width of the main-lobe of the window-transform is proportional to the resolution cell in frequency, indicated by the horizontal lines in Fig.7.1. As detailed in Chapter 3, choosing a window length $ M$ and window type (Hamming, Blackman, etc.) chooses the ``aspect ratio'' and total area of the time-frequency resolution cells (rectangles in Fig.7.1). For an example of a non-uniform time-frequency tiling, see Fig.10.14.

Figure: Example time-frequency tiling for the STFT. Vertical line spacing indicates time resolution, and horizontal line spacing indicates frequency resolution (both fixed by window length and type). The area of the rectangular cells are bounded below by the minimum time-bandwidth product (see §B.17.1 for one definition).
\includegraphics[width=0.8\twidth]{eps/timefreq}

Next Section:
STFT in Matlab
Previous Section:
Two Dual Interpretations of the STFT