Canonic Signed Digit (CSD) Representation of Integers
In my last post I presented Matlab code to synthesize multiplierless FIR filters using Canonic Signed Digit (CSD) coefficients. I included a function dec2csd1.m (repeated here in Appendix A) to convert decimal integers to binary CSD values. Here I want to use that function to illustrate a few properties of CSD numbers.
In a binary signed-digit number system, we allow each binary digit to have one of the three values {0, 1, -1}. Thus, for example, the binary value 1 1 1 1 1 (decimal 31) could be written as the signed-digit value
1 0 0 0 0 -1 = 25 - 20 = d31. The reduction of non-zero digits in this scheme allows replacing full multipliers with ones using shifts and adds, resulting in more efficient implementations of FIR filters.
The Canonic Signed Digit representation requires that no adjacent digits are nonzero. That is, the combinations 1 1; -1 1; 1 -1; or -1 -1 do not occur. As an example, we can look at the CSD values for the integers 1 to 10 using dec2csd1.m:
nbits= 4; % number of bits integers= 1:10; Y= dec2csd1(integers,nbits); % matrix of binary CSD values B = fliplr(Y) % flip to put MSB on left
The resulting CSD representation of integers 1, 2, … 10 is:
B =
0 0 0 1
0 0 1 0
0 1 0 -1
0 1 0 0
0 1 0 1
1 0 -1 0
1 0 0 -1
1 0 0 0
1 0 0 1
1 0 1 0
As you can see, the number of signed digits (nsd) for each integer value is either 1 or 2. For integer = 7, the CSD version uses 2 nonzero digits, compared to 3 nonzero digits for straight binary.
CSD Properties
No adjacent digits are nonzero
See example above for integers from 1 to 10.
Negative integers
To implement a negative integer, just compute the CSD value of the positive integer and invert the sign of each digit.
Largest value vs. number of bits (nbits)
The largest CSD value is 101010… This approaches 2/3* 2nbits for nbits large. For example, if nbits= 8, the maximum value is 10101010 = 170. 170/28 = 0.664. Nine bits are needed to represent a number greater than 170.
Maximum number of signed digits vs nbits
nsd_max = nbits/2, nbits even
= (nbits+1)/2, nbits odd
Table 1. CSD properties vs. nbits
| nbits | max value | max value (dec) | nsd_max |
| 4 | 1010 | 10 | 2 |
| 8 | 10101010 | 170 | 4 |
| 9 | 101010101 | 341 | 5 |
| 10 | 1010101010 | 682 | 5 |
| 11 | 10101010101 | 1365 | 6 |
| 12 | 101010101010 | 2730 | 6 |
Distribution of signed digits
As shown above, nsd_max depends on the number of bits. We can also look at the distribution of the number of signed digits for different values of nbits. The m-file in Appendix B computes nsd for every integer for a given value of nbits and plots them. Figure 1 shows the distribution of nsd for nbits = 8, along with a histogram of the occurrences of each nsd value. Figures 2 – 4 show the distributions for nbits = 9, 10, and 11.
Multiplierless FIR Filters Using CSD Coefficients
CSD filters are area and power efficient and can operate at high sample rates. In designing a filter, the stopband requirement determines nbits, which in turn determines the number of signed digits. We wish to minimize nsd. If, for example, we choose nbits = 9, then nsd_max = 5, but this value occurs only 16 times (see Figure 2). So it should typically be possible to synthesize a filter with 9-bit coefficients using four or fewer signed digits per coefficient. Some methods of avoiding higher nsd values are as follows:
1. Scale the coefficient amplitudes, choosing a scaling that minimizes nsd. This is the method used in my previous post on multiplierless FIR filters.
2. Use the approach above, then replace any coefficients bi with value nsd_max as follows: bi_new = bi + 1 or bi -1. By definition, the new value will have nsd < nsd_max. Then compare the frequency response to the response using the original CSD coefficient value.
3. Perform a search over coefficients with lower values of nsd, and optimize the coefficient values vs. a frequency response objective function. This approach is more complicated than the first two, but can achieve more efficient designs.
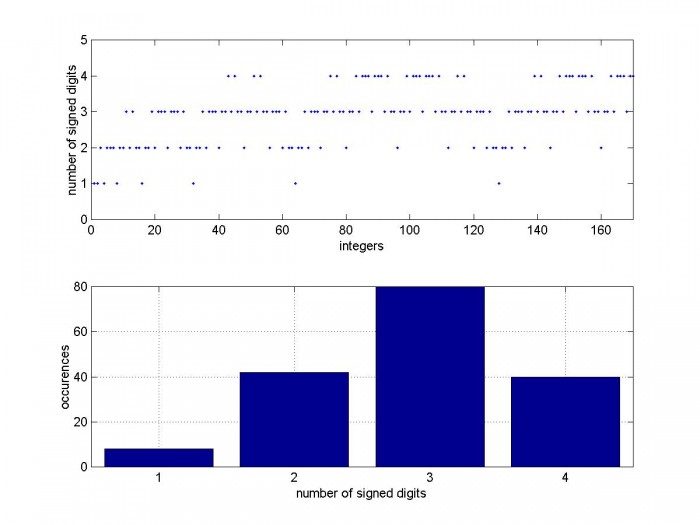
Fig 1. Top: Number of signed digits vs CSD value, nbits = 8
Bottom: Histogram of nsd
note: max CSD value for nbits = 8 is 170.
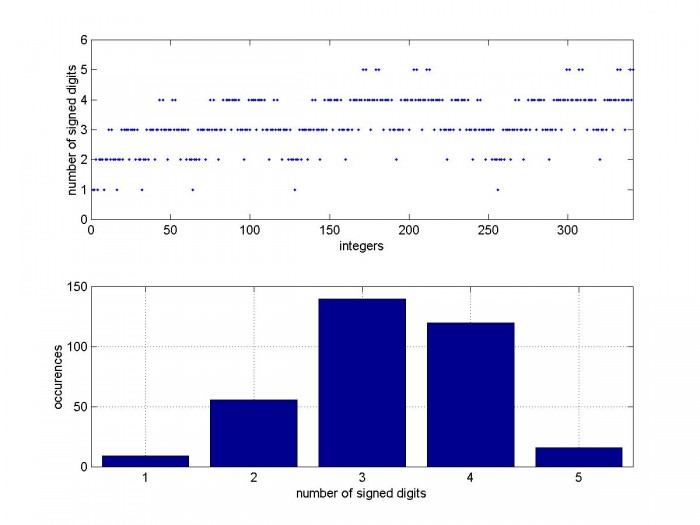
Fig 2. Top: Number of signed digits vs CSD value, nbits = 9
Bottom: Histogram of nsd
note: max CSD value for nbits = 9 is 341.
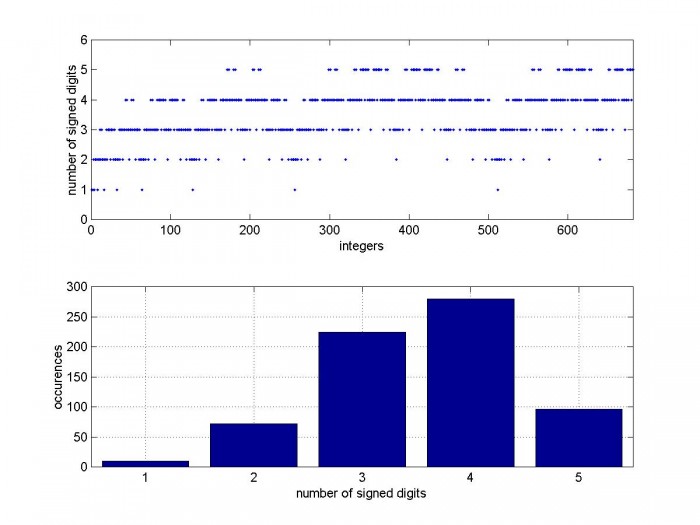
Fig 3. Top: Number of signed digits vs CSD value, nbits = 10
Bottom: Histogram of nsd
note: max CSD value for nbits = 10 is 682.
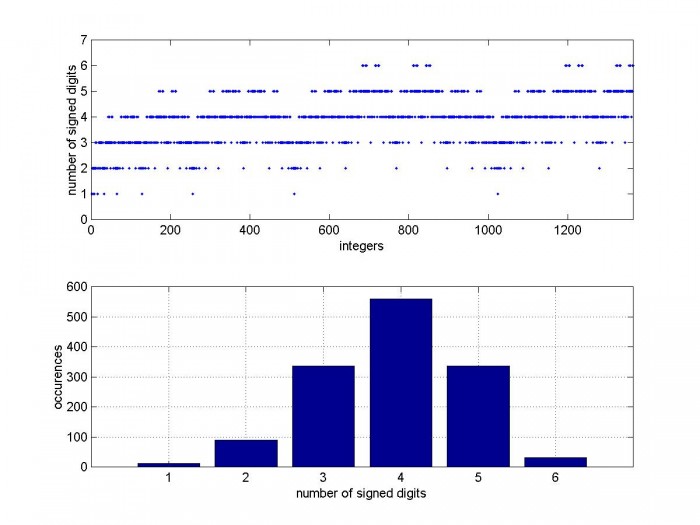
Fig 4. Top: Number of signed digits vs CSD value, nbits = 11
Bottom: Histogram of nsd
note: max CSD value for nbits = 11 is 1365.
Reference
Ruiz and Granda, "Efficient Canonic Signed Digit Recoding", Microelectronics Journal 42, p 1090-1097, 2011
Appendix A. Matlab Function to convert decimal integers to binary CSD numbers
This programs is provided as-is without any guarantees or warranty. The author is not responsible for any damage or losses of any kind caused by the use or misuse of the program.
% Y= dec2csd1(b_int,nbits) 10/25/16 Neil Robertson
% Convert signed decimal integers to binary CSD representation
% See Ruiz and Granda, "Efficient Canonic Signed Digit Recoding",
% Microelectronics Journal 42, p 1090-1097, 2011
%
% b_int = vector of decimal integer coefficients
% nbits = number of bits in b_int coeffs
% Y = matrix of CSD coeffs
% A = matrix of binary coeffs
%
% -- j= 1:nbits --
% _ _
% | ---- coeff 1 ---- |
% | ---- coeff 2 ---- |
% | . . . |
% Y,A = | ---- coeff i ---- |
% | . . . |
% | -- coeff ntaps -- |
% - -
%
% 1. convert decimal integers to binary integers
function Y= dec2csd1(b_int,nbits)
ntaps= length(b_int); % number of coeffs
for i= 1:ntaps % coeff index (row index)
u= abs(b_int(i));
for j= 1:nbits % binary digit index (column index)
A(i,j)= mod(u,2); % coeff magnitudes note: MSB is on right.
u= fix(u/2);
end
end
% 2. convert binary integers to CSD
s= sign(b_int); % signs of coeffs
z= zeros(ntaps,1);
x= [A z]; % MSB is on right. append 0 as MSB
for i= 1:ntaps % coeff index (row index)
c= 0;
for j= 1:nbits % binary digit index (column index)
d= xor(x(i,j),c);
ys= x(i,j+1)&d; % sign bit 0 == pos, 1 == negative
yd= ~x(i,j+1)&d; % data bit
Y(i,j)= yd - ys; % signed digit
c_next = (x(i,j)&x(i,j+1)) | ((x(i,j)|x(i,j+1))&c); % carry
c= c_next;
end
Y(i,:) = Y(i,:)*s(i); % multiply CSD coeff magnitude by coeff sign
end
Appendix B. m-file to plot distribution of number of signed digits
%csd_plot.m Neil Robertson 2/16/17
% convert integers to CSD and plot number of signed digits
clear
nbits= 8; % number of bits
N= fix(2/3*2^nbits); % largest integer is <= largest CSD value = 101010...
integers= 1:N;
Y= dec2csd1(integers,nbits); % matrix of binary CSD values
for i= 1:N
nsd(i)= sum(abs(Y(i,:))); % number of signed digits in Y(i)
end
nsd_max= max(nsd); % max number of signed digits
subplot(211),plot(integers,nsd,'.')
axis([0 N 0 nsd_max+1])
xlabel('integers'),ylabel('number of signed digits')
for i= 1:nsd_max;
total(i)= length(find(nsd == i)); % occurances of nsd = 1, nsd = 2, ...
end
subplot(212),bar([1:nsd_max],total),grid
xlabel('number of signed digits')
ylabel('occurrences')
- Comments
- Write a Comment Select to add a comment
To post reply to a comment, click on the 'reply' button attached to each comment. To post a new comment (not a reply to a comment) check out the 'Write a Comment' tab at the top of the comments.
Please login (on the right) if you already have an account on this platform.
Otherwise, please use this form to register (free) an join one of the largest online community for Electrical/Embedded/DSP/FPGA/ML engineers:



















