ADC Clock Jitter Model, Part 1 – Deterministic Jitter

• Matlab
• Tutorials

Analog to digital converters (ADC’s) have several imperfections that affect communications signals, including thermal noise, differential nonlinearity, and sample clock jitter [1, 2].  As shown in Figure 1, the ADC has a sample/hold function that is clocked by a sample clock.  Jitter on the sample clock causes the sampling instants to vary from the ideal sample time.  This transfers the jitter from the sample clock to the input signal.

In this article, I present a Matlab ADC jitter model.  The model’s inputs are an arbitrary ADC input signal vector and a time-jitter vector.  The input signal can be a sine, multiple sines or anything you want to try.  The time jitter can be sine, Gaussian, filtered-Gaussian, etc.  The model is useful in giving a sense of how input signals and their spectra are affected by jitter, which we’ll see in some examples.

Random jitter, or phase noise, is inherent in any oscillator.  In the frequency domain, it appears as a spreading of the carrier energy that is referred to as sidebands, but these sidebands are not discrete.  Deterministic jitter is caused by real-world implementations where, for example, unwanted clock signals may be coupled to power or ground traces of the sample clock oscillator, causing discrete phase sidebands.   Since the discrete jitter case is simplest, we’ll begin with it here in Part 1.  Then we’ll cover random jitter in Part 2.

This article is available in PDF format for easy printing.

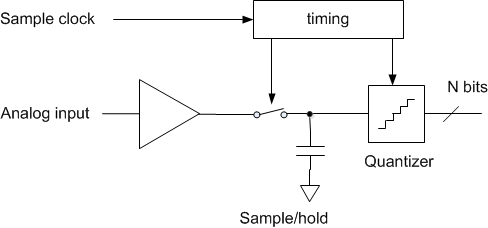
Figure 1.  Sample clock and ADC sample/hold function

Example 1.

The Matlab function adc_jitter is listed in the appendix.  Before describing how the function works, we’ll use it to perform a simulation using a sine input and sinusoidal jitter on the sample clock.

We have to create the analog input signal and the time jitter vector before we call adc_jitter.  First, we define the ADC sample rate, input signal frequency, jitter frequency, and jitter amplitude.  Also, we define the simulation sample rate, which is twice the ADC sample rate.

    fs_adc= 100E6;             % Hz ADC sample rate
    f0 = 10E6;                 % Hz ADC input sinewave frequency
    fm = 1.9E6;                % Hz jitter freq
    A = 200e-12;               % s peak jitter of sample clock
    fs= 2*fs_adc;              % Hz simulation sample rate

Next, define the analog input sinewave x and the jitter sinewave dt.  The units of the jitter amplitude is seconds.  We compute the jitter in samples = dt/Ts, then call the Matlab function adc_jitter.  Finally, we quantize the output to 10 bits.

    Ts= 1/fs;                        % s sample time
    N= 4096;
    n= 0:N-1;                        %  sample index
    x= sin(2*pi*f0*n*Ts);            %  adc analog input
    dt= A*cos(2*pi*fm*n*Ts);         % s sinusoidal jitter of sample clock
    dsample= dt/Ts;                  %  jitter in samples
    y= adc_jitter(x,dsample);        %  add jitter to x
    nbits= 10;
    y= floor(2^(nbits-1)*y)/2^(nbits-1);    % quantize to nbits

The output y is at the fs_adc sample rate of 100 MHz.  An eye diagram superimposing all cycles of the ADC output sinewave is plotted in Figure 2.  The jitter is just visible.  A zoomed version is shown in Figure 3.  The jitter is equal to that of the sample clock, i.e. 200 ps peak or 400 ps peak-to-peak.

The spectra of the ADC input and output are shown in Figure 4.  The input spectrum is a pure tone.  The output spectrum has sidebands due to sample clock jitter at f_m= 1.9 MHz.  You can also see the quantization noise floor at the bottom edge of the plot.

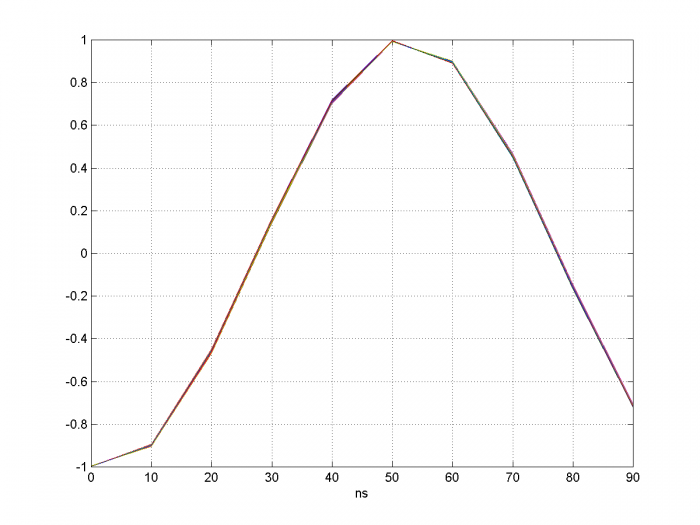
Figure 2.  Eye Diagram with time axis showing one cycle of ADC output signal.

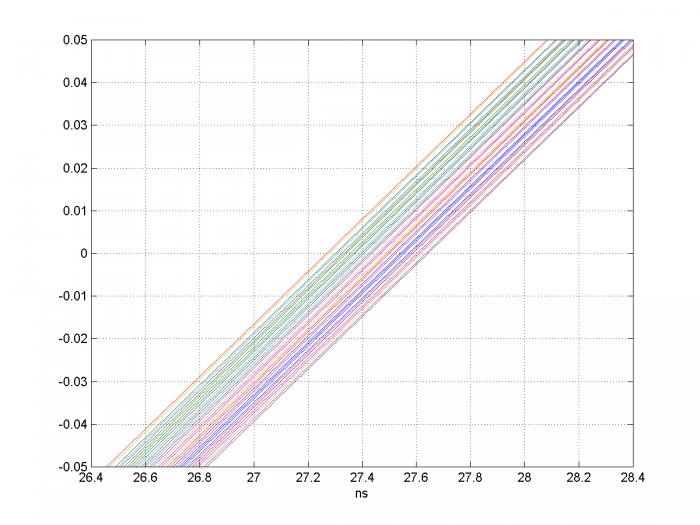
Figure 3.  Zoom of Eye Diagram at 200 ps per division.

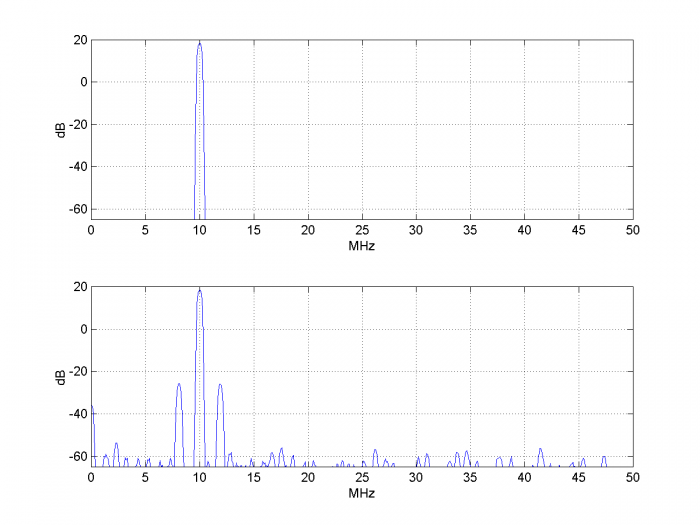
Figure 4.Top:  Spectrum of ADC input signal.

Bottom:  Spectrum of ADC output signal  psd(y,N/4,fs_adc/1e6,flattopwin(N/4))

How the Model Works

The Matlab function adc_jitter(x,dsample) is shown in the appendix.  The function’s inputs are the ADC analog input x(n) and the sample clock jitter in samples, dsample(n).

In Example 1, we assumed a time jitter waveform dt(n) that was a sinusoid with frequency f_m and amplitude A seconds.  For every sample n, we had dt(n) = A*cos(2πf_m*nT_s).  We then computed jitter in samples as dsample(n) = dt(n)/T_s.

Thus, for every ADC sample x(n), the sampling instant was offset by dt(n).  As shown in Figure 5 for a single sample, this time offset means that the sampled analog voltage is offset from the ideal value.  The model needs to estimate this voltage, shown as the red asterisk.  It does so by interpolating between samples of the input voltage. We need to use a variable interpolator because each value of dt(n) is unique; i.e., the interpolation index dt(n)/T_s is not a constant.

Since we are normally interested in small values of dt, we could use a linear interpolator.  However, we can get more accurate results over a wider range of jitter amplitude by using a polynomial (e.g. parabolic or cubic) interpolator [3, 4].  The function adc_jitter uses parabolic interpolation.

Referring again to Figure 5, note that if the input signal is sinusoidal, the jitter dt moves the sample point in phase by 2π* dt/T_s.  Thus the jitter on the sample clock amounts to phase modulation of the input sinusoid.  To the extent that our model’s interpolation is accurate, it performs pure phase modulation.

A few details:  First, the inputs x and dsample of adc_jitter are sampled at twice the ADC sample rate of fs_adc.  Once the interpolated values are calculated, they are downsampled by two, to fs_adc.  The reason for this is to account for the bandwidth of the interpolator (see appendix).  Input signal frequency components above fs_adc/2 will be aliased.  Second, rather than using interpolation index of dt/T_s, we use dt/T_s + 0.5.  This prevents having a negative interpolation index when dt is negative.  Finally, note that in all of this we did not generate a sample clock; the model doesn’t need a sample clock, just the vector dsample of jitter in samples.

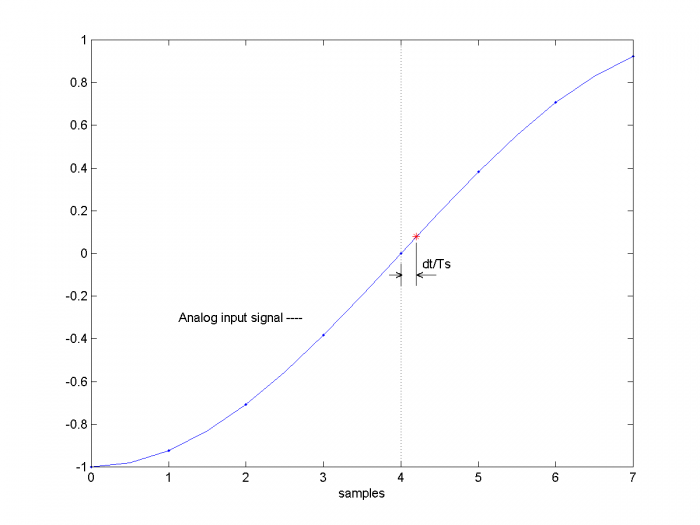
Figure 5.  Effect of jitter on sampling

Calculating Sidebands Caused by Jitter

One way to check the model is to calculate the jitter sidebands and see if the model matches the calculation.  We begin by noting that the jitter sidebands represent phase modulation.  We then have [5]:

$$\phi^2=\frac{2\cdot SSB\, power}{carrier\, power}\qquad rad^2$$

where ϕ is rms phase relative to carrier phase in radians and SSB power is the power of one sideband.  We can rewrite the above as:

$$\phi^2=2\cdot 10^{PSSB/10} \; ,$$

where PSSB is the power of one sideband in dB relative to the carrier power (dBc).  We have assumed the level of higher-order phase sidebands is negligible.  Taking the square-root,

$$\phi= \sqrt{2} \cdot 10^{PSSB/20}\qquad rad\;rms$$

Thus,

$$PSSB = 20log_{10}(\phi)-3.01\qquad dBc \qquad (1)$$

Phase jitter in radians and clock jitter in seconds are simply related by:

$$\phi=2\pi \frac{\Delta t_{rms}}{T_0}=2\pi\Delta t_{rms}f_0 \qquad (2) $$

where Δt_rms is the rms clock jitter in seconds, T₀ is carrier period, and f₀ is carrier frequency.  For an ADC, the jitter Δt_rms in Equation 2 is a constant vs. f₀.  Thus for increasing f₀, Δt_rms becomes a larger and larger fraction of T₀, causing ϕ to grow linearly vs. f₀.  Substituting for ϕ in equation 1, we have:

$$PSSB = 20log_{10}(2\pi\Delta t_{rms}f_0) -3.01\qquad dBc \qquad (3)$$

Example 1 used $\Delta t_{rms}= 200/\sqrt{2} $ ps and f₀ = 10 MHz, so we expect PSSB = -44.04 dB.  Checking Figure 4, we see good agreement.

We can also relate the ADC output’s sideband level directly to the sideband level of the sample clock.  For the sample clock, we can modify Equation 3 as follows, where we use the fact that the jitter on the carrier and the sample clock are both Δt_rms:

$$PSSB_{clk} = 20log_{10}(2\pi\Delta t_{rms}f_s) -3.01\qquad dBc $$

Combining this with Equation 2, we then have:

$$PSSB_{signal}= PSSB_{clk} -20log_{10} (f_s/f_0) \qquad (4)$$

In other words, the signal sidebands are lower than the sample clock sidebands by $20log_{10}(f_s/f_0) $ dB.

Example 2.

Equation 3 shows that the sideband level due to jitter varies as 20*log₁₀ of the analog input signal’s carrier frequency.  We can illustrate this by letting the input equal the sum of two sinewaves at 10 MHz and 40 MHz.  Then the sideband level should be 20*log₁₀(4) = 12 dB higher at 40 MHz than at 10 MHz.  We use the same code as above, with ADC input x replaced by:

    x= sin(2*pi*f0*n*Ts) + sin(2*pi*4*f0*n*Ts);    % adc analog input

The resulting input and output spectra are shown in Figure 6.  As expected, the sidebands at 40 MHz are about 12 dB higher than those at 10 MHz.  The second-order phase sidebands are also visible.  Note that the input signal amplitude is about +/-2 V_pp, so quantization level is effectively 11 bits.

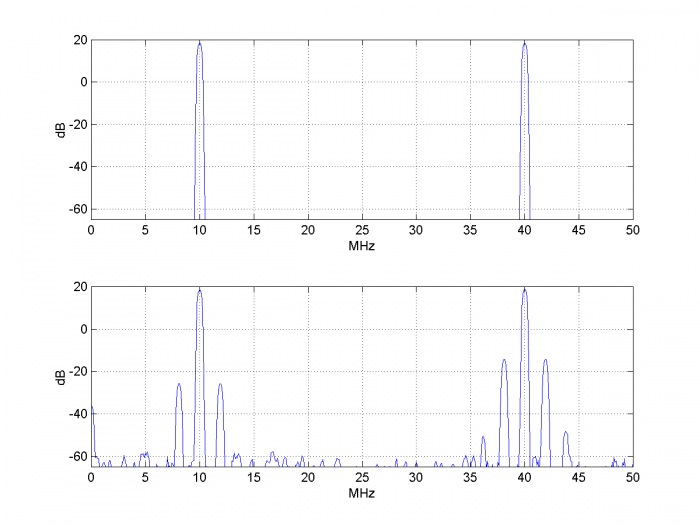
Figure 6.Top:  Spectrum of ADC input signal.    Bottom:  Spectrum of ADC output signal

Example 3.

In this example, we’ll phase-demodulate the ADC output, and compare the demodulated phase jitter to the expected jitter.  We set the input frequency and jitter as follows:

    f0 = 35E6;        % Hz ADC input sinewave frequency
    A= 0.6e-9         % s  peak jitter of sample clock

This gives the spectrum of Figure 7.  Now let’s calculate the expected phase jitter of the output.Modifying Equation 2 for peak-to-peak phase jitter, we have:

$$\phi_{pp}=2\pi\Delta t_{pp}f_0 $$

So we expect ϕ_pp = 2π*1.2E-9*35E6 = .2639 radians pp or 15.12 degrees pp.  If we phase-demodulate the ADC output and plot Q vs. I, we get the result shown in Figure 8.  As expected, the peak-to-peak phase jitter is about 15 degrees.  It is worth noting that even for the relatively large phase excursion of this example, the model produces almost pure phase modulation on the ADC output.

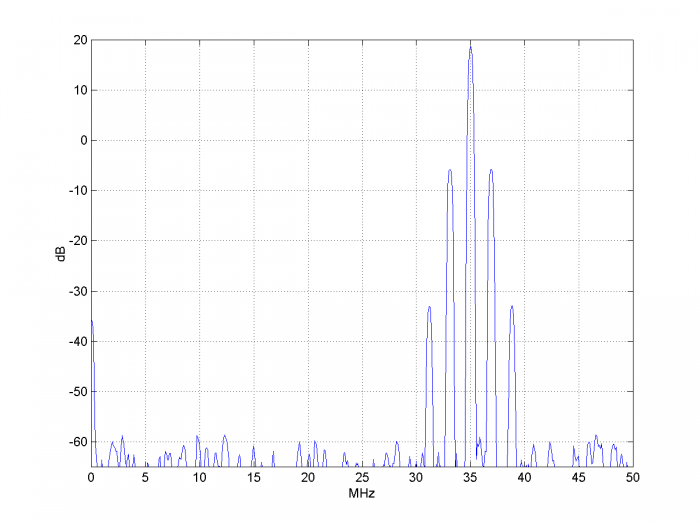
Figure 7.  Spectrum of ADC output for f0 = 35 MHz and sample clock peak jitter = 0.6E-9 s.

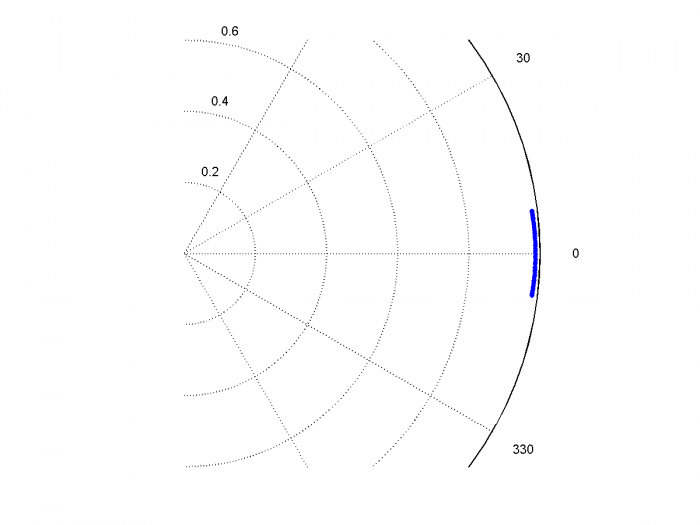
Figure 8.  Q vs. I of phase-demodulated ADC output signal for f0 = 35 MHz

and sample clock peak jitter = 0.6E-9 s.

Example 4.

We can also model a non-sinusoidal input to the ADC.  Figure 9 shows the spectrum of a modulated pulse with approximately rectangular spectrum applied to the ADC, where we have set:

    f0 = 30E6;        % Hz ADC input center frequency
    fm= 3.9E6;        % Hz jitter freq
    A= 100e-12        % s peak jitter of sample clock

The ADC output has jitter sidebands offset from the signal by +/- f_m = +/- 3.9 MHz.

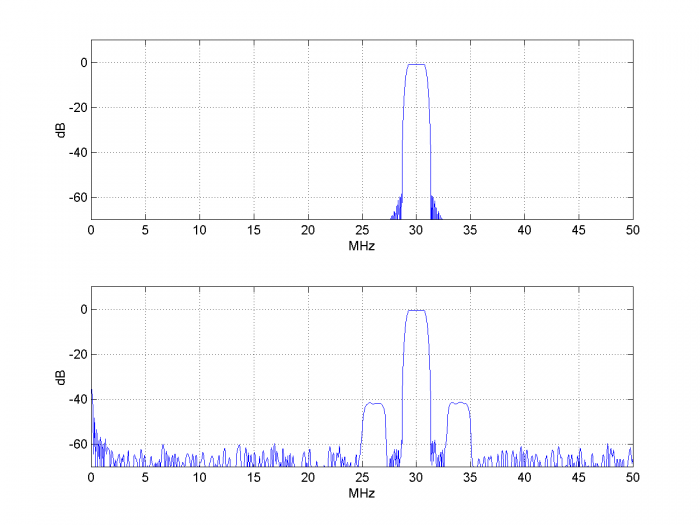
Figure 9.  Top:  Spectrum of ADC input signal.      Bottom:  Spectrum of ADC output signal.

References

1.  Kester, Walt, Ed., The Data Conversion Handbook, 2005, Newnes, Ch 2.

http://www.analog.com/en/education/education-library/data-conversion-handbook.html

2.  Brannon, Brad, “Sampled Systems and the Effects of Clock Phase Noise and Jitter”, Analog Devices Application Note AN-756, 2004

http://www.analog.com/media/en/technical-documentation/application-notes/AN-756.pdf

3.  Erup, Lars; Gardner, Floyd M. and Harris, Robert A., “Interpolation in Digital Modems – Part II:Implementation and Performance”, IEEE Transactions on Communications, Vol 41, No. 6, June 1993.

4.  Rice, Michael, Digital Communications, a Discrete-Time Approach, Pearson Prentice Hall, 2009, section 8.4.2.

5.  Goldberg, Bar-Giora, “Phase Noise Theory and Measurements:A Short Review”, Microwave Journal, Jan 1 2000.  https://www.google.com/search?q=%2C+Phase+Noise+Theory+and+Measurements%3A+A+Short+Review&oq=%2C+Phase+Noise+Theory+and+Measurements%3A+A+Short+Review&aqs=chrome..69i57.4669j0j8&sourceid=chrome&ie=UTF-8

Neil Robertson       April, 2018

Revised March 2019

Appendix   Matlab Function adc_jitter

Figure A.1 shows the interpolation of the input signal about mu = 0.5 + dt/Ts = 0.5 + dsample, where dsample is signed.  Figure A.2 shows the frequency response of the interpolator for mu = 0.5.  Because the output is downsampled by two, only the frequency range from 0 to fs/4 is used.

%function y= adc_jitter(x,dsample)  4/15/18  Neil Robertson
% Model ADC with jitter on sample clock, computing jittered samples by
% parabolic interpolation.
% Add jitter to input signal x, then downsample by 2.
%
% x          input signal vector
% dsample    input jitter vector, jitter in samples
% y          output signal vector with jitter, sample freq = 1/2 of input fs
%
function y= adc_jitter(x,dsample)
if length(x)~=length(dsample)
    error('x and dsample must be of equal length')
end
N= length(x);
V= x;
% find jittered samples using parabolic interpolation
mu= 0.5 + dsample;                % mu = 0.5 +/- jitter
a= 0.4;                           % interpolator free parameter
b1= [-a a+1 a-1 -a];              % Farrow coefficients
b2= [1 -1 -1 1];                  % Farrow coefficients
u= zeros(1,N);
for n= 4:N;
     Vreg= V(n:-1:n-3);        % reg holding 4 samples of V, current sample first
     u(n)= Vreg(3) + mu(n)*( sum(b1.*Vreg) + mu(n)*a*sum(b2.*Vreg));
end
y= u(1:2:end);                    % downsample by 2

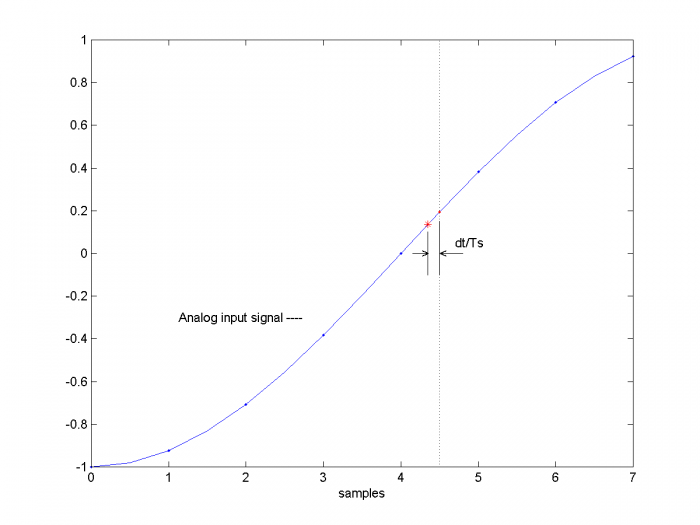
Figure A.1  Variable Interpolation.  mu= 0.5 + dt/Ts = 0.5 + dsample.

(example with dt/Ts negative)

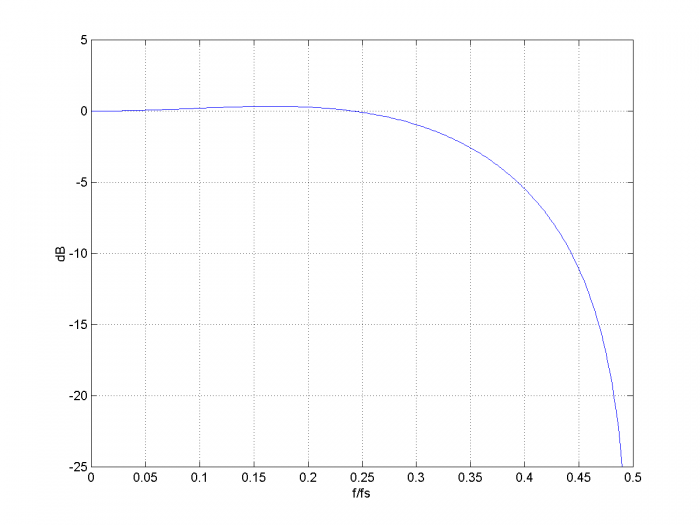
Figure A.2  Parabolic Interpolator Frequency response for mu = 0.5 and a = 0.4.

Sign in