Why stop there? Why not go on to the hyper reals? I.e the structure in which infinitesimal exis.

Hello LM741. I'm not familiar with hyper reals. Also, I'm afraid that if I study those numbers I will experience hypertension.

Hi Rick,
The interesting idea behind the oval diagrams is that one can form a closure of the number system behind with successively stronger notions of closure. ‘The Reals’ are what we get when we ‘closure under cuts’, the hypereals are what you get when you get with ‘closure under infinitesimals’. The advantage of the hyperreals is that one can use infinitesimals rigorously in mathematical arguments rather than argue by limits. A simple introduction is “Infinitesimal Calculus” by Henle & Kleinberg (Dover edition) - hyperreals without hypertension!

You forgot the distinctions around zero.
Some number systems have no zero, such as Roman numerals (and no negative).
We also have the subtle distinction between additive (difference) zero and multiplicative (presence/absence) zero.
Then there are the infinitesimal zeros (for every distinct infinity it needs a reciprocal..). Many issues regarding Noise & Phase arise from the countable/uncountable distinction for sampled signals ("Alias Free Sampling of Random Noise").
Even without 'Answers' (about Zero) the realisation that there can be Issues will help to understand why & when approximations fail (see wave-particle duality, etc.).
Thankfully we don't have to consider economics where negative numbers (debt) has a different scale factor (interest rate) compared to the positive numbers.
The diagram is useful for highlighting the step to algebraic "Solve(Sum(A.n * x^n)=0)", and beyond

Nice!
What got you thinking about the various types of numbers?

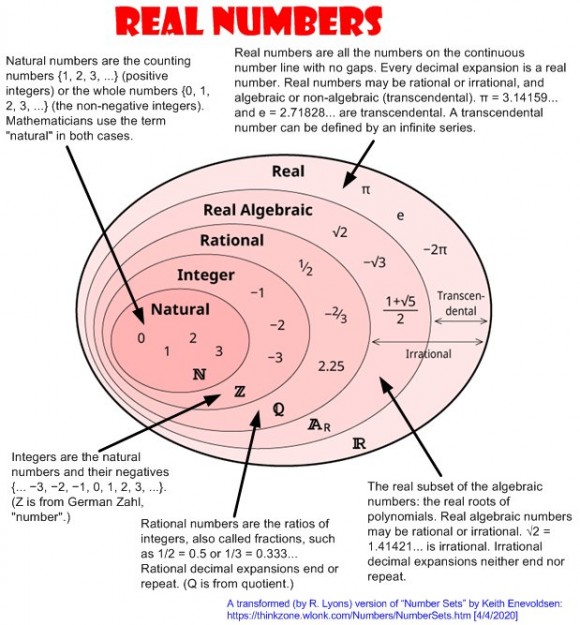
Hi Jason (jms_nh). I don't recall what caused me to visit Keith Enevoldsen's web site. I liked his "embedded ovals" diagram. So I copied that diagram, used his text, and added the arrows to combine his "numbers' information into a single graphic that I could print out in pin to my office wall.

Rick,
I like it too. But what about lucky numbers and unlucky numbers? I think they are a subset of the integers.
-- Neil

Hi Neil. Good idea. How about this:


It's fun to see when you get mathy.
I'm in the camp that considers zero distinct from the Natural numbers. I don't think the leap to having the concept of zero should be swept under the rug so easily by failing to note this distinction.
Leaving that aside, what about the next big step that is glaringly missing, the complex numbers?
Ced
P.S. Are 0.999999999..... and 1.000000.... distinct?

Sure they are distinct.
I'd guess it's easy to prove that 0.9999... is always less than 1.0000...
Bernhard

Hi Cedron. I'm pretty sure I understand what the number zero means. But I'm not confident that I fully understand what infinity means.
I vaguely recall several years ago seeing a proof (that seemed valid to me at the time) leading mathematicians to generally consider 0.99999... to be equal to one. But I don't recall that proof off the top of my head. I'll see if I can relocate that proof.
OK, five minutes later I found one proof that 0.99999... is equal to one. Here it is:

The "weak link in the chain" of the above proof may be the statement that:
10n = 9.99999...
I wonder if 10n really is equal to 9.99999... .
If the above proof is valid, then that proof also implies that 9.99999... is equal to 10. Now if 9.99999... is equal to 10 then is 3.99999... equal to 4?

This simple proof implies that it is allowed to multiply a number with infinite decimals and that multiplication result has equal number of decimals. I'm not sure if this is a legal assumption.
Another approach (maybe it's enough to be a proof) is that you can define the distance between 0.9 and 1.0 which is 0.1, then proceed with adding one digit and show that the difference is 0.01, having decreased.
Thus you can decrease the difference below any value, which means that lim(diff)->0, so they have to be equal.
In the same way you can prove it with 3.999... and 4 or whatever.

Hi bholzmayer. Thanks for your interesting thoughts!

They are not distinct. The dots represent a limit argument and the limit of both is the same value. Thus decimal representations of numbers are not necessarily unique.
You both touch on the limit argument. Rick's "proof" is the geometric sum series. The only thing missing was to state that the ratio of terms has to be less than one for the series to converge. Bernhard's second approach is the classic Epsilon definition of convergence of a sequence. "Given any Epsilon > 0, there exists an N such that for all n > N, | Sn - L | < Epsilon".
This is all part of the branch of math known as Real Analysis, that arose out to the study of the ability of the Fourier series to converge to a discontinuous function.
Ced

Hi Cedron. Regarding the proof I copied from the Internet and posted here, you wrote: "Rick's "proof" is the geometric sum series. The only thing missing was
to state that the ratio of terms has to be less than one for the series
to converge." I don't see a "geometric series" nor a "ratio of terms" in that proof.

0.9999999... = 9 * ( 0.111111111... )
Where r = 0.1 < 1 so it converges.
So you did the "multiply by 'r' trick"
S_N = 1 + r + r^2 + .... + r^(N-1)
r * S_N = r + r^2 + r^3 + ... + r^N
r * S_N - S_N = r^N - 1
Hence
S_N = (1-r^N) / (1-r)
It is clear to see if |r| < 1 this converges to 1/(1-r), and if |r| > 1 it diverges as N goes to infinity.
To do in properly, you sum up to N, and then let N approach infinity as a limit.
Real Analysis is the math where you can no longer count on your intuition and have to prove things rigorously. I have to wait to watch Bernhard's video reference, but I also have a counter example the seems to indicate that 0.9999... and 1.0000... are distinct.
-------------------------------------
Any repeating decimal sequence represents a convergent infinite geometric series.
For example:
x = 0.456456456......
1000x = 456.456456456....
999x = 456
x = 456/999 = 152/333

But if this is meant to be a counter example then do exactly the same with .999... and you get 1, so where’s the counter example?

I'm sorry, that wasn't the counter example.
It starts with "Is it possible to make a continuous mapping from R onto R^2?"

I've posted it below.

When reading this again, a good illustration came to my mind.
If you think of the function f(x)=1/x and another g(x)=-1/x.
They have certainly the same limit for increasing x.
But there's always the x-axis between both curves...
And, f(x) is always positive, while g(x) is always negative.
So: they have the same limit, but are the curves "hitting" or "touching" each other somewhere??

I remember reading a book about the life of Georg Cantor who was dealing with infinity in number theory (Aleph etc.).
The author of the book stated that quite a number of famous mathematicians who tried to understand infinity got crazy and some ended up in psychiatry.
So be aware of too much interest in this area - it seems to be a dangerous ground...

0.999999... and 1.00000... never "touch" each other, and are always distinct, yet their limits are the same.
I had not realy heard of the hyperreals before. My impression after a little bit of looking into it is that it is a different equivalent description of the same math. Having alternative paradigms for the same math is very common. Math is discovered, you have no choice in how it works, but the symbology to encapsulate it understandably has to be invented. Often, more than one version is useful. For instance, the "infinistismal" expression of the first derivative is in dy/dx form, and the functional representation f'(x), are both convenient (and more meaningful) in various contexts. In my math classes "infinistisimals" were considered a "creative fiction" and only treated informally.
Now, getting back to R onto R^2, consider the following. Suppose I map every real to a pair of reals by taking every other decimal of their infinite expansions.
(0.12345679...) --> ( 0.1357.., 0.2468.. )
This will map the interval (0,1) to the open unit square, and will be continuous. So, in this case, what happens to 0.099999999999999 vs 0.1000000000?
They seem to map to (.0999999999, 0.99999999) and ( 0.100000000000, 0.000000000 ) respectively. Suppose we call this one-to-one mapping F. We now have the case where the continuous function of two variables diverges while the variables themselves converge.
Definitely enough to drive you insane if you are the type who likes things tied in neat little packages.

Hi Cedron,
Do you think this mapping by picking decimals does really make sense with respect to comparing numbers? To point out the issue:
why not start with the zero before the '.' and use the '.' only in the second number?? I would doubt if this is really a good idea.
But it remembers me to a mathematician, I guess it was Georg Cantor again, who used a related idea (diagonal argument) based on natural numbers to prove that rational numbers are a countable set while real numbers aren't.

To address your particular concern. The mapping can be extended to the whole line covering the whole plane. When you take every other digit, the decimal point falls where it does. One value is going to get the tenths digit, and the other the hundredth, and so on. The order of the two values is independent of the strange features so we can throw a big WLOG (without loss of generality) on it.
Does it make sense that "there are the same number of" (cardinality) of rational numbers as integers? Does it make sense that there are (countably) infinitely many rational numbers between any two distinct reals? Or that there are an (uncountable) infinite number of reals between any two distince rationals? (including between every partial sum of 0.9999... and 1.0000... to infinity, and beyond?? ;-) )
These were my least favorite math classes, by far. Still, this example does take you to the edge of what the meaning of continuity really is and sort of has the "Gee whiz, that's something to think about" quality that I think Rick is striving for when he posts these things.

I had not such math classes - not in school and not during my studies - maybe bc. we were trained with the Electronics/Physics focus. What a pity...
Only later I stumbled about these "philosphical" issues of mathematics - and I digged into some of these issues just for fun :-))
In my practical work I had to learn that quantizations of infinitesimalities are quite often crucial and it matters, if a demodulated signal crosses zero at the same time for I and Q or in subsequent samples.
These are the moments where infinite resolution would be so much desirable, while I'm missing the target because of these odd real world deviations from perfect theory.
So it just feels good to let my brains enjoy surfing on such theory waves every now and then.
That's one of my reasons to follow this forum ...

I think your path is actually better. This is material that is best contemplated/learned by being interest driven and tangent permitting. Having a few more orbits around the orb that blinds doesn't hurt either says he who is just a couple behind you.

In essence you are confusing two different notions - the number and the representation of the number. 0.999999... and 0.100000 are different representations of the same real number. This simply means that your function is ill defined e.g. taking the odd digits of a decimal expansion is only a well defined function if the representation as a decimal expansion is unique, which the limit argument shows not to be the case. Nice argument but not a counter example

See the "seems"? (Should have been "that seems" not "the seems", sorry.)
To be technically precise, your statement "are different representations of the same real number." is incomplete and inaccurate. They represent two different series, each having a sequence of partial sums, that converge to the same limit. I think I have hashed out the details sufficiently in my other posts.
Yes, it is a neat example which is why it has stuck with me nearly forty years later. It is not "ill defined", but tremendously profound. No, there is no utilitarian value as far as I can tell.
"On a hill in Scotland, there is a sheep which has at least one side black ..... "

Here is a much simpler example to understand how the function values of two converging sequences can diverge.
Suppose f(x) = 1/x and you have two sequences a_n and b_n that both converge to zero. Now, suppose a_n is always less than zero and b_n is greater than zero. In this example you also have the case where two domain values are converging, but the function values are divergent.
The primary difference in this example though is the function 1/x is not continuous. In the decimal expansion example, the "discontinuity" has sort of been pushed off to infinity as well.

With reference to ‘seems’: In an earlier reply to me you referred to a ‘counter example’ posted below, which strongly suggests that you intend this to be taken as a counter example.
On my reply: The statement that they are two different representations of the same real number is neither inaccurate nor incomplete. A representation of a real number as a sequence of digits to some base is how we commonly deal with number. For example we may represent th winter also [0,1] using base 2 expansions rather than base 10, or base, or base 34. All have the property that certain real numbers have multiple representation in the given base. A function is a function on the reals if it gives the same answer on all representations of the reals, in contrast with functions on representations on reals.
Now let’s tidy up the maths a bit.
The general idea about what is going on is that we have a particular ‘algebra’ of representation which is syntax and an algebra which is semantics and a homomorphism between the tho taking syntax to semantics. Syntax is usually taken to be a free algebra and this this case the semantic algebra is the real field.
Since we are dealing with syntax that includes infinite sequences alluded to by ellipses we need to deal with the difference between finite sequences and infinite sequences. Rather than bore you with a whole load of tools we will simple take the syntactic algebra to be functions from natural numbers to digits in the appropriate base. Finite numbers are represented as functions which always yield the zero digit after some natural number n. The interpretation of a representation (syntax) is a homomorphism into the algebra of the reals so in the case of decimal representations d1d2d3... the interpretation is given by the map d1/10 + d2/100 + d2/1000 ...
In general we have for representations in base b, with digits 0 to b-1, the interpretation map
d1d2d3... |—> Sigma_i d_i/b^i
or more precisely
f |—> Sigma_i f(i)/b^i
where f is the function which is a particular representation of a number.
Of course, we could choose other structures for syntax as long as we can define the required homomorphism to interpret the structure.
Your argument is nice in the sense that many fallacious arguments in mathematics are nice (see e.g. Maxwell’s Fallacies in Mathematics). It is not profound, just a misunderstanding.

Again, this example comes from my Real Analysis class. The prof didn't call it a fallacy, nor treat it like a fallacy. It was an example to demonstrate that when it comes to dealing with infinity(ies), one has to be extremely rigorous. I took this stuff so long ago, and haven't really used it since, so I don't feel comfortable arguing the nuances of the definitions. The context of the example was the challenge to continuously map a line segment onto a square, R -> R^2. The emphasis was on the definition of continuity. I can understand your point about a function not giving two values for the same input value, and this one doesn't, until the limit "is reached", which never happens.
Interesting, uncomfortable, and counterintuitive, but not fallacious, particularly not in sense of a "hidden divide by zero" or "multivalued functions (okay, relations)" with the wrong values used.

Another issue which you have to ponder with...
Real numbers is a "complete" set of numbers, and it does not contain infinity.
If so, how many digits can a number like 9.999... contain?
If not infinitely many, hence it cannot be the same as 10.000...
I guess a century ago, NonStandardAnalysis extended the range of
numbers by placing between every real number and its neighbour, so-called hyperreal numbers.
German Prof. Dr. Edmund Weitz (HAW Hamburg) made a youtube video which started with the question of a school girl asking the question of the equality between 9.9999... and 10.0000...
It's very interestingly dealing with a huge bunch of number theory - but it's German.
He mentions two authors (Schmieden, Laugwitz) which prove that both numbers are NOT equal.
This is the link of the video:
Ist 0,999... wirklich 1? (Das Rätsel des Kontinuums)

In all my 67 years, I had never realised the importance of the number 6174.
Life will never be the same again . . .

I agree. There's nothing beyond. Almost.
Since Douglas Adams' The Hitchhiker's Guide to the Galaxy
revealed the prime elements of its magic, its obvious.
But you'll certainly agree, that 88942644 is topping it.
It uses the same prime elements, but watch the exponents!
And: I'm only 61, and already found it!!!

1*2*3*7 = 42
(1^0)*(2^1)*(3^2)*(7^3) = 6174
(1^1)*(2^2)*(3^3)*(7^7) = 88942644

https://www.quantamagazine.org/the-octonion-math-t...
From the "Final Theory" section, my intuition agrees, there is probably a discrete formulation, which is the path I am pursuing with my work on the Eigenvectors of the DFT.
I had heard about quarternions before, but this is my first exposure to octonions (and sedenions and beyond!)
This stuff is a lot more enjoyable to study when you aren't going to be tested on it. ;-)