Hello!

From here, they had derived the difference equation of a second-order DF-II structure.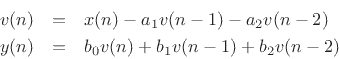 

How did they derive these equations from the given structure?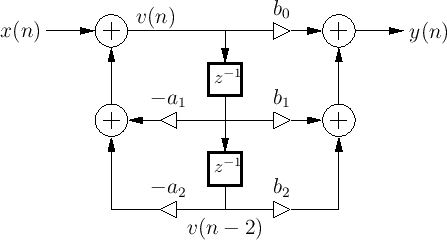

Did they use z-transform and converted it into the difference equation? What is the mathematical process into doing this?

Thanks.

To add to the good replies... 

It also might be helpful intuitively to look at Direct Form I and see how it translates to Direct Form II.

Given a 2nd order filter...

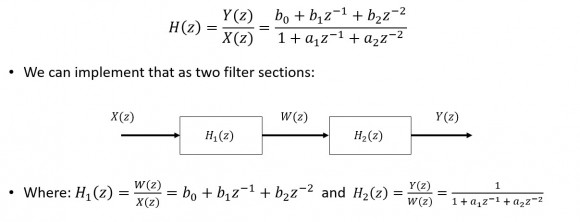
Here is the first section...

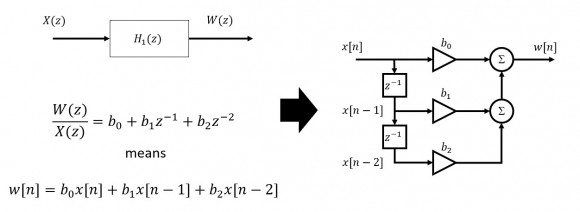
...and the second section...

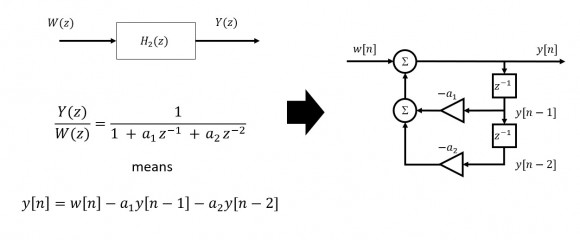
...combining we get Direct Form I.

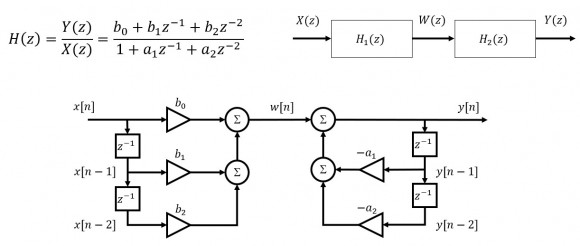
Since H1(z)H2(z)=H2(z)H1(z), we can swap the sections...

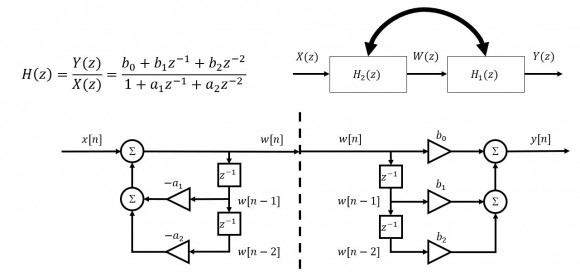
With the swap, we end up with a redundant center:

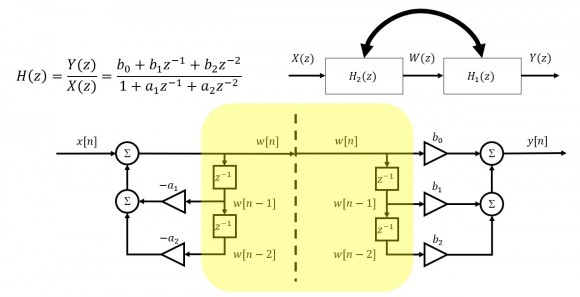
...and commonizing that delay line yields Direct Form II as you depicted above.

First of all you need to know:

the block z^-1 is a delay in n. That's the basic knowledge you need to have by analyzing these blocksets with respect to Z-transform.

example:

v(n) * z^-1 = v(n-1)

v(n) * z^-1 * z^-1 = v(n) * z^-2 = v(n-2)

The triangles are gains. The left one in the middle "-a1" has to be multiplied in line and sum up with the other lines.

Picking the first equation, you start with the sum symbol on the left side, where every path has to be added and the path beyond and so on.

focus on sum object and solve the equation step by step ;-).

transfer function

Y(Z)/X(Z) = [b0 + b1 Z^(-1) + b2 Z^(-2)]/[1 + a1 Z^(-1) +a2 Z^(-2)]

add internal variable W(Z)

[Y(Z)/(X(Z)] {W(Z)/W(Z)] =[Y(Z)/W(Z)] [W(Z)/X(Z)]

where [W(Z)/X(Z)] = 1/[1 + a1 Z^(-1) +a2 Z^(-2)]

and Y(Z)/W(Z) = [(b0 + b1 Z^(-1) + b2 Z^(-2)]

fred

By examination, you can see that the two components making up v(n), i.e. arrows into the summing point, are the input x(n) with the sum of:

1) product of -a1 and the delayed version of v(n), or v(n-1).  The z^-1 in the box is a delay element, so when it gets to -a1 it is v(n-1)

2) product of -a2 and double delayed version of v(n), or v(n-2), since there are two delay elements from v(n)

1) and 2) are summed together, at the + circle and then added to the incoming v(n), giving the first equation.

Similar logic/examination for the y(n), i.e. summation of the product of b0, b1, and b2 by v(n), delayed v(n) and doubly delayed version of v(n) respectively.

Robert