DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Low and High Shelving Filters

The analog transfer function for a low shelf is given by [103]

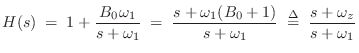
$\displaystyle H(s) \;=\; 1 + \frac{B_0\omega_1}{s+\omega_1} \;=\; \frac{s+\omega_1(B_0+1)}{s+\omega_1} \;\isdef \; \frac{s+\omega_z}{s+\omega_1} $

where $ B_0$ is the dc boost amount (at $ s=0$), and the high-frequency gain ($ s=\infty$) is constrained to be $ 1$. The transition frequency dividing low and high frequency regions is $ \omega_1$. See Appendix E for a development of $ s$-plane analysis of analog (continuous-time) filters.

A high shelf is obtained from a low shelf by the conformal mapping $ s \leftarrow 1/s$, which interchanges high and low frequencies, i.e.,

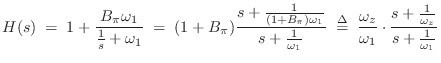
$\displaystyle H(s) \;=\; 1 + \frac{B_\pi\omega_1}{\frac{1}{s}+\omega_1} \;=\; ... ...{\omega_z}{\omega_1} \cdot \frac{s + \frac{1}{\omega_z}}{s+\frac{1}{\omega_1}} $

In this case, the dc gain is 1 and the high-frequency gain approaches $ 1+B_\pi = \omega_z/\omega_1$.

To convert these analog-filter transfer functions to digital form, we apply the bilinear transform:

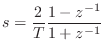
$\displaystyle s = \frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}} $

where $ T$ denotes the sampling interval in seconds.B.5

Low and high shelf filters are typically implemented in series, and are typically used to give a little boost or cut at the extreme low or high end (of the spectrum), respectively. To provide a boost or cut near other frequencies, it is necessary to go to (at least) a second-order section, often called a ``peaking equalizer,'' as described in §B.5 below.

Exercise

Perform the bilinear transform defined above and calculate the coefficients of a first-order digital low shelving filter. Find the pole and zero as a function of $ B_0$, $ \omega_1$, and $ T$. Set $ z = 1$ and verify that you get a gain of $ 1+B_0$. Set $ z = -1$ and verify that you get a gain of 1 there.

Next Section:
Peaking Equalizers
Previous Section:
DC Blocker