DC Blocker
The dc blocker is an indispensable tool in digital waveguide modeling [86] and other applications.B.4 It is often needed to remove the dc component of the signal circulating in a delay-line loop. It is also often an important tool in multi-track recording, where dc components in the various tracks can add up and overflow the mix.
The dc blocker is a small recursive filter specified by the difference equation
Thus, there is a zero at dc (
DC Blocker Frequency Response
Figure B.11 shows the frequency response of the dc blocker
for several values of ![]() . The same plots are given over a
log-frequency scale in Fig.B.12. The corresponding
pole-zero diagrams are shown in Fig.B.13. As
. The same plots are given over a
log-frequency scale in Fig.B.12. The corresponding
pole-zero diagrams are shown in Fig.B.13. As ![]() approaches
approaches
![]() , the notch at dc gets narrower and narrower. While this may seem
ideal, there is a drawback, as shown in Fig.B.14 for the
case of
, the notch at dc gets narrower and narrower. While this may seem
ideal, there is a drawback, as shown in Fig.B.14 for the
case of ![]() : The impulse response duration increases as
: The impulse response duration increases as ![]() .
While the ``tail'' of the impulse response lengthens as
.
While the ``tail'' of the impulse response lengthens as ![]() approaches
1, its initial magnitude decreases. At the limit,
approaches
1, its initial magnitude decreases. At the limit, ![]() , the pole and
zero cancel at all frequencies, the impulse response becomes an
impulse, and the notch disappears.
, the pole and
zero cancel at all frequencies, the impulse response becomes an
impulse, and the notch disappears.
![\includegraphics[width=\twidth ]{eps/dcblockerfr}](http://www.dsprelated.com/josimages_new/filters/img1459.png) |
![\includegraphics[width=\twidth ]{eps/dcblockerfrlf}](http://www.dsprelated.com/josimages_new/filters/img1460.png) |
![\includegraphics[width=\twidth]{eps/dcblockerpz}](http://www.dsprelated.com/josimages_new/filters/img1461.png) |
Note that the amplitude response in Fig.B.11a and
Fig.B.12a exceeds 1 at half the sampling rate.
This maximum gain is given by
![]() . In applications for
which the gain must be bounded by 1 at all frequencies, the dc blocker
may be scaled by the inverse of this maximum gain to yield
. In applications for
which the gain must be bounded by 1 at all frequencies, the dc blocker
may be scaled by the inverse of this maximum gain to yield
![\begin{eqnarray*}
H(z) &=& g\frac{1-z^{-1}}{1-Rz^{-1}}\\
y(n) &=& g[x(n) - x(n-1)] + R\, y(n-1), \quad\hbox{where}\\
g &\isdef & \frac{1+R}{2}.
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/filters/img1464.png)
DC Blocker Software Implementations
In plain C, the difference equation for the dc blocker could be written as follows:
y = x - xm1 + 0.995 * ym1; xm1 = x; ym1 = y;Here, x denotes the current input sample, and y denotes the current output sample. The variables xm1 and ym1 hold once-delayed input and output samples, respectively (and are typically initialized to zero). In this implementation, the pole is fixed at
A complete C++ class implementing a dc blocking filter is included in the free, open-source Synthesis Tool Kit (STK) [15]. (See the DCBlock STK class.)
For a discussion of issues and solutions related to fixed-point implementations, see [7].
Next Section:
Low and High Shelving Filters
Previous Section:
Allpass Filter Sections








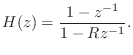
![\includegraphics[width=\twidth ]{eps/dcblockerir}](http://www.dsprelated.com/josimages_new/filters/img1462.png)











