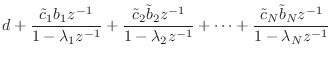Free Books
   Free Books    Introduction to Digital Filters  

Modal Representation

When the state transition matrix $ A$ is diagonal, we have the so-called modal representation. In the single-input, single-output (SISO) case, the general diagonal system looks like

$\displaystyle \left[\begin{array}{c} x_1(n+1) \\ [2pt] x_2(n+1) \\ [2pt] \vdots \\ [2pt] x_{N-1}(n+1)\\ [2pt] x_N(n+1)\end{array}\right]$ $\displaystyle =\!$ \begin{displaymath}\left[ \begin{array}{ccccc} \lambda _1 & 0 & 0 & \cdots & 0 \... ...ts \\ [2pt] b_{N-1}\\ [2pt] b_N\end{array}\right] u(n)\nonumber\end{displaymath}  
$\displaystyle y(n)$ $\displaystyle =$ $\displaystyle C {\underline{x}}(n) + du(n)$  
  $\displaystyle =$ $\displaystyle [c_1, c_2, \dots, c_N]{\underline{x}}(n) + d u(n). \protect$ (G.21)

Since the state transition matrix is diagonal, the modes are decoupled, and we can write each mode's time-update independently:

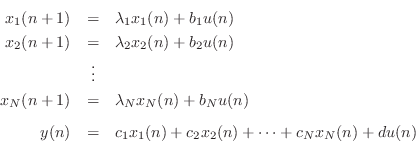
\begin{eqnarray*} x_1(n+1) &=& \lambda _1 x_1(n) + b_1 u(n)\\ x_2(n+1) &=& \lam... ...y(n) & = & c_1 x_1(n) + c_2 x_2(n) + \dots + c_N x_N(n) + d u(n) \end{eqnarray*}

Thus, the diagonalized state-space system consists of $ N$ parallel one-pole systems. See §9.2.2 and §6.8.7 regarding the conversion of direct-form filter transfer functions to parallel (complex) one-pole form.

Diagonalizing a State-Space Model

To obtain the modal representation, we may diagonalize any state-space representation. This is accomplished by means of a particular similarity transformation specified by the eigenvectors of the state transition matrix $ A$. An eigenvector of the square matrix $ A$ is any vector $ \underline{e}_i$ for which

$\displaystyle A\underline{e}_i= \lambda_i \underline{e}_i, $

where $ \lambda_i $ may be complex. In other words, when the matrix $ E$ of the similarity transformation is composed of the eigenvectors of $ A$,

$\displaystyle E= \left[ \underline{e}_1 \; \cdots \; \underline{e}_N \right], $

the transformed system will be diagonalized, as we will see below.

A system can be diagonalized whenever the eigenvectors of $ A$ are linearly independent. This always holds when the system poles are distinct. It may or may not hold when poles are repeated.

To see how this works, suppose we are able to find $ N$ linearly independent eigenvectors of $ A$, denoted $ \underline{e}_i$, $ i=1,\ldots,N$. Then we can form an $ N\times N$ matrix $ E$ having these eigenvectors as columns. Since the eigenvectors are linearly independent, $ E$ is full rank and can be used as a one-to-one linear transformation, or change-of-coordinates matrix. From Eq.$ \,$(G.19), we have that the transformed state transition matrix is given by

$\displaystyle \tilde{A}= E^{-1}A E $

Since each column $ \underline{e}_i$ of $ E$ is an eigenvector of $ A$, we have $ A\underline{e}_i=\lambda_i \underline{e}_i$, $ i=1,\ldots,N$, which implies

$\displaystyle A E= E\Lambda, $

where

$\displaystyle \Lambda \isdef \left[\begin{array}{ccc} \lambda_1 & & 0\\ [2pt] & \ddots & \\ [2pt] 0 & & \lambda_N \end{array}\right] $

is a diagonal matrix having the (complex) eigenvalues of $ A$ along the diagonal. It then follows that

$\displaystyle \tilde{A}= E^{-1}A E= E^{-1}E\Lambda = \Lambda, $

which shows that the new state transition matrix is diagonal and made up of the eigenvalues of $ A$.

The transfer function is now, from Eq.$ \,$(G.5), in the SISO case,

$\displaystyle H(z)$ $\displaystyle =$ $\displaystyle d + {\tilde C}\left(zI - \Lambda\right)^{-1}{\tilde B}$  
  $\displaystyle =$ $\displaystyle d + \frac{{\tilde c}_1 b_1 z^{-1}}{1 - \lambda _1z^{-1}} + \frac{... ...^{-1}} + \cdots + \frac{{\tilde c}_N {\tilde b}_N z^{-1}}{1 - \lambda _Nz^{-1}}$  
  $\displaystyle =$ $\displaystyle d + \sum_{i=1}^N \frac{{\tilde c}_i {\tilde b}_i z^{-1}}{1 - \lambda _iz^{-1}}. \protect$ (G.22)

We have incidentally shown that the eigenvalues of the state-transition matrix $ A$ are the poles of the system transfer function. When it is diagonal, i.e., when $ A =$   diag$ (\lambda _1,\ldots,\lambda _N)$, the state-space model may be called a modal representation of the system, because the poles appear explicitly along the diagonal of $ A$ and the system's dynamic modes are decoupled.

Notice that the diagonalized state-space form is essentially equivalent to a partial-fraction expansion form (§6.8). In particular, the residue of the $ i$th pole is given by $ c_i b_i$. When complex-conjugate poles are combined to form real, second-order blocks (in which case $ A$ is block-diagonal with $ 2\times 2$ blocks along the diagonal), this is corresponds to a partial-fraction expansion into real, second-order, parallel filter sections.

Finding the Eigenvalues of A in Practice

Small problems may be solved by hand by solving the system of equations

$\displaystyle A E= E\Lambda. $

The Matlab built-in function eig() may be used to find the eigenvalues of $ A$ (system poles) numerically.G.10

Example of State-Space Diagonalization

For the example of Eq.$ \,$(G.7), we obtain the following results: 

>> % Initial state space filter from example above:
>> A = [-1/2, -1/3; 1, 0]; % state transition matrix
>> B = [1; 0];
>> C = [2-1/2, 3-1/3];
>> D = 1;
>>
>> eig(A) % find eigenvalues of state transition matrix A

ans =
  -0.2500 + 0.5204i
  -0.2500 - 0.5204i

>> roots(den) % find poles of transfer function H(z)

ans =
  -0.2500 + 0.5204i
  -0.2500 - 0.5204i

>> abs(roots(den)) % check stability while we're here

ans =
    0.5774
    0.5774

% The system is stable since each pole has magnitude < 1.

Our second-order example is already in real $ 2\times 2$ form, because it is only second order. However, to illustrate the computations, let's obtain the eigenvectors and compute the complex modal representation: 

>> [E,L] = eig(A)  % [Evects,Evals] = eig(A)

E =

  -0.4507 - 0.2165i  -0.4507 + 0.2165i
        0 + 0.8660i        0 - 0.8660i


L =

  -0.2500 + 0.5204i        0
        0            -0.2500 - 0.5204i

>> A * E - E * L   % should be zero (A * evect = eval * evect)

ans =
  1.0e-016 *
        0 + 0.2776i        0 - 0.2776i
        0                  0

% Now form the complete diagonalized state-space model (complex):

>> Ei = inv(E); % matrix inverse
>> Ab = Ei*A*E % new state transition matrix (diagonal)

Ab =
  -0.2500 + 0.5204i   0.0000 + 0.0000i
  -0.0000            -0.2500 - 0.5204i

>> Bb = Ei*B   % vector routing input signal to internal modes

Bb =
   -1.1094
   -1.1094

>> Cb = C*E    % vector taking mode linear combination to output

Cb =
  -0.6760 + 1.9846i  -0.6760 - 1.9846i

>> Db = D      % feed-through term unchanged

Db =
     1

% Verify that we still have the same transfer function:

>> [numb,denb] = ss2tf(Ab,Bb,Cb,Db)

numb =
   1.0000             2.0000 + 0.0000i   3.0000 + 0.0000i

denb =
   1.0000             0.5000 - 0.0000i   0.3333

>> num = [1, 2, 3]; % original numerator
>> norm(num-numb)

ans =
  1.5543e-015

>> den = [1, 1/2, 1/3]; % original denominator
>> norm(den-denb)

ans =
  1.3597e-016

Properties of the Modal Representation

The vector $ {\tilde B}$ in a modal representation (Eq.$ \,$(G.21)) specifies how the modes are driven by the input. That is, the $ i$th mode receives the input signal $ u(n)$ weighted by $ {\tilde b}_i$. In a computational model of a drum, for example, $ {\tilde B}$ may be changed corresponding to different striking locations on the drumhead.

The vector $ {\tilde C}$ in a modal representation (Eq.$ \,$(G.21)) specifies how the modes are to be mixed into the output. In other words, $ {\tilde C}$ specifies how the output signal is to be created as a linear combination of the mode states:

$\displaystyle y(n) = {\tilde C}\underline{{\tilde x}}(n) = {\tilde c}_1 {\tilde x}_1(n) + {\tilde c}_2 {\tilde x}_2(n) + \cdots + {\tilde c}_N {\tilde x}_N(n) $

In a computational model of an electric guitar string, for example, $ {\tilde C}$ changes whenever a different pick-up is switched in or out (or is moved [99]).

The modal representation is not unique since $ {\tilde B}$ and $ {\tilde C}$ may be scaled in compensating ways to produce the same transfer function. (The diagonal elements of $ \tilde{A}$ may also be permuted along with $ {\tilde B}$ and $ {\tilde C}$.) Each element of the state vector $ \underline{{\tilde x}}(n)$ holds the state of a single first-order mode of the system.

For oscillatory systems, the diagonalized state transition matrix must contain complex elements. In particular, if mode $ i$ is both oscillatory and undamped (lossless), then an excited state-variable $ {\tilde x}_i(n)$ will oscillate sinusoidally, after the input becomes zero, at some frequency $ \omega_i$, where

$\displaystyle \lambda _i = e^{j\omega_iT} $

relates the system eigenvalue $ \lambda_i $ to the oscillation frequency $ \omega_i$, with $ T$ denoting the sampling interval in seconds. More generally, in the damped case, we have

$\displaystyle \lambda _i = R_i e^{j\omega_iT} $

where $ R_i$ is the pole (eigenvalue) radius. For stability, we must have

$\displaystyle \left\vert R_i\right\vert<1. $

In practice, we often prefer to combine complex-conjugate pole-pairs to form a real, ``block-diagonal'' system; in this case, the transition matrix $ \tilde{A}$ is block-diagonal with two-by-two real matrices along its diagonal of the form

$\displaystyle \mathbf{A}_i = \left[\begin{array}{cc} 2R_iC_i & -R_i^2 \\ [2pt] 1 & 0 \end{array}\right] $

where $ R_i=\left\vert\lambda_i\right\vert$ is the pole radius, and $ 2R_iC_i \isdef 2R_i\cos(\omega_i T) = \lambda_i + \overline{\lambda_i} = 2$re$ \left\{\lambda_i\right\}$. Note that, for real systems, a real second order block requires only two multiplies (one in the lossless case) per time update, while a complex second-order system requires two complex multiplies. The function cdf2rdf() in the Matlab Control Toolbox can be used to convert complex diagonal form to real block-diagonal form.

Next Section:
Repeated Poles
Previous Section:
Similarity Transformations