DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

State-Space Analysis Example:
The Digital Waveguide Oscillator

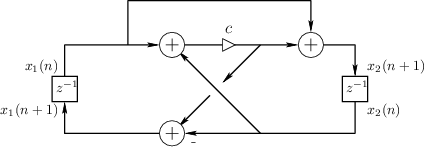
As an example of state-space analysis, we will use it to determine the frequency of oscillation of the system of Fig.G.3 [90].

Figure G.3: The second-order digital waveguide oscillator.
\begin{figure}\input fig/sswgo.pstex_t \end{figure}

Note the assignments of unit-delay outputs to state variables $ x_1(n)$ and $ x_2(n)$. From the diagram, we see that

$\displaystyle x_1(n+1) = c[x_1(n) + x_2(n)] - x_2(n) = c\,x_1(n) + (c-1) x_2(n) $

and

$\displaystyle x_2(n+1) = x_1(n) + c[x_1(n) + x_2(n)] = (1+c) x_1(n) + c\,x_2(n) $

In matrix form, the state time-update can be written

$\displaystyle \left[\begin{array}{c} x_1(n+1) \\ [2pt] x_2(n+1) \end{array}\rig... ...ay}\right]}_A \left[\begin{array}{c} x_1(n) \\ [2pt] x_2(n) \end{array}\right] $

or, in vector notation,

$\displaystyle {\underline{x}}(n+1) = A \, {\underline{x}}(n). $

We have two natural choices of output, $ x_1(n)$ and $ x_2(n)$:

\begin{eqnarray*} y_1(n) &\isdef & x_1(n) = [1, 0] {\underline{x}}(n)\\ y_2(n) &\isdef & x_2(n) = [0, 1] {\underline{x}}(n) \end{eqnarray*}

A basic fact from linear algebra is that the determinant of a matrix is equal to the product of its eigenvalues. As a quick check, we find that the determinant of $ A$ is

$\displaystyle \det{A} = c^2 - (c+1)(c-1) = c^2 - (c^2-1) = 1. $

Since an undriven sinusoidal oscillator must not lose energy, and since every lossless state-space system has unit-modulus eigenvalues (consider the modal representation), we expect $ \left\vert\det{A}\right\vert=1$.

Note that $ {\underline{x}}(n) = A^n{\underline{x}}(0)$. If we diagonalize this system to obtain $ \tilde{A}=E^{-1}A E$, where $ \tilde{A}=$   diag$ [\lambda_1,\lambda_2]$, and $ E$ is the matrix of eigenvectors of $ A$, then we have

$\displaystyle \underline{{\tilde x}}(n) = \tilde{A}^n\,\underline{{\tilde x}}(0... ...t[\begin{array}{c} {\tilde x}_1(0) \\ [2pt] {\tilde x}_2(0) \end{array}\right] $

where $ \underline{{\tilde x}}(n) \isdef E^{-1}{\underline{x}}(n)$ denotes the state vector in these new ``modal coordinates''. Since $ \tilde{A}$ is diagonal, the modes are decoupled, and we can write

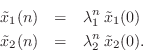
\begin{eqnarray*} {\tilde x}_1(n) &=& \lambda_1^n\,{\tilde x}_1(0)\\ {\tilde x}_2(n) &=& \lambda_2^n\,{\tilde x}_2(0). \end{eqnarray*}

If this system is to generate a real sampled sinusoid at radian frequency $ \omega$, the eigenvalues $ \lambda_1$ and $ \lambda_2$ must be of the form

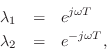
\begin{eqnarray*} \lambda_1 &=& e^{j\omega T}\\ \lambda_2 &=& e^{-j\omega T}, \end{eqnarray*}

(in either order) where $ \omega$ is real, and $ T$ denotes the sampling interval in seconds.

Thus, we can determine the frequency of oscillation $ \omega$ (and verify that the system actually oscillates) by determining the eigenvalues $ \lambda_i $ of $ A$. Note that, as a prerequisite, it will also be necessary to find two linearly independent eigenvectors of $ A$ (columns of $ E$).

Finding the Eigenstructure of A

Starting with the defining equation for an eigenvector $ \underline{e}$ and its corresponding eigenvalue $ \lambda$,

$\displaystyle A\underline{e}_i= \lambda_i \underline{e}_i,\quad i=1,2 $

we get

$\displaystyle \left[\begin{array}{cc} c & c-1 \\ [2pt] c+1 & c \end{array}\righ... ...egin{array}{c} \lambda_i \\ [2pt] \lambda_i \eta_i \end{array}\right]. \protect$ (G.23)

We normalized the first element of $ \underline{e}_i$ to 1 since $ g\underline{e}_i$ is an eigenvector whenever $ \underline{e}_i$ is. (If there is a missing solution because its first element happens to be zero, we can repeat the analysis normalizing the second element to 1 instead.)

Equation (G.23) gives us two equations in two unknowns:

$\displaystyle c+\eta_i (c-1)$ $\displaystyle =$ $\displaystyle \lambda_i \protect$ (G.24)
$\displaystyle (1+c) +c\eta_i$ $\displaystyle =$ $\displaystyle \lambda_i \eta_i$ (G.25)

Substituting the first into the second to eliminate $ \lambda_i $, we get

\begin{eqnarray*} 1+c+c\eta_i &=& [c+\eta_i (c-1)]\eta_i = c\eta_i + \eta_i ^2 (... ...-1)\\ \,\,\Rightarrow\,\,\eta_i &=& \pm \sqrt{\frac{c+1}{c-1}}. \end{eqnarray*}

Thus, we have found both eigenvectors

\begin{eqnarray*} \underline{e}_1&=&\left[\begin{array}{c} 1 \\ [2pt] \eta \end{... ...ght], \quad \hbox{where}\\ \eta&\isdef &\sqrt{\frac{c+1}{c-1}}. \end{eqnarray*}

They are linearly independent provided $ \eta\neq0\Leftrightarrow c\neq -1$ and finite provided $ c\neq 1$.

We can now use Eq.$ \,$(G.24) to find the eigenvalues:

$\displaystyle \lambda_i = c + \eta_i (c-1) = c \pm \sqrt{\frac{c+1}{c-1} (c-1)^2} = c \pm \sqrt{c^2-1} $

Assuming $ \left\vert c\right\vert<1$, the eigenvalues are

$\displaystyle \lambda_i = c \pm j\sqrt{1-c^2} \protect$ (G.26)

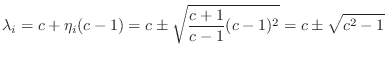
and so this is the range of $ c$ corresponding to sinusoidal oscillation. For $ \left\vert c\right\vert>1$, the eigenvalues are real, corresponding to exponential growth and decay. The values $ c=\pm 1$ yield a repeated root (dc or $ f_s/2$ oscillation).

Let us henceforth assume $ -1 < c < 1$. In this range $ \theta \isdef \arccos(c)$ is real, and we have $ c=\cos(\theta)$, $ \sqrt{1-c^2} = \sin(\theta)$. Thus, the eigenvalues can be expressed as follows:

\begin{eqnarray*} \lambda_1 &=& c + j\sqrt{1-c^2} = \cos(\theta) + j\sin(\theta)... ...- j\sqrt{1-c^2} = \cos(\theta) - j\sin(\theta) = e^{-j\theta}\\ \end{eqnarray*}

Equating $ \lambda_i $ to $ e^{j\omega_i T}$, we obtain $ \omega_i T = \pm \theta$, or $ \omega_i = \pm \theta/T = \pm f_s\theta = \pm f_s\arccos(c)$, where $ f_s$ denotes the sampling rate. Thus the relationship between the coefficient $ c$ in the digital waveguide oscillator and the frequency of sinusoidal oscillation $ \omega$ is expressed succinctly as

$\displaystyle \fbox{$\displaystyle c = \cos(\omega T).$} $

We see that the coefficient range (-1,1) corresponds to frequencies in the range $ (-f_s/2,f_s/2)$, and that's the complete set of available digital frequencies.

We have now shown that the system of Fig.G.3 oscillates sinusoidally at any desired digital frequency $ \omega$ rad/sec by simply setting $ c=\cos(\omega T)$, where $ T$ denotes the sampling interval.

Choice of Output Signal and Initial Conditions

Recalling that $ {\tilde x}= E\underline{{\tilde x}}$, the output signal from any diagonal state-space model is a linear combination of the modal signals. The two immediate outputs $ x_1(n)$ and $ x_2(n)$ in Fig.G.3 are given in terms of the modal signals $ {\tilde x}_1(n) = \lambda_1^n{\tilde x}_1(0)$ and $ {\tilde x}_2(n)= \lambda_2^n{\tilde x}_2(0)$ as

\begin{eqnarray*} y_1(n) &=& [1, 0] {\underline{x}}(n) = [1, 0] \left[\begin{arr... ...\lambda_1^n {\tilde x}_1(0) - \eta \lambda_2^n\,{\tilde x}_2(0). \end{eqnarray*}

The output signal from the first state variable $ x_1(n)$ is

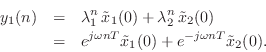
\begin{eqnarray*} y_1(n) &=& \lambda_1^n\,{\tilde x}_1(0) + \lambda_2^n\,{\tilde... ...{j\omega n T} {\tilde x}_1(0) + e^{-j\omega n T}{\tilde x}_2(0). \end{eqnarray*}

The initial condition $ {\underline{x}}(0) = [1, 0]^T$ corresponds to modal initial state

$\displaystyle \underline{{\tilde x}}(0) = E^{-1}\left[\begin{array}{c} 1 \\ [2p... ...nd{array}\right] = \left[\begin{array}{c} 1/2 \\ [2pt] 1/2 \end{array}\right]. $

For this initialization, the output $ y_1$ from the first state variable $ x_1$ is simply

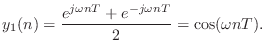
$\displaystyle y_1(n) = \frac{e^{j\omega n T} + e^{-j\omega n T}}{2} = \cos(\omega n T). $

A similar derivation can be carried out to show that the output $ y_2(n) = x_2(n)$ is proportional to $ \sin(\omega nT)$, i.e., it is in phase quadrature with respect to $ y_1(n)=x_1(n)$). Phase-quadrature outputs are often useful in practice, e.g., for generating complex sinusoids.

Next Section:
References
Previous Section:
Repeated Poles