Spectrum Analysis of a Sinusoid: Windowing, Zero-Padding, and FFT

Spectrum Analysis of a Sinusoid:
Windowing, Zero-Padding, and FFT

The examples below give a progression from the most simplistic analysis up to a proper practical treatment. Careful study of these examples will teach you a lot about how spectrum analysis is carried out on real data, and provide opportunities to see the Fourier theorems in action.

FFT of a Simple Sinusoid

Our first example is an FFT of the simple sinusoid

$\displaystyle x(n) = \cos(\omega_x n T)$

where we choose $\omega_x=2\pi(f_s/4)$ (frequency

Hz) and

(sampling rate

set to 1). Since we're using a Cooley-Tukey FFT, the signal length

should be a power of

for fastest results. Here is the Matlab code:

% Example 1: FFT of a DFT-sinusoid

% Parameters:
N = 64;              % Must be a power of two
T = 1;               % Set sampling rate to 1
A = 1;               % Sinusoidal amplitude
phi = 0;             % Sinusoidal phase
f = 0.25;            % Frequency (cycles/sample)
n = [0:N-1];         % Discrete time axis
x = A*cos(2*pi*n*f*T+phi); % Sampled sinusoid
X = fft(x);          % Spectrum

% Plot time data:
figure(1);
subplot(3,1,1);
plot(n,x,'*k');
ni = [0:.1:N-1];     % Interpolated time axis
hold on;
plot(ni,A*cos(2*pi*ni*f*T+phi),'-k'); grid off;
title('Sinusoid at 1/4 the Sampling Rate');
xlabel('Time (samples)');
ylabel('Amplitude');
text(-8,1,'a)');
hold off;

% Plot spectral magnitude:
magX = abs(X);
fn = [0:1/N:1-1/N];  % Normalized frequency axis
subplot(3,1,2);
stem(fn,magX,'ok'); grid on;
xlabel('Normalized Frequency (cycles per sample))');
ylabel('Magnitude (Linear)');
text(-.11,40,'b)');

% Same thing on a dB scale:
spec = 20*log10(magX); % Spectral magnitude in dB
subplot(3,1,3);
plot(fn,spec,'--ok'); grid on;
axis([0 1 -350 50]);
xlabel('Normalized Frequency (cycles per sample))');
ylabel('Magnitude (dB)');
text(-.11,50,'c)');
cmd = ['print -deps ', '../eps/example1.eps'];
disp(cmd); eval(cmd);

**Figure 8.1:** Sampled sinusoid at frequency . a) Time waveform. b) Magnitude spectrum. c) DB magnitude spectrum.
$\includegraphics[width=\twidth]{eps/example1}$

The results are shown in Fig.8.1. The time-domain signal is shown in the upper plot (Fig.8.1a), both in pseudo-continuous and sampled form. In the middle plot (Fig.8.1b), we see two peaks in the magnitude spectrum, each at magnitude on a linear scale, located at normalized frequencies and . A spectral peak amplitude of is what we expect, since

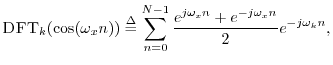
$\displaystyle \hbox{\sc DFT}_k(\cos(\omega_x n)) \isdef \sum_{n=0}^{N-1} \frac{e^{j\omega_x n} + e^{-j\omega_x n}}{2} e^{-j\omega_k n},$

and when $\omega_k=\pm\omega_x$ , this reduces to

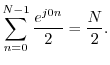
$\displaystyle \sum_{n=0}^{N-1}\frac{e^{j 0 n}}{2} = \frac{N}{2}.$

For

and $\omega_x=2\pi f_s/4$ , this happens at bin numbers

and

. However, recall that array indexes in matlab start at

, so that these peaks will really show up at indexes

and

in the magX array.

The spectrum should be exactly zero at the other bin numbers. How accurately this happens can be seen by looking on a dB scale, as shown in Fig.8.1c. We see that the spectral magnitude in the other bins is on the order of dB lower, which is close enough to zero for audio work $(\stackrel{\mbox{.\,.}}{\smile})$ .

FFT of a Not-So-Simple Sinusoid

Now let's increase the frequency in the above example by one-half of a bin:

% Example 2 = Example 1 with frequency between bins

f = 0.25 + 0.5/N;   % Move frequency up 1/2 bin

x = cos(2*pi*n*f*T); % Signal to analyze
X = fft(x);          % Spectrum
...                  % See Example 1 for plots and such

**Figure 8.2:** Sinusoid at Frequency . a) Time waveform. b) Magnitude spectrum. c) DB magnitude spectrum.
$\includegraphics[width=\twidth]{eps/example2}$

The resulting magnitude spectrum is shown in Fig.8.2b and c. At this frequency, we get extensive ``spectral leakage'' into all the bins. To get an idea of where this is coming from, let's look at the periodic extension (§7.1.2) of the time waveform:

% Plot the periodic extension of the time-domain signal
plot([x,x],'--ok');
title('Time Waveform Repeated Once');
xlabel('Time (samples)'); ylabel('Amplitude');

The result is shown in Fig.8.3. Note the ``glitch'' in the middle where the signal begins its forced repetition.

**Figure 8.3:** Time waveform repeated to show discontinuity introduced by periodic extension (see midpoint).
$\includegraphics[width=\twidth,height=2in]{eps/waveform2}$

FFT of a Zero-Padded Sinusoid

Looking back at Fig.8.2c, we see there are no negative dB values. Could this be right? Could the spectral magnitude at all frequencies be 1 or greater? The answer is no. To better see the true spectrum, let's use zero padding in the time domain (§7.2.7) to give ideal interpolation (§7.4.12) in the frequency domain:

zpf = 8;            % zero-padding factor
x = [cos(2*pi*n*f*T),zeros(1,(zpf-1)*N)]; % zero-padded
X = fft(x);         % interpolated spectrum
magX = abs(X);      % magnitude spectrum
...                 % waveform plot as before
nfft = zpf*N;       % FFT size = new frequency grid size
fni = [0:1.0/nfft:1-1.0/nfft]; % normalized freq axis
subplot(3,1,2);
% with interpolation, we can use solid lines '-':
plot(fni,magX,'-k'); grid on;
...
spec = 20*log10(magX); % spectral magnitude in dB
% clip below at -40 dB:
spec = max(spec,-40*ones(1,length(spec)));
...                 % plot as before

**Figure 8.4:** Zero-padded sinusoid at frequency cycles/sample. a) Time waveform. b) Magnitude spectrum. c) DB magnitude spectrum.
$\includegraphics[width=\twidth]{eps/example3}$

Figure 8.4 shows the zero-padded data (top) and corresponding interpolated spectrum on linear and dB scales (middle and bottom, respectively). We now see that the spectrum has a regular sidelobe structure. On the dB scale in Fig.8.4c, negative values are now visible. In fact, it was desirable to clip them at dB to prevent deep nulls from dominating the display by pushing the negative vertical axis limit to dB or more, as in Fig.8.1c (page ). This example shows the importance of using zero padding to interpolate spectral displays so that the untrained eye will ``fill in'' properly between the spectral samples.

Use of a Blackman Window

As Fig.8.4a suggests, the previous example can be interpreted as using a rectangular window to select a finite segment (of length ) from a sampled sinusoid that continues for all time. In practical spectrum analysis, such excerpts are normally analyzed using a window that is tapered more gracefully to zero on the left and right. In this section, we will look at using a Blackman window [70]^8.3on our example sinusoid. The Blackman window has good (though suboptimal) characteristics for audio work.

In Octave^8.4or the Matlab Signal Processing Toolbox,^8.5a Blackman window of length can be designed very easily:

M = 64;
w = blackman(M);

Many other standard windows are defined as well, including hamming, hanning, and bartlett windows.

In Matlab without the Signal Processing Toolbox, the Blackman window is readily computed from its mathematical definition:

w = .42 - .5*cos(2*pi*(0:M-1)/(M-1)) ...
       + .08*cos(4*pi*(0:M-1)/(M-1));

Figure 8.5 shows the Blackman window and its magnitude spectrum on a dB scale. Fig.8.5c uses the more ``physical'' frequency axis in which the upper half of the FFT bin numbers are interpreted as negative frequencies. Here is the complete Matlab script for Fig.8.5:

M = 64;
w = blackman(M);
figure(1);
subplot(3,1,1); plot(w,'*'); title('Blackman Window');
xlabel('Time (samples)'); ylabel('Amplitude'); text(-8,1,'a)');

% Also show the window transform:
zpf = 8;                      % zero-padding factor
xw = [w',zeros(1,(zpf-1)*M)]; % zero-padded window
Xw = fft(xw);                 % Blackman window transform
spec = 20*log10(abs(Xw));     % Spectral magnitude in dB
spec = spec - max(spec);      % Normalize to 0 db max
nfft = zpf*M;
spec = max(spec,-100*ones(1,nfft)); % clip to -100 dB
fni = [0:1.0/nfft:1-1.0/nfft];   % Normalized frequency axis
subplot(3,1,2); plot(fni,spec,'-'); axis([0,1,-100,10]);
xlabel('Normalized Frequency (cycles per sample))');
ylabel('Magnitude (dB)'); grid; text(-.12,20,'b)');

% Replot interpreting upper bin numbers as frequencies<0:
nh = nfft/2;
specnf = [spec(nh+1:nfft),spec(1:nh)];  % see fftshift()
fninf = fni - 0.5;
subplot(3,1,3);
plot(fninf,specnf,'-'); axis([-0.5,0.5,-100,10]); grid;
xlabel('Normalized Frequency (cycles per sample))');
ylabel('Magnitude (dB)');
text(-.62,20,'c)');
cmd = ['print -deps ', '../eps/blackman.eps'];
disp(cmd); eval(cmd);
disp 'pausing for RETURN (check the plot). . .'; pause

**Figure 8.5:** The Blackman window: a) window itself in the time domain, b) dB magnitude spectrum plotted over normalized frequencies , and c) same thing plotted over .
$\includegraphics[width=\twidth]{eps/blackman}$

Applying the Blackman Window

Now let's apply the Blackman window to the sampled sinusoid and look at the effect on the spectrum analysis:

% Windowed, zero-padded data:
n = [0:M-1];          % discrete time axis
f = 0.25 + 0.5/M;     % frequency
xw = [w .* cos(2*pi*n*f),zeros(1,(zpf-1)*M)];

% Smoothed, interpolated spectrum:
X = fft(xw);

% Plot time data:
subplot(2,1,1);
plot(xw);
title('Windowed, Zero-Padded, Sampled Sinusoid');
xlabel('Time (samples)');
ylabel('Amplitude');
text(-50,1,'a)');

% Plot spectral magnitude:
spec = 10*log10(conj(X).*X);  % Spectral magnitude in dB
spec = max(spec,-60*ones(1,nfft)); % clip to -60 dB
subplot(2,1,2);
plot(fninf,fftshift(spec),'-');
axis([-0.5,0.5,-60,40]);
title('Smoothed, Interpolated, Spectral Magnitude (dB)');
xlabel('Normalized Frequency (cycles per sample))');
ylabel('Magnitude (dB)'); grid;
text(-.6,40,'b)');

Figure 8.6 plots the zero-padded, Blackman-windowed sinusoid, along with its magnitude spectrum on a dB scale. Note that the first sidelobe (near

dB) is nearly 60 dB below the spectral peak (near

dB). This is why the Blackman window is considered adequate for many audio applications. From the dual of the convolution theorem discussed in §7.4.6, we know that windowing in the time domain corresponds to smoothing in the frequency domain. Specifically, the complex spectrum with magnitude displayed in Fig.8.4b (p.

) has been convolved with the Blackman window transform (dB magnitude shown in Fig.8.5c). Thus, the Blackman window Fourier transform has been applied as a smoothing kernel to the Fourier transform of the rectangularly windowed sinusoid to produce the smoothed result in Fig.8.6b. This topic is pursued in detail at the outset of Book IV in the music signal processing series [70].

**Figure 8.6:** Effect of the Blackman window on the sinusoidal data.
$\includegraphics[width=\twidth]{eps/xw}$

Hann-Windowed Complex Sinusoid

In this example, we'll perform spectrum analysis on a complex sinusoid having only a single positive frequency. We'll use the Hann window (also known as the Hanning window) which does not have as much sidelobe suppression as the Blackman window, but its main lobe is narrower. Its sidelobes ``roll off'' very quickly versus frequency. Compare with the Blackman window results to see if you can see these differences.

The Matlab script for synthesizing and plotting the Hann-windowed sinusoid is given below:

% Analysis parameters:
M = 31;         % Window length
N = 64;         % FFT length (zero padding factor near 2)

% Signal parameters:
wxT = 2*pi/4;   % Sinusoid frequency (rad/sample)
A = 1;          % Sinusoid amplitude
phix = 0;       % Sinusoid phase

% Compute the signal x:
n = [0:N-1];    % time indices for sinusoid and FFT
x = A * exp(j*wxT*n+phix); % complex sine [1,j,-1,-j...]

% Compute Hann window:
nm = [0:M-1];   % time indices for window computation
% Hann window = "raised cosine", normalization (1/M)
% chosen to give spectral peak magnitude at 1/2:
w = (1/M) * (cos((pi/M)*(nm-(M-1)/2))).^2;

wzp = [w,zeros(1,N-M)]; % zero-pad out to the length of x
xw = x .* wzp;          % apply the window w to signal x

figure(1);
subplot(1,1,1);

% Display real part of windowed signal and Hann window
plot(n,wzp,'-k'); hold on; plot(n,real(xw),'*k'); hold off;
title(['Hann Window and Windowed, Zero-Padded, ',...
       'Sinusoid (Real Part)']);
xlabel('Time (samples)'); ylabel('Amplitude');

The resulting plot of the Hann window and its use on sinusoidal data are shown in Fig.8.7.

**Figure 8.7:** A length 31 Hann window (``raised cosine'') overlaid with the real part of the Hann-windowed complex sinusoid. Zero-padding is also shown. The sampled sinusoid is plotted using `*' with no connecting interpolation lines. You must now imagine the continuous real sinusoid (windowed) threading through the asterisks.
$\includegraphics[width=\twidth]{eps/hanning}$

Hann Window Spectrum Analysis Results

Finally, the Matlab for computing the DFT of the Hann-windowed complex sinusoid and plotting the results is listed below. To help see the full spectrum, we also compute a heavily interpolated spectrum (via zero padding as before) which we'll draw using solid lines.

% Compute the spectrum and its alternative forms:
Xw = fft(xw);              % FFT of windowed data
fn = [0:1.0/N:1-1.0/N];    % Normalized frequency axis
spec = 20*log10(abs(Xw));  % Spectral magnitude in dB
% Since the nulls can go to minus infinity, clip at -100 dB:
spec = max(spec,-100*ones(1,length(spec)));
phs = angle(Xw);           % Spectral phase in radians
phsu = unwrap(phs);        % Unwrapped spectral phase

% Compute heavily interpolated versions for comparison:
Nzp = 16;                   % Zero-padding factor
Nfft = N*Nzp;               % Increased FFT size
xwi = [xw,zeros(1,Nfft-N)]; % New zero-padded FFT buffer
Xwi = fft(xwi);             % Compute interpolated spectrum
fni = [0:1.0/Nfft:1.0-1.0/Nfft]; % Normalized freq axis
speci = 20*log10(abs(Xwi)); % Interpolated spec mag (dB)
speci = max(speci,-100*ones(1,length(speci))); % clip
phsi = angle(Xwi);          % Interpolated phase
phsiu = unwrap(phsi);       % Unwrapped interpolated phase

figure(1);
subplot(2,1,1);

plot(fn,abs(Xw),'*k'); hold on;
plot(fni,abs(Xwi),'-k'); hold off;
title('Spectral Magnitude');
xlabel('Normalized Frequency (cycles per sample))');
ylabel('Amplitude (linear)');

subplot(2,1,2);

% Same thing on a dB scale
plot(fn,spec,'*k'); hold on; plot(fni,speci,'-k'); hold off;
title('Spectral Magnitude (dB)');
xlabel('Normalized Frequency (cycles per sample))');
ylabel('Magnitude (dB)');

cmd = ['print -deps ', 'specmag.eps']; disp(cmd); eval(cmd);
disp 'pausing for RETURN (check the plot). . .'; pause

figure(1);
subplot(2,1,1);
plot(fn,phs,'*k'); hold on; plot(fni,phsi,'-k'); hold off;
title('Spectral Phase');
xlabel('Normalized Frequency (cycles per sample))');
ylabel('Phase (rad)'); grid;
subplot(2,1,2);
plot(fn,phsu,'*k'); hold on; plot(fni,phsiu,'-k'); hold off;
title('Unwrapped Spectral Phase');
xlabel('Normalized Frequency (cycles per sample))');
ylabel('Phase (rad)'); grid;
cmd = ['print -deps ', 'specphs.eps']; disp(cmd); eval(cmd);

Figure 8.8 shows the spectral magnitude and Fig.8.9 the spectral phase.

**Figure 8.8:** Spectral magnitude on linear (top) and dB (bottom) scales.
$\includegraphics[width=\twidth]{eps/specmag}$

There are no negative-frequency components in Fig.8.8 because we are analyzing a complex sinusoid $x=[1,j,-1,-j,1,j,\ldots\,]$ , which has frequency only, with no component at .

Notice how difficult it would be to correctly interpret the shape of the ``sidelobes'' without zero padding. The asterisks correspond to a zero-padding factor of 2, already twice as much as needed to preserve all spectral information faithfully, but not enough to clearly outline the sidelobes in a spectral magnitude plot.

Spectral Phase

As for the phase of the spectrum, what do we expect? We have chosen the sinusoid phase offset to be zero. The window is causal and symmetric about its middle. Therefore, we expect a linear phase term with slope samples (as discussed in connection with the shift theorem in §7.4.4). Also, the window transform has sidelobes which cause a phase of $\pi$ radians to switch in and out. Thus, we expect to see samples of a straight line (with slope samples) across the main lobe of the window transform, together with a switching offset by $\pi$ in every other sidelobe away from the main lobe, starting with the immediately adjacent sidelobes.

In Fig.8.9(a), we can see the negatively sloped line across the main lobe of the window transform, but the sidelobes are hard to follow. Even the unwrapped phase in Fig.8.9(b) is not as clear as it could be. This is because a phase jump of $\pi$ radians and $-\pi$ radians are equally valid, as is any odd multiple of $\pi$ radians. In the case of the unwrapped phase, all phase jumps are by $+\pi$ starting near frequency . Figure 8.9(c) shows what could be considered the ``canonical'' unwrapped phase for this example: We see a linear phase segment across the main lobe as before, and outside the main lobe, we have a continuation of that linear phase across all of the positive sidelobes, and only a $\pi$ -radian deviation from that linear phase across the negative sidelobes. In other words, we see a straight linear phase at the desired slope interrupted by temporary jumps of $\pi$ radians. To obtain unwrapped phase of this type, the unwrap function needs to alternate the sign of successive phase-jumps by $\pi$ radians; this could be implemented, for example, by detecting jumps-by- $\pi$ to within some numerical tolerance and using a bit of state to enforce alternation of $+\pi$ with $-\pi$ .

To convert the expected phase slope from ``radians per (rad/sec)'' to ``radians per cycle-per-sample,'' we need to multiply by ``radians per cycle,'' or $2\pi$ . Thus, in Fig.8.9(c), we expect a slope of radians per unit normalized frequency, or radians per cycles-per-sample, and this looks about right, judging from the plot.

**Figure 8.9:** Spectral phase and two different phase unwrappings.
$\includegraphics{eps/% specphs-wrapped}$ Raw spectral phase and its interpolation 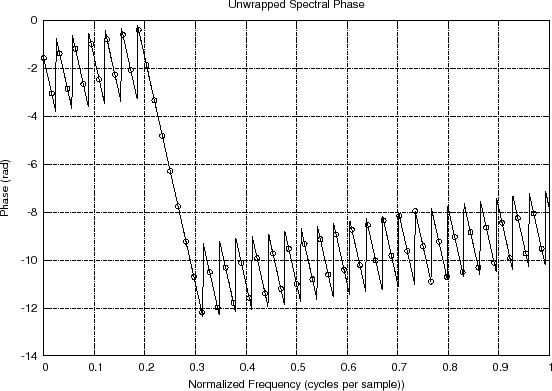$\includegraphics{eps/% specphs-unwrapped}$ Unwrapped spectral phase and its interpolation 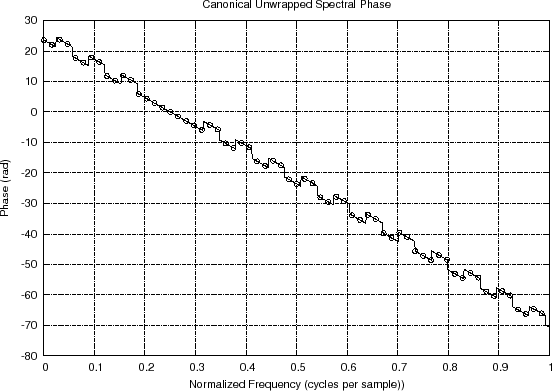$\includegraphics{eps/% specphs-unwrapped-linear}$ Canonically unwrapped spectral phase and its interpolation

Next Section:
Spectrograms
Previous Section:
DFT Theorems Problems