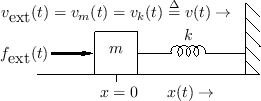DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Equivalent Circuits

The concepts of ``circuits'' and ``ports'' from classical circuit/network theory [35] are very useful for partitioning complex systems into self-contained sections having well-defined (small) interfaces. For example, it is typical in analog electric circuit design to drive a high-input-impedance stage from a low-output-impedance stage (a so-called ``voltage transfer'' connection). This large impedance ratio allows us to neglect ``loading effects'' so that the circuit sections (stages) can be analyzed separately.

The name ``analog circuit'' refers to the fact that electrical capacitors (denoted $ C$) are analogous to physical springs, inductors ($ L$) are analogous to physical masses, and resistors ($ R$) are analogous to ``dashpots'' (which are idealized physical devices for which compression velocity is proportional to applied force--much like a shock-absorber (``damper'') in an automobile suspension). These are all called lumped elements to distinguish them from distributed parameters such as the capacitance and inductance per unit length in an electrical transmission line. Lumped elements are described by ODEs while distributed-parameter systems are described by PDEs. Thus, RLC analog circuits can be constructed as equivalent circuits for lumped dashpot-mass-spring systems. These equivalent circuits can then be digitized by finite difference or wave digital methods. PDEs describing distributed-parameter systems can be digitized via finite difference methods as well, or, when wave propagation is the dominant effect, digital waveguide methods.

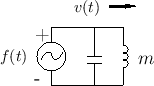
As discussed in Chapter 7 (§7.2), the equivalent circuit for a force-driven mass is shown in Fig.F.10. The mass $ m$ is represented by an inductor $ L=m$. The driving force $ f(t)$ is supplied via a voltage source, and the mass velocity $ v(t)$ is the loop current.

Figure: Electrical equivalent circuit of the force-driven mass in Fig.1.6.
\includegraphics{eps/forcemassecCopy}

As also discussed in Chapter 7 (§7.2), if two physical elements are connected in such a way that they share a common velocity, then they are said to be formally connected in series. The ``series'' nature of the connection becomes more clear when the equivalent circuit is considered.

Figure 1.9: A mass and spring connected in series.
\includegraphics{eps/lseriesExampleCopy}

For example, Fig.1.9 shows a mass connected to one end of a spring, with the other end of the spring attached to a rigid wall. The driving force $ f_{\mbox{ext}}(t)$ is applied to the mass $ m$ on the left so that a positive force results in a positive mass displacement $ x_m(t)$ and positive spring displacement (compression) $ x_k(t)$. Since the mass and spring displacements are physically the same, we can define $ x_m=x_k\isdeftext x$. Their velocities are similarly equal so that $ v_m=v_k\isdeftext v$. The equivalent circuit has their electrical analogs connected in series, as shown in Fig.1.10. The common mass and spring velocity $ v(t)$ appear as a single current running through the inductor (mass) and capacitor (spring).

Figure: Electrical equivalent circuit of the series mass-spring driven by an external force diagrammed in Fig.1.9.
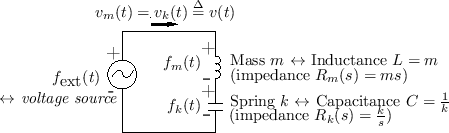\includegraphics{eps/lseriesecCopy}

By Kirchoff's loop law for circuit analysis, the sum of all voltages around a loop equals zero.2.13 Thus, following the direction for current $ v$ in Fig.1.10, we have $ f_m+f_k-f_{\mbox{ext}}=0$ (where the minus sign for $ f_{\mbox{ext}}=0$ occurs because the current enters its minus sign), or

$\displaystyle f_{\mbox{ext}}(t) \eqsp f_m(t)+f_k(t). $

Thus, the equivalent circuit agrees with our direct physical analysis that the applied force $ f_{\mbox{ext}}(t)$ is equal at all times to the sum of the mass inertial force $ f_m(t) = m\ddot{x}(t)$ and spring force $ f_k(t) = k x(t)$, i.e.,

$\displaystyle f_{\mbox{ext}}(t) \eqsp m\ddot{x}(t) + k x(t). $

Next Section:
Impedance Networks
Previous Section:
Modal Representation