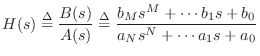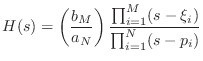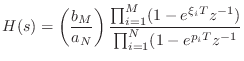Free Books
   Free Books    Physical Audio Signal Processing  

Matched Z Transformation

The matched z transformation uses the same pole-mapping Eq.$ \,$(8.2) as in the impulse-invariant method, but the zeros are handled differently. Instead of only mapping the poles of the partial fraction expansion and letting the zeros fall where they may, the matched z transformation maps both the poles and zeros in the factored form of the transfer function [362, pp. 224-226].

The factored form [449] of a transfer function

$\displaystyle H(s) \isdef \frac{B(s)}{A(s)} \isdef \frac{b_M s^M + \cdots b_1 s + b_0}{a_N s^N + \cdots a_1 s + a_0} \protect$ (9.3)

can be written as

$\displaystyle H(s) = \left(\frac{b_M}{a_N}\right) \frac{\prod_{i=1}^M (s-\xi_i) }{\prod_{i=1}^N (s-p_i) } \protect$ (9.4)

The matched z transformation is carried out by replacing each first-order term of the form $ (s+a)$ by its digital equivalent $ 1 - e^{-aT}z^{-1}$, i.e.,

$\displaystyle \zbox {s+a \;\to\; 1 - e^{-aT}z^{-1}} \protect$ (9.5)

to get

$\displaystyle H(s) = \left(\frac{b_M}{a_N}\right) \frac{ \prod_{i=1}^M (1 - e^{\xi_iT}z^{-1})}{ \prod_{i=1}^N (1 - e^{p_iT}z^{-1}} \protect$ (9.6)

Thus, the matched z transformation normally yields different digital zeros than the impulse-invariant method. The impulse-invariant method is generally considered superior to the matched z transformation [343].

Relation to Finite Difference Approximation

The Finite Difference Approximation (FDA) (§7.3.1) is a special case of the matched $ z$ transformation applied to the point $ s=0$. To see this, simply set $ a=0$ in Eq.$ \,$(8.5) to obtain

$\displaystyle s \;\to\; 1 - z^{-1} \protect$ (9.7)

which is the FDA definition in the frequency domain given in Eq.$ \,$(7.3).

Since the FDA equals the match z transformation for the point $ s=0$, it maps analog dc ($ s=0$) to digital dc ($ z=1$) exactly. However, that is the only point on the frequency axis that is perfectly mapped, as shown in Fig.7.15.

Next Section:
Pole Mapping with Optimal Zeros
Previous Section:
Impulse Invariant Method