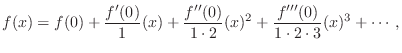DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Nonlinear Elements

Many musical instrument models require nonlinear elements, such as

Since a nonlinear element generally expands signal bandwidth, it can cause aliasing in a discrete-time implementation. In the above examples, the nonlinearity also appears inside a feedback loop. This means the bandwidth expansion compounds over time, causing more and more aliasing.

The topic of nonlinear systems analysis is vast, in part because there is no single analytical approach which is comprehensive. The situation is somewhat analogous to an attempt to characterize ``all non-bacterial life''. As a result, the only practical approach is to identify useful classes of nonlinear systems which are amenable to certain kinds of analysis and characterization. In this chapter, we will look at certain classes of memoryless and passive nonlinear elements which are often used in digital waveguide modeling.

It is important to keep in mind that a nonlinear element may not be characterized by its impulse response, frequency response, transfer function, or the like. These concepts are only defined, in general, for linear time-invariant systems. However, it is possible to generalize these notions for nonlinear systems using constructs such as Volterra series expansions [52]. However, rather than getting involved with fairly general analysis tools, we will focus instead on approaching each class of nonlinear elements in the manner that best fits that class, with the main goal being to understand its audible effects on discrete-time signals.

Memoryless Nonlinearities

Memoryless or instantaneous nonlinearities form the simplest and most commonly implemented form of nonlinear element. Furthermore, many complex nonlinear systems can be broken down into a linear system containing a memoryless nonlinearity.

Given a sampled input signal $ x(n)$, the output of any memoryless nonlinearity can be written as

$\displaystyle y(n) = f(x(n)) $

where $ f(\cdot)$ is ``some function'' which maps numbers to real numbers. We exclude the special case $ f(x)=\alpha x$ which defines a simple linear gain of $ \alpha$.

The fact that a function may be used to describe the nonlinearity implies that each input value is mapped to a unique output value. If it is also true that each output value is mapped to a unique input value, then the function is said to be one-to-one, and the mapping is invertible. If the function is instead ``many-to-one,'' then the inverse is ambiguous, with more than one input value corresponding to the same output value.

Clipping Nonlinearity

A simple example of a noninvertible (many-to-one) memoryless nonlinearity is the clipping nonlinearity, well known to anyone who records or synthesizes audio signals. In normalized form, the clipping nonlinearity is defined by

$\displaystyle f(x) = \left\{\begin{array}{ll} -1, & x\leq -1 \\ [5pt] x, & -1 \leq x \leq 1 \\ [5pt] 1, & x\geq 1 \\ \end{array} \right. \protect$ (7.17)

Since the clipping nonlinearity abruptly transitions from linear to hard-clipped in a non-invertible, heavily aliasing manner, it is usually desirable to use some form of soft-clipping before entering the hard-clipping range.

Arctangent Nonlinearity

A simple example of an invertible (one-to-one) memoryless nonlinearity is the arctangent mapping:

$\displaystyle f(x) = \frac{2}{\pi}\arctan(\alpha x), \quad x\in[-1,1] $

where normally $ \alpha\gg 1$. This function is graphed for $ \alpha=10$ in Fig.6.21. (Recall that $ \arctan(x)$ is defined as the angle whose tangent is $ x$. Only angles between $ -\pi /2$ and $ \pi /2$ are needed to cover all real values of $ x$.)

Figure 6.21: Arctangent nonlinearity.
\includegraphics[width=3in]{eps/atanex}

Cubic Soft Clipper

In §9.1.6, we used the cubic soft-clipper to simulate amplifier distortion:

$\displaystyle f(x) = \left\{\begin{array}{ll} -\frac{2}{3}, & x\leq -1 \\ [5pt]... ...{3}, & -1 \leq x \leq 1 \\ [5pt] \frac{2}{3}, & x\geq 1 \\ \end{array}\right. $

This function is diagrammed in Fig.6.22. It is non-invertible when driven into ``hard clipping''.

Figure 6.22: Cubic nonlinearity.
\includegraphics[width=3in]{eps/cnlCopy}

Series Expansions

Any ``smooth'' function $ f(x)$ can be expanded as a Taylor series expansion:

$\displaystyle f(x) = f(0) + \frac{f^\prime(0)}{1}(x) + \frac{f^{\prime\prime}(0... ...cdot 2}(x)^2 + \frac{f^{\prime\prime\prime}(0)}{1\cdot 2\cdot 3}(x)^3 + \cdots,$ (7.18)

where ``smooth'' means that derivatives of all orders must exist over the range of validity. Derivatives of all orders are obviously needed at $ x=0$ by the above expansion, and for the expansion to be valid everywhere, the function $ f(x)$ must be smooth for all $ x$.

Arctangent Series Expansion

For example, the arctangent function used above can be expanded as

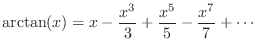
$\displaystyle \arctan(x) = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots $

Note that all even-order terms are zero. This is always the case for odd functions, i.e., functions satisfying $ f(-x)=-f(x)$. For any smooth function, the odd-order terms of its Taylor expansion comprise the odd part of the function, while the even-order terms comprise the even part. The original function is clearly given by the sum of its odd and even parts.7.17

The clipping nonlinearity in Eq.$ \,$(6.17) is not so amenable to a series expansion. In fact, it is its own series expansion! Since it is not differentiable at $ x=\pm1$, it must be represented as three separate series over the intervals $ (-\infty,1]$, $ [-1,1]$, and $ [1,\infty)$, and the result obtained over these intervals is precisely the definition of $ f(x)$ in Eq.$ \,$(6.17).

Spectrum of a Memoryless Nonlinearities

The series expansion of a memoryless nonlinearity is a useful tool for quantifying the aliasing caused by that nonlinear mapping when introduced into the signal path of a discrete-time system.

Square Law Series Expansion

When viewed as a Taylor series expansion such as Eq.$ \,$(6.18), the simplest nonlinearity is clearly the square law nonlinearity:

$\displaystyle f(x) = x + \alpha x^2 $

where $ \alpha$ is a parameter of the mapping.7.18

Consider a simple signal processing system consisting only of the square-law nonlinearity:

$\displaystyle y(n) = x(n) + \alpha x^2(n) $

The Fourier transform of the output signal is easily found using the dual of the convolution theorem:7.19

$\displaystyle Y(\omega) = X(\omega) + \alpha (X\ast X)(\omega) $

where ``$ \ast $'' denotes convolution. In general, the bandwidth of $ X\ast X$ is double that of $ X$.

Power Law Spectrum

More generally,

$\displaystyle x^k(n) \;\longleftrightarrow\; \underbrace{(X\ast X \ast \cdots \ast X)}_{\mbox{$k$\ times}}(\omega) $

so that the spectral bandwidth of $ x^k(n)$ is $ k$ times that of $ x(n)$, in general.

In summary, the spectrum at the output of the square-law nonlinearity can be written as

$\displaystyle Y(\omega) = X(\omega) + \alpha (X\ast X)(\omega) $

This illustrates the great value of series expansions for nonlinearities. In audio signal processing systems, it is essential to keep track of the spectral representation of all output signals, since we hear directly in terms of signal spectra.7.20

Arctangent Spectrum

Since the series expansion of the arctangent nonlinearity is

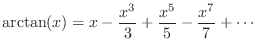
$\displaystyle \arctan(x) = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots $

bandwidth expansion is infinite (in continuous time). Thus, we expect problems with aliasing.

Cubic Soft-Clipper Spectrum

The cubic soft-clipper, like any polynomial nonlinearity, is defined directly by its series expansion:

$\displaystyle f(x) = \left\{\begin{array}{ll} -\frac{2}{3}, & x\leq -1 \\ [5pt]... ...{3}, & -1 \leq x \leq 1 \\ [5pt] \frac{2}{3}, & x\geq 1 \\ \end{array}\right. $ (7.19)

In the absence of hard-clipping ( $ \left\vert x\right\vert\leq1$), bandwidth expansion is limited to a factor of three. This is the slowest aliasing rate obtainable for an odd nonlinearity. Note that smoothing the ``corner'' in the clipping nonlinearity can reduce the severe bandwidth expansion associated with hard-clipping.

Stability of Nonlinear Feedback Loops

In general, placing a memoryless nonlinearity $ f(x)$ in a stable feedback loop preserves stability provided the gain of the nonlinearity is less than one, i.e., $ \vert f(x)\vert\le \vert x\vert$. A simple proof for the case of a loop consisting of a continuous-time delay-line and memoryless-nonlinearity is as follows.

The delay line can be interpreted as a waveguide model of an ideal string or acoustic pipe having wave impedance $ R>0$ and a noninverting reflection at its midpoint. A memoryless nonlinearity is a special case of an arbitrary time-varying gain [449]. By hypothesis, this gain has magnitude less than one. By routing the output of the delay line back to its input, the gain plays the role of a reflectance $ g$ at the ``other end'' of the ideal string or acoustic pipe. We can imagine, for example, a terminating dashpot with randomly varying positive resistance $ \mu(t)>0$. The set of all $ \mu>0$ corresponds to the set of real reflection coefficients $ g=(\mu-R)/(\mu+R)$ in the open interval $ (-1,1)$. Thus, each instantaneous nonlinearity-gain $ -1<g<1$ corresponds to some instantaneously positive resistance $ \mu>0$. The whole system is therefore passive, even as $ \mu(t)$ changes arbitrarily (while remaining positive). (It is perhaps easier to ponder a charged capacitor $ C$ terminated on a randomly varying resistor $ R(t)$.) This proof method immediately extends to nonlinear feedback around any transfer function that can be interpreted as the reflectance of a passive physical system, i.e., any transfer function $ H(s)$ for which the gain is bounded by 1 at each frequency, viz., $ \vert H(j\omega)\vert\le 1$.

The finite-sampling-rate case can be embedded in a passive infinite-sampling-rate case by replacing each sample with a constant pulse lasting $ T$ seconds (in the delay line). The continuous-time memoryless nonlinearity $ g[x(t)]$ is similarly a held version of the discrete-time case $ g[x(nT)]$. Since the discrete-time case is a simple sampling of the (passive) continuous-time case, we are done.

Practical Advice

In summary, the following pointers can be offered regarding nonlinear elements in a digital waveguide model:

  • Verify that aliasing can be heard and sounds bad before working to get rid of it.

  • Aliasing (bandwidth expansion) is reduced by smoothing ``corners'' in the nonlinearity.

  • Consider an oversampling factor for nonlinear subsystems sufficient to accommodate the bandwidth expansion caused by the nonlinearity.

  • Make sure there is adequate lowpass filtering in a feedback loop containing a nonlinearity.

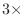As a specific example, consider the cubic nonlinearity used in a feedback loop (as in §9.1.6). This can be done with no aliasing at low levels (i.e., at levels below hard clipping) provided we use To avoid $ 3\times$ oversampling in the entire feedback loop, we may downsample by 3 after the lowpass filter and upsample by 3 just before the nonlinearity. If the lowpass filter is good, the downsampling by 3 is trivially accomplished by throwing away every 2 out of 3 samples. For upsampling, however, an additional third-band lowpass-filter is needed for the interpolation (§4.4).

Another variation is to oversample by two, in which case there is aliasing, but that aliasing does not reach the ``base band.'' Therefore, a half-band lowpass filter rejects both the second spectral image and the third, which is aliased onto the second.

Next Section:
Impedance
Previous Section:
String Coupling Effects