String Coupling Effects
It turns out that a single digital waveguide provides a relatively static-sounding string synthesizer. This is because several coupling mechanisms exist in natural string instruments. The overtones in coupled strings exhibit more interesting amplitude envelopes over time. Coupling between different strings is not the only important coupling phenomenon. In a real string, there are two orthogonal planes of transverse vibration which are intrinsically coupled to each other [181]. There is also intrinsic coupling between transverse vibrational waves and longitudinal waves (see §B.6).
Horizontal and Vertical Transverse Waves
The transverse waves considered up to now represent string vibration
only in a single two-dimensional plane. One such plane can be chosen
as being perpendicular to the top plate of a stringed musical instrument. We
will call this the ![]() plane and refer to it as the vertical
plane of polarization for transverse waves on a string (or simply the
vertical component of the transverse vibration). To more fully
model a real vibrating string, we also need to include transverse waves
in the
plane and refer to it as the vertical
plane of polarization for transverse waves on a string (or simply the
vertical component of the transverse vibration). To more fully
model a real vibrating string, we also need to include transverse waves
in the ![]() plane, i.e., a horizontal plane of polarization (or
horizontal component of vibration). Any polarization for transverse
traveling waves can be represented as a linear combination of
horizontal and vertical polarizations, and general transverse string
vibration in 3D can be expressed as a linear superposition of
vibration in any two distinct polarizations.
plane, i.e., a horizontal plane of polarization (or
horizontal component of vibration). Any polarization for transverse
traveling waves can be represented as a linear combination of
horizontal and vertical polarizations, and general transverse string
vibration in 3D can be expressed as a linear superposition of
vibration in any two distinct polarizations.
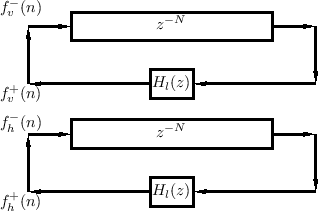 |
If string terminations were perfectly rigid, the horizontal polarization would be largely independent of the vertical polarization, and an accurate model would consist of two identical, uncoupled, filtered delay loops (FDL), as depicted in Fig.6.19. One FDL models vertical force waves while the other models horizontal force waves. This model neglects the small degree of nonlinear coupling between horizontal and vertical traveling waves along the length of the string--valid when the string slope is much less than unity (see §B.6).
Note that the model for two orthogonal planes of vibration on a single string is identical to that for a single plane of vibration on two different strings.
Coupled Horizontal and Vertical Waves
No vibrating string in musical acoustics is truly rigidly terminated, because such a string would produce no sound through the body of the instrument.7.15Yielding terminations result in coupling of the horizontal and vertical planes of vibration. In typical acoustic stringed instruments, nearly all of this coupling takes place at the bridge of the instrument.
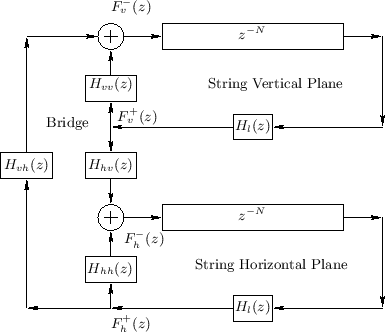 |
Figure 6.20 illustrates the more realistic case of
two planes of vibration which are linearly coupled at one end
of the string (the ``bridge''). Denoting the traveling force waves
entering the bridge from the vertical and horizontal vibration
components by ![]() and
and ![]() , respectively, the outgoing
waves in each plane are given by
, respectively, the outgoing
waves in each plane are given by
as shown in the figure.
In physically symmetric situations, we expect
![]() .
That is, the transfer function from horizontal to vertical waves is
normally the same as the transfer function from vertical to horizontal
waves.
.
That is, the transfer function from horizontal to vertical waves is
normally the same as the transfer function from vertical to horizontal
waves.
If we consider a single frequency ![]() , then the coupling matrix
with
, then the coupling matrix
with
![]() is a constant (generally complex) matrix (where
is a constant (generally complex) matrix (where
![]() denotes the sampling interval as usual). An eigenanalysis
of this matrix gives information about the modes of the coupled
system and the damping and tuning of these modes
[543].
denotes the sampling interval as usual). An eigenanalysis
of this matrix gives information about the modes of the coupled
system and the damping and tuning of these modes
[543].
As a simple example, suppose the coupling matrix
![]() at some frequency
has the form
at some frequency
has the form
![$\displaystyle \mathbf{H}(e^{j\omega T}) = \left[\begin{array}{cc} A & B \\ [2pt] B & A \end{array}\right]
$](http://www.dsprelated.com/josimages_new/pasp/img1497.png)
![$\displaystyle \underline{e}_1 = \left[\begin{array}{c} 1 \\ [2pt] 1 \end{array}...
...uad
\underline{e}_2 = \left[\begin{array}{c} 1 \\ [2pt] -1 \end{array}\right],
$](http://www.dsprelated.com/josimages_new/pasp/img1498.png)
The eigenvector
![]() corresponds to ``in phase'' vibration
of the two string endpoints, i.e.,
corresponds to ``in phase'' vibration
of the two string endpoints, i.e.,
![]() ,
while
,
while
![]() corresponds to ``opposite phase'' vibration, for
which
corresponds to ``opposite phase'' vibration, for
which
![]() . If it happens to be the case
that
. If it happens to be the case
that
More generally, the two eigenvectors of the coupling frequency-response matrix
![$\displaystyle \mathbf{H}(e^{j\omega}) \isdef \left[\begin{array}{cc} H_{vv}(e^{...
...\omega}) \\ [2pt] H_{hv}(e^{j\omega}) & H_{hh}(e^{j\omega}) \end{array}\right]
$](http://www.dsprelated.com/josimages_new/pasp/img1506.png)
By definition of the eigenvectors of
![]() , we have
, we have
TheIn particular, the modulus of the eigenvalue gives the reflectance magnitude (affecting mode damping), and the angle of the eigenvalue is the phase shift of the reflection, for that mode (affecting tuning of the mode). Use of coupling matrix eigenanalysis to determine mode damping and tuning is explored further in §C.13.th eigenvalue of the coupling matrix equals the frequency response seen by the
th eigenpolarization.
Asymmetry of Horizontal/Vertical Terminations
It is common in real stringed instruments that horizontal and vertical
transverse waves are transduced differently at the bridge. For
example, the bridge on a guitar is typically easier to ``push'' into
the top plate than it is to ``shear'' sidewise along the top plate.
In terms of Eq.![]() (6.16), we have
(6.16), we have
![]() (at most frequencies). This
unequal terminating impedance causes the horizontal component of
string vibration to decay slower than the vertical component of
vibration. We can say that this happens because the vertical bridge
admittance is much greater than the horizontal admittance, giving rise
to a faster rate of energy transfer from the vertical string
polarization into the bridge--in other words, the bridge is more
``yielding'' in the vertical direction. The audible consequence of
this unequal rate of decay is a two-stage amplitude envelope.
The initial fast decay gives a strong onset to the note, while the
slower late decay provides a long-lasting sustain--two normally
opposing but desirable features.
(at most frequencies). This
unequal terminating impedance causes the horizontal component of
string vibration to decay slower than the vertical component of
vibration. We can say that this happens because the vertical bridge
admittance is much greater than the horizontal admittance, giving rise
to a faster rate of energy transfer from the vertical string
polarization into the bridge--in other words, the bridge is more
``yielding'' in the vertical direction. The audible consequence of
this unequal rate of decay is a two-stage amplitude envelope.
The initial fast decay gives a strong onset to the note, while the
slower late decay provides a long-lasting sustain--two normally
opposing but desirable features.
Coupled Strings
We have just discussed the coupling between vertical and horizontal planes of vibration along a single string. There is also important coupling among different strings on the same instrument. For example, modern pianos are constructed having up to three physical strings associated with each key. These strings are slightly mistuned in order to sculpt the shape of the decay envelope, including its beating characteristics and two-stage decay. A two-stage decay is desired in piano strings in order to provide a strong initial attack followed by a long-sustaining ``aftersound'' [543], [18, Weinreich chapter].
A simple approximation to the effect of coupled strings is obtained by simply summing two or more slightly detuned strings. While this can provide a realistic beating effect in the amplitude envelope, it does not provide a true two-stage decay. A more realistic simulation of coupling requires signal to flow from each coupled string into all others.
When the bridge moves in response to string vibrations, traveling waves are generated along all other strings attached to the bridge. In the simplest case of a bridge modeled as a rigid body, the generated wave is identical on all strings. In §C.13, an efficient scattering formulation of string coupling at a bridge is derived for this case [439]. It can be seen as a simplification of the general coupling matrix shown in Fig.6.20 for the two-string (or two-polarization) case. Additionally, an eigenanalysis of the coupling matrix is performed, thereby extending the analysis of §6.12.2 above.
Longitudinal Waves
In addition to transverse waves on a string, there are always longitudinal waves present as well. In fact, longitudinal waves hold all of the potential energy associated with the transverse waves, and they carry the forward momentum in the direction of propagation associated with transverse traveling waves [122,391]. Longitudinal waves in a string typically travel an order of magnitude faster than transverse waves on the same string and are only weakly affected by changes in string tension.
Longitudinal waves are often neglected, e.g., in violin acoustics, because they couple inefficiently to the body through the bridge, and because they are ``out of tune'' anyway. However, there exist stringed instruments, such as the Finnish Kantele [231], in which longitudinal waves are too important to neglect. In the piano, longitudinal waves are quite audible; to bring this out in a striking way, sound example 5 provided in [18, Conklin chapter] plays Yankee Doodle on the longitudinal modes of three piano strings all tuned to the same (transversal) pitch. The nonlinear nature of the coupling from transverse to longitudinal waves has been demonstrated in [163]. Longitudinal waves have been included in some piano synthesis models [30,28,24,23].
Next Section:
Nonlinear Elements
Previous Section:
Loop Filter Identification








![$\displaystyle \left[\begin{array}{c} F_v^-(z) \\ [2pt] F_h^-(z) \end{array}\rig...
...] \left[\begin{array}{c} F_v^+(z) \\ [2pt] F_h^+(z) \end{array}\right] \protect$](http://www.dsprelated.com/josimages_new/pasp/img1494.png)











