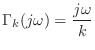Impedance
Impedance is defined for mechanical systems as
force divided by velocity, while the inverse (velocity/force) is
called an admittance. For dynamic systems, the impedance of a
``driving point'' is defined for each frequency ![]() , so that the
``force'' in the definition of impedance is best thought of as the
peak amplitude of a sinusoidal applied force, and similarly for the
velocity. Thus, if
, so that the
``force'' in the definition of impedance is best thought of as the
peak amplitude of a sinusoidal applied force, and similarly for the
velocity. Thus, if ![]() denotes the Fourier transform of the
applied force at a driving point, and
denotes the Fourier transform of the
applied force at a driving point, and ![]() is the Fourier
transform of the resulting velocity of the driving point, then the
driving-point impedance is given by
is the Fourier
transform of the resulting velocity of the driving point, then the
driving-point impedance is given by
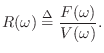
In acoustics [317,318], force takes the form of
pressure
(e.g., in physical units of newtons per meter squared),
and velocity may be either particle velocity in open air
(meters per second) or volume velocity in acoustic tubes
(meters cubed per second) (see §B.7.1 for
definitions).
The wave impedance (also called the characteristic
impedance) in open air is the ratio of pressure to particle velocity
in a sound wave traveling through air, and it is given by
![]() , where
, where ![]() is the density (mass
per unit volume) of air,
is the density (mass
per unit volume) of air, ![]() is the speed of sound propagation,
is the speed of sound propagation, ![]() is ambient pressure, and
is ambient pressure, and
![]() is the ratio of the specific
heat of air at constant pressure to that at constant volume. In a
vibrating string, the wave impedance is given by
is the ratio of the specific
heat of air at constant pressure to that at constant volume. In a
vibrating string, the wave impedance is given by
![]() , where
, where ![]() is string density (mass per unit length) and
is string density (mass per unit length) and ![]() is
the tension of the string (stretching force), as discussed further in
§C.1 and §B.5.2.
is
the tension of the string (stretching force), as discussed further in
§C.1 and §B.5.2.
In circuit theory [110], force takes the form of electric
potential in volts, and velocity manifests as electric current in amperes
(coulombs per second). In an electric transmission line, the
characteristic impedance is given by
![]() where
where ![]() and
and ![]() are the inductance and capacitance, respectively, per unit length along the
transmission line. In free space, the wave impedance for light is
are the inductance and capacitance, respectively, per unit length along the
transmission line. In free space, the wave impedance for light is
![]() , where
, where ![]() and
and
![]() are
the permeability and permittivity, respectively, of free space. One might
be led from this to believe that there must exist a medium, or `ether',
which sustains wave propagation in free space; however, this is one
instance in which ``obvious'' predictions from theory turn out to be wrong.
are
the permeability and permittivity, respectively, of free space. One might
be led from this to believe that there must exist a medium, or `ether',
which sustains wave propagation in free space; however, this is one
instance in which ``obvious'' predictions from theory turn out to be wrong.
Dashpot
The elementary impedance element in mechanics is the dashpot which
may be approximated mechanically by a plunger in a cylinder of air or
liquid, analogous to a shock absorber for a car. A constant impedance
means that the velocity produced is always linearly proportional to the
force applied, or
![]() , where
, where ![]() is the dashpot impedance,
is the dashpot impedance,
![]() is the applied force at time
is the applied force at time ![]() , and
, and ![]() is the velocity. A
diagram is shown in Fig. 7.1.
is the velocity. A
diagram is shown in Fig. 7.1.
![\includegraphics[scale=0.9]{eps/ldashpot}](http://www.dsprelated.com/josimages_new/pasp/img1569.png) |
In circuit theory, the element analogous to the dashpot is the
resistor ![]() , characterized by
, characterized by
![]() , where
, where ![]() is voltage
and
is voltage
and ![]() is current. In an analog equivalent circuit, a dashpot can be
represented using a resistor
is current. In an analog equivalent circuit, a dashpot can be
represented using a resistor ![]() .
.
Over a specific velocity range, friction force can also be
characterized by the relation
![]() . However, friction is
very complicated in general [419], and as the velocity goes
to zero, the coefficient of friction
. However, friction is
very complicated in general [419], and as the velocity goes
to zero, the coefficient of friction ![]() may become much larger.
The simple model often presented is to use a static coefficient
of friction when starting at rest (
may become much larger.
The simple model often presented is to use a static coefficient
of friction when starting at rest (![]() ) and a dynamic
coefficient of friction when in motion (
) and a dynamic
coefficient of friction when in motion (
![]() ). However, these
models are too simplified for many practical situations in musical
acoustics, e.g., the frictional force between the bow and string of a
violin [308,549], or the internal friction losses
in a vibrating string [73].
). However, these
models are too simplified for many practical situations in musical
acoustics, e.g., the frictional force between the bow and string of a
violin [308,549], or the internal friction losses
in a vibrating string [73].
Ideal Mass
The concept of impedance extends also to masses and springs.
Figure 7.2 illustrates an ideal mass of ![]() kilograms
sliding on a frictionless surface. From Newton's second law of motion, we
know force equals mass times acceleration, or
kilograms
sliding on a frictionless surface. From Newton's second law of motion, we
know force equals mass times acceleration, or
Since impedance is defined in terms of force and velocity, we will prefer the
form
![]() . By the differentiation theorem for Laplace transforms
[284],8.1we have
. By the differentiation theorem for Laplace transforms
[284],8.1we have
Since we normally think of an applied force as an input and the resulting
velocity as an output, the corresponding transfer function is
![]() . The system diagram for this view
is shown in Fig. 7.3.
. The system diagram for this view
is shown in Fig. 7.3.
The impulse response of a mass, for a force input and velocity output, is defined as the inverse Laplace transform of the transfer function:
![\includegraphics[scale=0.9]{eps/lblackbox}](http://www.dsprelated.com/josimages_new/pasp/img1587.png) |
Once the input and output signal are defined, a transfer function is
defined, and therefore a frequency response is defined [485].
The frequency response is given by the transfer function evaluated on
the ![]() axis in the
axis in the ![]() plane, i.e., for
plane, i.e., for ![]() . For the ideal mass,
the force-to-velocity frequency response is
. For the ideal mass,
the force-to-velocity frequency response is
In circuit theory, the element analogous to the mass is the inductor,
characterized by
![]() , or
, or
![]() . In an analog
equivalent circuit, a mass can be represented using an inductor with value
. In an analog
equivalent circuit, a mass can be represented using an inductor with value
![]() .
.
Ideal Spring
Figure 7.4 depicts the ideal spring.
From Hooke's law, we have that the applied force is proportional to the displacement of the spring:
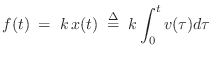
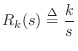
The frequency response of the ideal spring, given the applied force as input and resulting velocity as output, is
In this case, the amplitude response grows
We call ![]() the compression velocity of the spring. In more
complicated configurations, the compression velocity is defined as the
difference between the velocity of the two spring endpoints, with positive
velocity corresponding to spring compression.
the compression velocity of the spring. In more
complicated configurations, the compression velocity is defined as the
difference between the velocity of the two spring endpoints, with positive
velocity corresponding to spring compression.
In circuit theory, the element analogous to the spring is the capacitor,
characterized by
![]() , or
, or
![]() .
In an equivalent analog circuit, we can use the value
.
In an equivalent analog circuit, we can use the value ![]() . The
inverse
. The
inverse ![]() of the spring stiffness is sometimes called the
compliance
of the spring.
of the spring stiffness is sometimes called the
compliance
of the spring.
Don't forget that the definition of impedance requires zero initial conditions for elements with ``memory'' (masses and springs). This means we can only use impedance descriptions for steady state analysis. For a complete analysis of a particular system, including the transient response, we must go back to full scale Laplace transform analysis.
Next Section:
One-Port Network Theory
Previous Section:
Nonlinear Elements








![\includegraphics[scale=0.9]{eps/lmass}](http://www.dsprelated.com/josimages_new/pasp/img1575.png)
![\includegraphics[width=3in]{eps/lspring}](http://www.dsprelated.com/josimages_new/pasp/img1592.png)