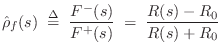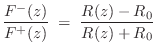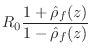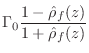Passive Reflectances
From Eq.![]() (C.75),
we have that the reflectance seen at a continuous-time impedance
(C.75),
we have that the reflectance seen at a continuous-time impedance
![]() is given for force waves by
is given for force waves by
where
In particular,
If the impedance ![]() goes to infinity (becomes rigid), then
goes to infinity (becomes rigid), then
![]() approaches
approaches ![]() , a result which agrees with an analysis of
rigid string terminations (p.
, a result which agrees with an analysis of
rigid string terminations (p. ![]() ). Similarly, when the
impedance goes to zero,
). Similarly, when the
impedance goes to zero,
![]() becomes
becomes ![]() , which agrees with
the physics of a string with a free end. In acoustic stringed
instruments, bridges are typically quite rigid, so that
, which agrees with
the physics of a string with a free end. In acoustic stringed
instruments, bridges are typically quite rigid, so that
![]() for all
for all ![]() . If a body resonance is
strongly coupled through the bridge,
. If a body resonance is
strongly coupled through the bridge,
![]() can be
significantly smaller than 1 at the resonant frequency
can be
significantly smaller than 1 at the resonant frequency ![]() .
.
Solving for ![]() in Eq.
in Eq.![]() (C.77), we can characterize every
impedance in terms of its reflectance:
(C.77), we can characterize every
impedance in terms of its reflectance:
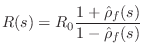
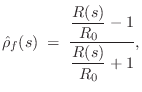
In the discrete-time case, which may be related to the continuous-time
case by the bilinear transform (§7.3.2), we have the same basic
relations, but in the ![]() plane:
plane:
where
Mathematically, any stable transfer function having these properties may be called a Schur function. Thus, the discrete-time reflectance
Note that Eq.![]() (C.79) may be obtained from the general formula for
scattering at a loaded waveguide junction for the case of a single
waveguide (
(C.79) may be obtained from the general formula for
scattering at a loaded waveguide junction for the case of a single
waveguide (![]() ) terminated by a lumped load (§C.12).
) terminated by a lumped load (§C.12).
In the limit as damping goes to zero (all poles of ![]() converge to
the unit circle),
the reflectance
converge to
the unit circle),
the reflectance
![]() becomes a digital allpass filter. Similarly,
becomes a digital allpass filter. Similarly,
![]() becomes a continuous-time allpass filter as the poles of
becomes a continuous-time allpass filter as the poles of
![]() approach the
approach the ![]() axis.
axis.
Recalling that a lossless impedance is called a reactance
(§7.1), we can say that every reactance gives rise to an
allpass reflectance. Thus, for example, waves reflecting off a
mass at the end of a vibrating string will be allpass filtered,
because the driving-point impedance of a mass (![]() ) is a pure
reactance. In particular, the force-wave reflectance of a mass
) is a pure
reactance. In particular, the force-wave reflectance of a mass ![]() terminating an ideal string having wave impedance
terminating an ideal string having wave impedance ![]() is
is
![]() , which is a continuous-time allpass filter having
a pole at
, which is a continuous-time allpass filter having
a pole at ![]() and a zero at
and a zero at ![]() .
.
It is intuitively reasonable that a passive reflection gain cannot
exceed ![]() at any frequency (i.e., the reflectance is a Schur filter,
as defined in Eq.
at any frequency (i.e., the reflectance is a Schur filter,
as defined in Eq.![]() (C.79)). It is also reasonable that lossless
reflection would have a gain of 1 (i.e., it is allpass).
(C.79)). It is also reasonable that lossless
reflection would have a gain of 1 (i.e., it is allpass).
Note that reflection filters always have an equal number of poles and
zeros, as can be seen from Eq.![]() (C.76) above. This property is
preserved by the bilinear transform, so it holds in both the
continuous- and discrete-time cases.
(C.76) above. This property is
preserved by the bilinear transform, so it holds in both the
continuous- and discrete-time cases.
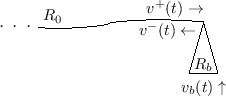
Reflectance and Transmittance of a Yielding String Termination
Consider the special case of a reflection and transmission at a
yielding termination, or ``bridge'', of an ideal vibrating
string on its right end, as shown in Fig.C.28. Denote the
incident and reflected velocity waves by ![]() and
and ![]() ,
respectively, and similarly denote the force-wave components by
,
respectively, and similarly denote the force-wave components by
![]() and
and
![]() . Finally, denote the velocity of the
termination itself by
. Finally, denote the velocity of the
termination itself by
![]() , and its force-wave
reflectance by
, and its force-wave
reflectance by

The bridge velocity is given by
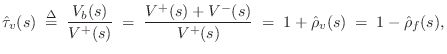
![$\displaystyle \hat{\tau}_f(s) \isdefs \frac{F_b(s)}{F^{+}(s)}
\eqsp \frac{R_0[V^{+}(s)-V^{-}(s)]}{R_0V^{+}(s)}
\eqsp 1+\hat{\rho}_f(s)
$](http://www.dsprelated.com/josimages_new/pasp/img3757.png)
Power-Complementary Reflection and Transmission
We can show that the reflectance and transmittance of the yielding termination are power complementary. That is, the reflected and transmitted signal-power sum to yield the incident signal-power.
The average power incident at the bridge at frequency ![]() can be
expressed in the frequency domain as
can be
expressed in the frequency domain as
![]() .
The reflected power is then
.
The reflected power is then
![]() . Removing the minus sign, which can be
associated with reversed direction of travel, we obtain that the
power reflection frequency response is
. Removing the minus sign, which can be
associated with reversed direction of travel, we obtain that the
power reflection frequency response is
![]() , which
generalizes by analytic continuation to
, which
generalizes by analytic continuation to
![]() . The power
transmittance is given by
. The power
transmittance is given by
Next Section:
Positive Real Functions
Previous Section:
Reflectance of an Impedance