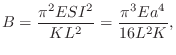Stiff Piano Strings
Piano strings are audibly inharmonic due to stiffness [211,210]. General stiff-string modeling was introduced in §6.9. In this section, we discuss further details specific to piano strings.
The main effect of string stiffness is to stretch the partial overtone series, so that piano tones are not precisely harmonic [144]. As a result, piano tuners typically stretch the tuning of the piano slightly. For example, the total amount of tuning stretch from the lowest to highest note has been measured to be approximately 35 cents on a Kurzweil PC88, 45 cents on a Steinway Model M, and 60 cents on a Steinway Model D.10.17
Piano String Wave Equation
A wave equation suitable for modeling linearized piano strings is given by [77,45,317,517]
where the partial derivative notation

Young's modulus and the radius of gyration are defined in Appendix B.
The first two terms on the right-hand side of Eq.![]() (9.30) come from
the ideal string wave equation (see Eq.
(9.30) come from
the ideal string wave equation (see Eq.![]() (C.1)), and they model
transverse acceleration and transverse restoring force due to tension,
respectively. The term
(C.1)), and they model
transverse acceleration and transverse restoring force due to tension,
respectively. The term ![]() approximates the transverse
restoring force exerted by a stiff string when it is bent. In an
ideal string with zero diameter, this force is zero; in an ideal
rod (or bar), this term is dominant [317,261,169].
The final two terms provide damping. The damping associated
with
approximates the transverse
restoring force exerted by a stiff string when it is bent. In an
ideal string with zero diameter, this force is zero; in an ideal
rod (or bar), this term is dominant [317,261,169].
The final two terms provide damping. The damping associated
with ![]() is frequency-independent, while the damping due
is frequency-independent, while the damping due ![]() increases with frequency.
increases with frequency.
Damping-Filter Design
In [46], the damping in real piano strings was modeled using a length 17 FIR filter for the lowest strings, and a length 9 FIR filter for the remaining strings. Such FIR filters (or nonparametric measured frequency-response data) can be converted to lower-order IIR filters by the usual methods (§8.6.2). It is convenient to have separate damping and dispersion filters in the string model. The damping filter in piano strings is significantly less demanding than the dispersion filter.
Dispersion Filter-Design
In the context of a digital waveguide string model, dispersion associated with stiff strings can be supplied by an allpass filter in the basic feedback loop. Methods for designing dispersion allpass filters were summarized in §6.11.3. In this section, we are mainly concerned with how to specify the desired dispersion allpass filter for piano strings.
Perceptual studies regarding the audibility of inharmonicity in stringed instrument sounds [211] indicate that the just noticeable coefficient of inharmonicity is given approximately by
where
For a stiff string with Young's modulus
where
In general, when designing dispersion filters for vibrating string models, it is highly cost-effective to obtain an allpass filter which correctly tunes only the lowest-frequency partial overtones, where the number of partials correctly tuned is significantly less than the total number of partials present, as in [384].
Application of the method of [2] to piano-string dispersion-filter design is reported in [1].
A Faust implementation of a closed-form expression
[367] for dispersion allpass coefficients as a
function of inharmonicity coefficient ![]() may be found in the function
piano_dispersion_filter within effect.lib.
may be found in the function
piano_dispersion_filter within effect.lib.
Next Section:
Nonlinear Piano Strings
Previous Section:
Pluck Modeling