The Externally Excited String

Free Books Physical Audio Signal Processing

Sections 6.5 and 6.6 illustrated plucking or striking the string by means of initial conditions: an initial displacement for plucking and an initial velocity distribution for striking. Such a description parallels that found in many textbooks on acoustics, such as [317]. However, if the string is already in motion, as it often is in normal usage, it is more natural to excite the string externally by the equivalent of a ``pick'' or ``hammer'' as is done in the real world instrument.

Figure 6.14 depicts a rigidly terminated string with an external excitation input. The wave variable can be set to acceleration, velocity, or displacement, as appropriate. (Choosing force waves would require eliminating the sign inversions at the terminations.) The external input is denoted ${\Delta w}$ to indicate that it is an additive incremental input, superimposing with the existing string state.

**Figure 6.14:** Discrete simulation of the rigidly terminated string with an external excitation.
$\includegraphics[width=\twidth]{eps/fpluckedstring}$

For idealized plucked strings, we may take (acceleration), and ${\Delta w}$ can be a single nonzero sample, or impulse, at the plucking instant. As always, bandlimited interpolation can be used to provide a non-integer time or position. In the latter case, there would be two or more summers along both the upper and lower rails, separated by unit delays. More generally, the string may be plucked by a force distribution . The applied force at a point can be translated to the corresponding velocity increment via the wave impedance :

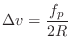$\displaystyle \Delta v = \frac{f_p}{2R}$

(7.15)

where $R=\sqrt{K\epsilon }$ as before. The factor of two comes from the fact that two string endpoints are being driven physically in parallel. (Physically, they are in parallel, but as impedances, they are formally in series. See §7.2 for the theory.)

Note that the force applied by a rigid, stationary pick or hammer varies with the state of a vibrating string. Also, when a pick or hammer makes contact with the string, it partially terminates the string, resulting in reflected waves in each direction. A simple model for the termination would be a mass affixed to the string at the excitation point. (This model is pursued in §9.3.1.) A more general model would be an arbitrary impedance and force source affixed to the string at the excitation point during the excitation event. This is a special case of the ``loaded waveguide junction,'' discussed in §C.12. In the waveguide model for bowed strings (§9.6), the bow-string interface is modeled as a nonlinear scattering junction.

Equivalent Forms

In a physical piano string, as a specific example, the hammer strikes the string between its two inputs, some distance from the agraffe and far from the bridge. This corresponds to the diagram in Fig.6.15, where the delay lines are again arranged for clarity of physical interpretation. Figure 6.15 is almost identical to Fig.6.14, except that the delay lines now contain samples of traveling force waves, and the bridge is allowed to vibrate, resulting in a filtered reflection at the bridge (see §9.2.1 for a derivation of the bridge filter). The hammer-string interaction force-pulse is summed into both the left- and right-going delay lines, corresponding to sending the same pulse toward both ends of the string from the hammer. Force waves are discussed further in §C.7.2.

**Figure 6.15:** Model of a piano string struck in its interior by a hammer.
$\includegraphics[width=\twidth]{eps/pianoInteriorStringExcitation}$

**Figure:** Diagram equivalent to Fig.6.15, obtained by combining upper- and lower-rail delay lines.
$\includegraphics[width=\twidth]{eps/pianoSimplifiedInteriorStringExcitation}$

By commutativity of linear, time-invariant elements, Figure 6.15 can be immediately simplified to the form shown in Fig.6.16, in which each delay line corresponds to the travel time in both directions on each string segment. From a structural point of view, we have a conventional filtered delay loop plus a second input which sums into the loop somewhere inside the delay line. The output is shown coming from the middle of the larger delay line, which gives physically correct timing, but in practice, the output can be taken from anywhere in the feedback loop. It is probably preferable in practice to take the output from the loop-delay-line input. That way, other response latencies in the overall system can be compensated.

**Figure:** Diagram equivalent to Fig.6.15, obtained by replacing the second string input by a separate comb-filter applied to a single input.
$\includegraphics[width=\twidth]{eps/pianoSimplifiedISEExtracted}$

An alternate structure equivalent to Fig.6.16 is shown in Fig.6.17, in which the second input injection is factored out into a separate comb-filtering of the input. The comb-filter delay equals the delay between the two inputs in Fig.6.16, and the delay in the feedback loop equals the sum of both delays in Fig.6.16. In this case, the string is modeled using a simple filtered delay loop, and the striking-force signal is separately filtered by a comb filter corresponding to the striking-point along the string.

Algebraic derivation

The above equivalent forms are readily verified by deriving the transfer function from the striking-force input to the output force signal

Referring to Fig.6.15, denote the input hammer-strike transform by and the output signal transform by . Also denote the loop-filter transfer function by . By inspection of the figure, we can write

$\displaystyle F_o(z) = z^{-N} \left\{ F_i(z) + z^{-2M}\left[F_i(z) + z^{-N} H_l(z)F_o(z)\right]\right\}.$

Solving for the input-output transfer function yields

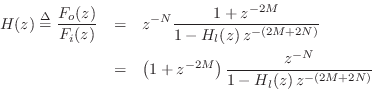
$\begin{eqnarray*} H(z) \isdef \frac{F_o(z)}{F_i(z)} &=& z^{-N} \frac{1+z^{-2M}}... ...& \left(1+z^{-2M}\right)\frac{z^{-N}}{1-H_l(z)\,z^{-(2M+2N)}}\\ \end{eqnarray*}$

The final factored form above corresponds to the final equivalent form shown in Fig.6.17.

Related Forms

We see from the preceding example that a filtered-delay loop (a feedback comb-filter using filtered feedback, with delay-line length in the above example) simulates a vibrating string in a manner that is independent of where the excitation is applied. To simulate the effect of a particular excitation point, a feedforward comb-filter may be placed in series with the filtered delay loop. Such a ``pluck position'' illusion may be applied to any basic string synthesis algorithm, such as the EKS [428,207].

By an exactly analogous derivation, a single feedforward comb filter can be used to simulate the location of a linearized magnetic pickup [200] on a simulated electric guitar string. An ideal pickup is formally the transpose of an excitation. For a discussion of filter transposition (using Mason's gain theorem [301,302]), see, e.g., [333,449].^7.9

The comb filtering can of course also be implemented after the filtered delay loop, again by commutativity. This may be desirable in situations in which comb filtering is one of many options provided for in the ``effects section'' of a synthesizer. Post-processing comb filters are often used in reverberator design and in virtual pickup simulation.

**Figure 6.18:** Use of a second delay-line tap to implement comb filtering corresponding to hammer-strike echoes returning from the far end of the string.
$\includegraphics[width=\twidth]{eps/pianoSecondStringTap}$

The comb-filtering can also be conveniently implemented using a second tap from the appropriate delay element in the filtered delay loop simulation of the string, as depicted in Fig.6.18. The new tap output is simply summed (or differenced, depending on loop implementation) with the filtered delay loop output. Note that making the new tap a moving, interpolating tap (e.g., using linear interpolation), a flanging effect is available. The tap-gain can be brought out as a musically useful timbre control that goes beyond precise physical simulation (e.g., it can be made negative). Adding more moving taps and summing/differencing their outputs, with optional scale factors, provides an economical chorus or Leslie effect. These extra delay effects cost no extra memory since they utilize the memory that's already needed for the string simulation. While such effects are not traditionally applied to piano sounds, they are applied to electric piano sounds which can also be simulated using the same basic technique.

Summary

In summary, two feedforward comb filters and one feedback comb filter arranged in series (in any order) can be interpreted as a physical model of a vibrating string driven at one point along the string and observed at a different point along the string. The two feedforward comb-filter delays correspond to the excitation and pickup locations along the string, while the amount of feedback-loop delay controls the fundamental frequency of vibration. A filter in the feedback loop determines the decay rate and fine tuning of the partial overtones.

Next Section:
Loop Filter Identification
Previous Section:
The Stiff String