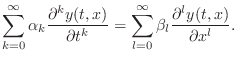Free Books
   Free Books    Physical Audio Signal Processing  

The Dispersive 1D Wave Equation

In the ideal vibrating string, the only restoring force for transverse displacement comes from the string tension (§C.1 above); specifically, the transverse restoring force is equal the net transverse component of the axial string tension. Consider in place of the ideal string a bundle of ideal strings, such as a stranded cable. When the cable is bent, there is now a new restoring force arising from some of the fibers being compressed and others being stretched by the bending. This force sums with that due to string tension. Thus, stiffness in a vibrating string introduces a new restoring force proportional to bending angle. It is important to note that string stiffness is a linear phenomenon resulting from the finite diameter of the string.

In typical treatments,C.3bending stiffness adds a new term to the wave equation that is proportional to the fourth spatial derivative of string displacement:

$\displaystyle \epsilon {\ddot y}= Ky''- \kappa y'''' \protect$ (C.32)

where the moment constant $ \kappa = YI$ is the product of Young's modulus $ Y$ (the ``relative-displacement spring constant per unit cross-sectional area,'' discussed in §B.5.1) and the area moment of inertia $ I$ (§B.4.8); as derived in §B.4.9, a cylindrical string of radius $ a$ has area moment of inertia equal to $ \pi a^2 \cdot (a/2)^2 = \pi a^4/4$. This wave equation works well enough for small amounts of bending stiffness, but it is clearly missing some terms because it predicts that deforming the string into a parabolic shape will incur no restoring force due to stiffness. See §6.9 for further discussion of wave equations for stiff strings. To solve the stiff wave equation Eq.$ \,$(C.32), we may set $ y(t,x) = e^{st+vx}$ to get

$\displaystyle \epsilon s^2 = Kv^2 - \kappa v^4. $

At very low frequencies, or when stiffness is negligible in comparison with $ K/v^2$, we obtain again the non-stiff string: $ \epsilon s^2\approx Kv^2 \,\,\Rightarrow\,\,v=\pm s/c$. At very high frequencies, or when the tension $ K$ is negligible relative to $ \kappa v^2$, we obtain the ideal bar (or rod) approximation:

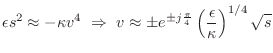
$\displaystyle \epsilon s^2 \approx -\kappa v^4 \,\,\Rightarrow\,\,v \approx \pm e^{\pm j\frac{\pi}{4}} \left(\frac{\epsilon }{\kappa} \right)^{1/4}\sqrt{s} $

In an ideal bar, the only restoring force is due to bending stiffness. Setting $ s=j\omega$ gives solutions $ v=\pm j\left( \epsilon /\kappa\right)^{1/4}\sqrt{\omega}$ and $ v=\pm\left( \epsilon /\kappa\right)^{1/4}\sqrt{\omega}$. In the first case, the wave velocity becomes proportional to $ \sqrt{\omega}$. That is, waves travel faster along the ideal bar as oscillation frequency increases, going up as the square root of frequency. The second solution corresponds to a change in the wave shape which prevents sharp corners from forming due to stiffness [95,118]. At intermediate frequencies, between the ideal string and the ideal bar, the stiffness contribution can be treated as a correction term [95]. This is the region of most practical interest because it is the principal operating region for strings, such as piano strings, whose stiffness has audible consequences (an inharmonic, stretched overtone series). Assuming $ \kappa_0 \isdeftext \kappa/K\ll 1$,
$\displaystyle s^2$ $\displaystyle =$ $\displaystyle \frac{K}{\epsilon } v^2 - \frac{\kappa}{\epsilon } v^4 = \frac{K}... ...(1 - \frac{\kappa}{K} v^2\right) \isdef c_0^2 v^2 \left(1 - \kappa_0 v^2\right)$  
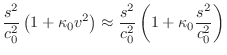$\displaystyle \,\,\Rightarrow\,\,v^2$ $\displaystyle \approx$ $\displaystyle \frac{s^2}{c_0^2} \left(1+\kappa_0 v^2\right) \approx \frac{s^2}{c_0^2} \left(1+\kappa_0 \frac{s^2}{c_0^2}\right)$  
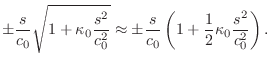$\displaystyle \,\,\Rightarrow\,\,v$ $\displaystyle \approx$ $\displaystyle \pm \frac{s}{c_0} \sqrt{1+\kappa_0 \frac{s^2}{c_0^2}} \approx \pm \frac{s}{c_0} \left(1+\frac{1}{2}\kappa_0 \frac{s^2}{c_0^2} \right).$  

Substituting for $ v$ in terms of $ s$ in $ e^{st+vx}$ gives the general eigensolution

$\displaystyle e^{st+vx} = \exp{\left\{{s\left[t\pm \frac{x}{c_0}\left( 1+\frac{1}{2}\kappa_0 \frac{s^2}{c_0^2} \right)\right]}\right\}}. $

Setting $ s=j\omega$ as before, corresponding to driving the medium sinusoidally over time at frequency $ \omega $, the medium response is

$\displaystyle e^{st+vx} = e^{j\omega\left[t\pm {x/ c(\omega)}\right]} $

where

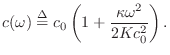
$\displaystyle c(\omega) \isdef c_0\left(1 + \frac{\kappa\omega^2}{2Kc_0^2}\right). $

Because the effective wave velocity depends on $ \omega $, we cannot use Fourier's theorem to construct arbitrary traveling shapes by superposition. At $ x=0$, we can construct any function of time, but the waveshape disperses as it propagates away from $ x=0$. The higher-frequency Fourier components travel faster than the lower-frequency components. Since the temporal and spatial sampling intervals are related by $ X=cT$, this must generalize to $ X= c(\omega)T\,\,\Rightarrow\,\, T(\omega)=X/c(\omega)=c_0T_0/c(\omega)$, where $ T_0=T(0)$ is the size of a unit delay in the absence of stiffness. Thus, a unit delay $ z^{-1}$ may be replaced by

$\displaystyle z^{-1}\to z^{-c_0/c(\omega)}$   (for frequency-dependent wave velocity).

That is, each delay element becomes an allpass filter which approximates the required delay versus frequency. A diagram appears in Fig.C.8, where $ H_a(z)$ denotes the allpass filter which provides a rational approximation to $ z^{-c_0/c(\omega)}$.
Figure C.8: Section of a stiff string where allpass filters play the role of unit delay elements.
\includegraphics[scale=0.9]{eps/fstiffstring}
The general, order $ L$, allpass filter is given by [449]

$\displaystyle H_a(z) \isdef z^{-L} {A(z^{-1})/A(z)} $

where

$\displaystyle A(z) \isdef 1 + a_1 z^{-1}+ a_2 z^{-2} + \cdots + a_L z^{-L} $

and the roots of $ A(z)$ must all have modulus less than $ 1$. That is, the numerator polynomial is just the reverse of the denominator polynomial. This implies each pole $ p_i$ is gain-compensated by a zero at $ z_i=1/p_i$. For computability of the string simulation in the presence of scattering junctions, there must be at least one sample of pure delay along each uniform section of string. This means for at least one allpass filter in Fig.C.8, we must have $ H_a(\infty)=0$ which implies $ H_a(z)$ can be factored as $ z^{-1}H_a'(z)$. In a systolic VLSI implementation, it is desirable to have at least one real delay from the input to the output of every allpass filter, in order to be able to pipeline the computation of all of the allpass filters in parallel. Computability can be arranged in practice by deciding on a minimum delay, (e.g., corresponding to the wave velocity at a maximum frequency), and using an allpass filter to provide excess delay beyond the minimum. Because allpass filters are linear and time invariant, they commute like gain factors with other linear, time-invariant components. Fig.C.9 shows a diagram equivalent to Fig.C.8 in which the allpass filters have been commuted and consolidated at two points. For computability in all possible contexts (e.g., when looped on itself), a single sample of delay is pulled out along each rail. The remaining transfer function, $ H_c(z) = z H_a^3(z)$ in the example of Fig.C.9, can be approximated using any allpass filter design technique [1,2,267,272,551]. Alternatively, both gain and dispersion for a stretch of waveguide can be provided by a single filter which can be designed using any general-purpose filter design method which is sensitive to frequency-response phase as well as magnitude; examples include equation error methods (such as used in the matlab invfreqz function (§8.6.4), and Hankel norm methods [177,428,36].
Figure C.9: Section of a stiff string where the allpass delay elements are consolidated at two points, and a sample of pure delay is extracted from each allpass chain.
\includegraphics[scale=0.9]{eps/flstiffstring}
In the case of a lossless, stiff string, if $ H_c(z)$ denotes the consolidated allpass transfer function, it can be argued that the filter design technique used should minimize the phase-delay error, where phase delay is defined by [362]

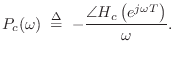$\displaystyle P_c(\omega) \isdefs - \frac{\angle H_c\left(e^{j\omega T}\right)}{\omega}.$   (Phase Delay)

Minimizing the Chebyshev norm of the phase-delay error,

$\displaystyle \vert\vert\,P_c(\omega)-c_0/c(\omega)\,\vert\vert _\infty $

approximates minimization of the error in mode tuning for the freely vibrating string [428, pp. 182-184]. Since the stretching of the overtone series is typically what we hear most in a stiff, vibrating string, the worst-case phase-delay error is a good choice in such a case. Alternatively, a lumped allpass filter can be designed by minimizing group delay,

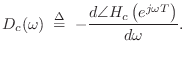$\displaystyle D_c(\omega) \isdefs - \frac{ d\angle H_c\left(e^{j\omega T}\right)}{d\omega}.$   (Group Delay)

The group delay of a filter gives the delay experienced by the amplitude envelope of a narrow frequency band centered at $ \omega $, while the phase delay applies to the ``carrier'' at $ \omega $, or a sinusoidal component at frequency $ \omega $ [342]. As a result, for proper tuning of overtones, phase delay is what matters, while for precisely estimating (or controlling) the decay time in a lossy waveguide, group delay gives the effective filter delay ``seen'' by the exponential decay envelope. See §9.4.1 for designing allpass filters with a prescribed delay versus frequency. To model stiff strings, the allpass filter must supply a phase delay which decreases as frequency increases. A good approximation may require a fairly high-order filter, adding significantly to the cost of simulation. (For low-pitched piano strings, order 8 allpass filters work well perceptually [1].) To a large extent, the allpass order required for a given error tolerance increases as the number of lumped frequency-dependent delays is increased. Therefore, increased dispersion consolidation is accompanied by larger required allpass filters, unlike the case of resistive losses. The function piano_dispersion_filter in the Faust distribution (in effect.lib) designs and implements an allpass filter modeling the dispersion due to stiffness in a piano string [154,170,368].

Higher Order Terms

The complete, linear, time-invariant generalization of the lossy, stiff string is described by the differential equation

$\displaystyle \sum_{k=0}^\infty \alpha_k \frac{\partial^k y(t,x)}{\partial t^k} = \sum_{l=0}^\infty \beta_l \frac{\partial^l y(t,x)}{\partial x^l}. \protect$ (C.33)

which, on setting $ y(t,x) = e^{st+vx}$, (or taking the 2D Laplace transform with zero initial conditions), yields the algebraic equation,

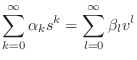$\displaystyle \sum_{k=0}^\infty \alpha_k s^k = \sum_{l=0}^\infty \beta_l v^l$ (C.34)

Solving for $ v$ in terms of $ s$ is, of course, nontrivial in general. However, in specific cases, we can determine the appropriate attenuation per sample $ G(\omega)$ and wave propagation speed $ c(\omega)$ by numerical means. For example, starting at $ s=0$, we normally also have $ v=0$ (corresponding to the absence of static deformation in the medium). Stepping $ s$ forward by a small differential $ j{{\Delta}}\omega $, the left-hand side can be approximated by $ \alpha_0+\alpha_1j{{\Delta}}\omega $. Requiring the generalized wave velocity $ s/v(s)$ to be continuous, a physically reasonable assumption, the right-hand side can be approximated by $ \beta_0+\beta_1 \Delta v$, and the solution is easy. As $ s$ steps forward, higher order terms become important one by one on both sides of the equation. Each new term in $ v$ spawns a new solution for $ v$ in terms of $ s$, since the order of the polynomial in $ v$ is incremented. It appears possible that homotopy continuation methods [316] can be used to keep track of the branching solutions of $ v$ as a function of $ s$. For each solution $ v(s)$, let $ {v_r}(\omega)$ denote the real part of $ v(j\omega)$ and let $ {v_i}(\omega)$ denote the imaginary part. Then the eigensolution family can be seen in the form $ \exp{\left\{j\omega t\pm v(j\omega)x\right\}}=\exp{\left\{\pm{v_r}(\omega)x\right\}}\cdot\exp{\left\{j\omega\left(t \pm {v_i}(\omega)x/\omega\right)\right\}}$. Defining $ c(\omega)\isdeftext \omega/{v_i}(\omega)$, and sampling according to $ x\to x_m\isdeftext mX$ and $ t\to t_n\isdeftext nT(\omega)$, with $ X\isdeftext c(\omega)T(\omega)$ as before, (the spatial sampling period is taken to be frequency invariant, while the temporal sampling interval is modulated versus frequency using allpass filters), the left- and right-going sampled eigensolutions become
$\displaystyle e^{j\omega t_n\pm v(j\omega)x_m}$ $\displaystyle =$ $\displaystyle e^{\pm{v_r}(\omega)x_m}\cdot e^{ j\omega\left(t_n\pm x_m/c(\omega)\right)}$ (C.35)
  $\displaystyle =$ $\displaystyle G^m(\omega)\cdot e^{ j\omega\left(n \pm m\right)T(\omega)}$  

where $ G(\omega)\isdef e^{\pm{v_r}(\omega)X}$. Thus, a general map of $ v$ versus $ s$, corresponding to a partial differential equation of any order in the form (C.33), can be translated, in principle, into an accurate, local, linear, time-invariant, discrete-time simulation. The boundary conditions and initial state determine the initial mixture of the various solution branches as usual. We see that a large class of wave equations with constant coefficients, of any order, admits a decaying, dispersive, traveling-wave type solution. Even-order time derivatives give rise to frequency-dependent dispersion and odd-order time derivatives correspond to frequency-dependent losses. The corresponding digital simulation of an arbitrarily long (undriven and unobserved) section of medium can be simplified via commutativity to at most two pure delays and at most two linear, time-invariant filters. Every linear, time-invariant filter can be expressed as a zero-phase filter in series with an allpass filter. The zero-phase part can be interpreted as implementing a frequency-dependent gain (damping in a digital waveguide), and the allpass part can be seen as frequency-dependent delay (dispersion in a digital waveguide).
Next Section:
Alternative Wave Variables
Previous Section:
A Lossy 1D Wave Equation