DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Virtual Analog Example: Phasing

As mentioned in §5.4, the phaser, or phase shifter works by sweeping notches through a signal's short-time spectrum. The notches are classically spaced nonuniformly, while flangers employ uniformly spaced notches (§5.3). In this section, we look at using a chain of allpass filters to implement the phasing effect.

Phasing with First-Order Allpass Filters

The block diagram of a typical inexpensive phase shifter for guitar players is shown in Fig.8.23.9.20 It consists of a series chain of first-order allpass filters,9.21 each having a single time-varying parameter $ g_i(n)$ controlling the pole and zero location over time, plus a feedforward path through gain $ g$ which is a fixed depth control. Thus, the delay line of the flanger is replaced by a string of allpass filters. (A delay line is of course an allpass filter itself.)

Figure 8.23: Structure of a phaser based on four first-order allpass filters.
\includegraphics[width=4.2in]{eps/allpass1phaser}

In analog hardware, the first-order allpass transfer function [449, Appendix E, Section 8]9.22is

$\displaystyle \hbox{AP}_{1}^{\,\omega_b} \isdef \frac{s-\omega_b}{s+\omega_b}. \protect$ (9.19)

(In classic phaser circuits such as the Univibe, $ -\hbox{AP}_{1}^{\,(}\omega_b)$ is used, but since there is an even number (four) of allpass stages, there is no difference.) In discrete time, the general first-order allpass has the transfer function

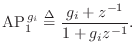
$\displaystyle \hbox{AP}_{1}^{\,g_i} \isdef \frac{g_i + z^{-1}}{1 + g_i z^{-1}}. $

We now consider the analog and digital cases, respectively.

Classic Analog Phase Shifters

Setting $ s=j\omega$ in Eq.$ \,$(8.19) gives the frequency response of the analog-phaser transfer function to be

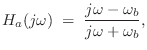
$\displaystyle H_a(j\omega) \eqsp \frac{j\omega-\omega_b}{j\omega+\omega_b}, $

where the `$ a$' subscript denotes ``analog'' as opposed to ``digital''. The phase response is readily found to be

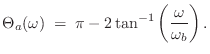
$\displaystyle \Theta_a(\omega) \eqsp \pi - 2\tan^{-1}\left(\frac{\omega}{\omega_b}\right). $

Note that the phase is always $ \pi$ at dc ($ \omega=0$), meaning each allpass section inverts at dc. Also, at $ \omega=\infty$ (remember we're talking about analog here), we get a phase of zero. In between, the phase falls from $ \pi$ to 0 as frequency goes from 0 to $ \infty$. In particular, at $ \omega=\omega_b$, the phase has fallen exactly half way, to $ \pi /2$. We will call $ \omega=\omega_b$ the break frequency of the allpass section.9.23

Figure 8.24a shows the phase responses of four first-order analog allpass filters with $ \omega_b$ set to $ 2\pi[100,200,400,800]$. Figure 8.24b shows the resulting normalized amplitude response for the phaser, for $ g=1$ (unity feedfoward gain). The amplitude response has also been normalized by dividing by 2 so that the maximum gain is 1. Since there is an even number (four) of allpass sections, the gain at dc is $ [1+(-1)(-1)(-1)(-1)]/2 = 1$. Put another way, the initial phase of each allpass section at dc is $ \pi$, so that the total allpass-chain phase at dc is $ 4\pi$. As frequency increases, the phase of the allpass chain decreases. When it comes down to $ 3\pi$, the net effect is a sign inversion by the allpass chain, and the phaser has a notch. There will be another notch when the phase falls down to $ \pi$. Thus, four first-order allpass sections give two notches. For each notch in the desired response we must add two new first-order allpass sections.

Figure 8.24: (a) Phase responses of first-order analog allpass sections with break frequencies at 100, 200, 400, and 800 Hz. (b) Corresponding phaser amplitude response.
\includegraphics[width=\twidth]{eps/phaser1a}

From Fig.8.24b, we observe that the first notch is near $ f=100$ Hz. This happens to be the frequency at which the first allpass pole ``breaks,'' i.e., $ \omega=g_1$. Since the phase of a first-order allpass section at its break frequency is $ \pi /2$, the sum of the other three sections must be approximately $ 2\pi + \pi/2$. Equivalently, since the first section has ``given up'' $ \pi /2$ radians of phase at $ \omega=g_1=2\pi100$, the other three allpass sections combined have given up $ \pi /2$ radians as well (with the second section having given up more than the other two).

In practical operation, the break frequencies must change dynamically, usually periodically at some rate.

Classic Virtual Analog Phase Shifters

To create a virtual analog phaser, following closely the design of typical analog phasers, we must translate each first-order allpass to the digital domain. Working with the transfer function, we must map from $ s$ plane to the $ z$ plane. There are several ways to accomplish this goal [362]. However, in this case, an excellent choice is the bilinear transform (see §7.3.2), defined by

$\displaystyle s \;\leftarrow\; c\frac{z-1}{z+1} \protect$ (9.20)

where $ c$ is chosen to map one particular frequency to exactly where it belongs. In this case, $ c$ can be chosen for each section to map the break frequency of the section to exactly where it belongs on the digital frequency axis. The relation between analog frequency $ \omega_a$ and digital frequency $ \omega_d$ follows immediately from Eq.$ \,$(8.20) as

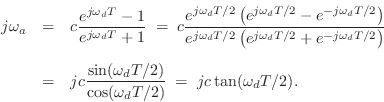
\begin{eqnarray*} j\omega_a &=& c\frac{e^{j\omega_d T}-1}{e^{j\omega_d T}+1} \eq... ...\sin(\omega_dT/2)}{\cos(\omega_dT/2)} \eqsp jc\tan(\omega_dT/2). \end{eqnarray*}

Thus, given a particular desired break-frequency $ \omega_a=\omega_d=\omega_b$, we can set

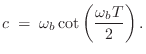
$\displaystyle c \eqsp \omega_b\cot\left(\frac{\omega_bT}{2}\right). $

Recall from Eq.$ \,$(8.19) that the transfer function of the first-order analog allpass filter is given by

$\displaystyle H_a(s) \eqsp \frac{s-\omega_b}{s+\omega_b} $

where $ \omega_b$ is the break frequency. Applying the general bilinear transformation Eq.$ \,$(8.20) gives

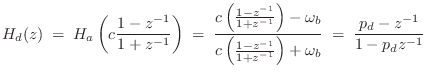
$\displaystyle H_d(z) \eqsp H_a\left(c\frac{1-z^{-1}}{1+z^{-1}}\right) \eqsp \f... ...1-z^{-1}}{1+z^{-1}}\right) + \omega_b}\\ \eqsp \frac{p_d-z^{-1}}{1-p_dz^{-1}} $

where we have denoted the pole of the digital allpass by

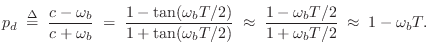
$\displaystyle p_d\isdefs \frac{c-\omega_b}{c+\omega_b} \eqsp \frac{1-\tan(\ome... ...T/2)} \;\approx\; \frac{1-\omega_bT/2}{1+\omega_bT/2} \;\approx\; 1-\omega_bT. $

Figure 8.25 shows the digital phaser response curves corresponding to the analog response curves in Fig.8.24. While the break frequencies are preserved by construction, the notches have moved slightly, although this is not visible from the plots. An overlay of the total phase of the analog and digital allpass chains is shown in Fig.8.26. We see that the phase responses of the analog and digital alpass chains diverge visibly only above 9 kHz. The analog phase response approaches zero in the limit as $ \omega_a\to\infty$, while the digital phase response reaches zero at half the sampling rate, $ 10$ kHz in this case. This is a good example of when the bilinear transform performs very well.

Figure 8.25: (a) Phase responses of first-order digital allpass sections with break frequencies at 100, 200, 400, and 800 Hz, with the sampling rate set to 20,000 Hz. (b) Corresponding phaser amplitude response.
\includegraphics[width=\twidth]{eps/phaser1d}

Figure 8.26: Phase response of four first-order allpass sections in series -- analog and digital cases overlaid.
\includegraphics[width=\twidth]{eps/phaser1ad}

In general, the bilinear transform works well to digitize feedforward analog structures in which the high-frequency warping is acceptable. When frequency warping is excessive, it can be alleviated by the use of oversampling; for example, the slight visible deviation in Fig.8.26 below 10 kHz can be largely eliminated by increasing the sampling rate by 15% or so. See the case of digitizing the Moog VCF for an example in which the presence of feedback in the analog circuit leads to a delay-free loop in the digitized system [479,477].

Phasing with 2nd-Order Allpass Filters

The allpass structure proposed in [429] provides a convenient means for generating nonuniformly spaced notches that are independently controllable to a high degree. An advantage of the allpass approach even in the case of uniformly spaced notches (which we call flanging, as introduced in §5.3) is that no interpolating delay line is needed.

Figure 8.27: Structure of a phaser based on four second-order allpass filters.
\includegraphics[width=4.2in]{eps/allpassphaser}

The architecture of the phaser based on second-order allpasses is shown in Fig.8.27. It is identical to that in Fig.8.23 with each first-order allpass being replaced by a second-order allpass. I.e., replace $ \hbox{AP}_{1}^{\,g_i}$ in Fig.8.23 by $ \hbox{AP}_{2}^{\,g_i}$, for $ i=1,2,3,4$, to get Fig.8.27. The phaser will have a notch wherever the phase of the allpass chain is at $ \pi$ (180 degrees). It can be shown that these frequencies occur very close to the resonant frequencies of the allpass chain [429]. It is therefore convenient to use a single conjugate pole pair in each allpass section, i.e., use second-order allpass sections of the form

$\displaystyle H(z) \eqsp \frac{a_2 + a_1 z^{-1} + z^{-2}}{1 + a_1 z^{-1} + a_2 z^{-2}} $

where

\begin{eqnarray*} a_1 &=& -2R\cos(\theta)\\ a_2 &=& R^2 \end{eqnarray*}

and $ R$ is the radius of each pole in the complex-conjugate pole pair, and pole angles are $ \pm\theta$. The pole angle can be interpreted as $ \theta=\omega_c T$ where $ \omega_c$ is the resonant frequency and $ T$ is the sampling interval.

Phaser Notch Parameters

To move just one notch, the tuning of the pole-pair in the corresponding section is all that needs to be changed. Note that tuning affects only one coefficient in the second-order allpass structure. (Although the coefficient $ a_1$ appears twice in the transfer function, it only needs to be used once per sample in a slightly modified direct-form implementation [449].)

The depth of the notches can be varied together by changing the gain of the feedforward path.

The bandwidth of individual notches is mostly controlled by the distance of the associated pole-pair from the unit circle. So to widen the notch associated with a particular allpass section, one may increase the ``damping'' of that section.

Finally, since the gain of the allpass string is unity (by definition of allpass filters), the gain of the entire structure is strictly bounded between 0 and 2. This property allows arbitrary notch controls to be applied without fear of the overall gain becoming ill-behaved.

Phaser Notch Distribution

As mentioned above, it is desirable to avoid exact harmonic spacing of the notches, but what is the ideal non-uniform spacing? One possibility is to space the notches according to the critical bands of hearing, since essentially this gives a uniform notch density with respect to ``place'' along the basilar membrane in the ear. There is no need to follow closely the critical-band structure, so that simple exponential spacing may be considered sufficiently perceptually uniform (corresponding to uniform spacing on a log frequency scale). Due to the immediacy of the relation between notch characteristics and the filter coefficients, the notches can easily be placed under musically meaningful control.

Next Section:
Electric Guitars
Previous Section:
Extracting Parametric Resonators from a Nonparametric Impulse Response