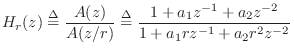Extracting Parametric Resonators from a Nonparametric Impulse Response
As mentioned in §8.7.1 above, a valuable way of shortening the excitation table in commuted synthesis is to factor the body resonator into its most-damped and least-damped modes. The most-damped modes are then commuted and combined with the excitation in impulse-response form. The least-damped modes can be left in parametric form as recursive digital filter sections.
Commuted synthesis is a technique in which the body resonator is commuted with the string model, as shown in Fig.8.10, in order to avoid having to implement a large body filter at all [439,232,229].9.18In commuted synthesis, the excitation (e.g., plucking force versus time) can be convolved with the resonator impulse response to provide a single aggregate excitation signal. This signal is short enough to store in a look-up table, and a note is played by simply summing it into the string.
Mode Extraction Techniques
The goal of resonator factoring is to identify and remove the least-damped resonant modes of the impulse response. In principle, this means ascertaining the precise resonance frequencies and bandwidths associated with each of the narrowest ``peaks'' in the resonator frequency response, and dividing them out via inverse filtering, so they can be implemented separately as resonators in series. If in addition the amplitude and phase of a resonance peak are accurately measurable in the complex frequency response, the mode can be removed by complex spectral subtraction (equivalent to subtracting the impulse-response of the resonant mode from the total impulse response); in this case, the parametric modes are implemented in a parallel bank as in [66]. However, in the parallel case, the residual impulse response is not readily commuted with the string.
In the inverse-filtering case, the factored resonator components are in cascade (series) so that the damped modes left behind may be commuted with the string and incorporated in the excitation table by convolving the residual impulse response with the desired string excitation signal. In the parallel case, the damped modes do not commute with the string since doing so would require somehow canceling them in the parallel filter sections. In principle, the string would have to be duplicated so that one instance can be driven by the residual signal with no body resonances at all, while the other is connected to the parallel resonator bank and driven only by the natural string excitation without any commuting of string and resonator. Since duplicating the string is unlikely to be cost-effective, the impulse response of the high-frequency modes can be commuted and convolved with the string excitation as in the series case to obtain qualitative results. The error in doing this is that the high-frequency modes are being multiplied by the parallel resonators rather than being added to them.
Various methods are available for estimating the mode parameters for inverse filtering:
- Amplitude response peak measurement
- Weighted digital filter design
- Linear prediction
- Sinusoidal modeling
- Late impulse-response analysis
Amplitude response peak measurement
The longest ringing modes are associated with the narrowest bandwidths. When they are important resonances in the frequency response, they also tend to be the tallest peaks in the frequency response magnitude. (If they are not the tallest near the beginning of the impulse response, they will be the tallest near the end.) Therefore, one effective technique for measuring the least-damped resonances is simply to find the precise location and width of the narrowest and tallest spectral peaks in the measured amplitude response of the resonator. The center-frequency and bandwidth of a narrow frequency-response peak determine two poles in the resonator to be factored out. Expressing a filter in terms of its poles and zeros is one type of ``parametric'' filter representation, as opposed to ``nonparametric'' representations such as the impulse response or frequency response. Prony's method [449,297,273] is one well known technique for estimating the frequencies and bandwidths of sums of exponentially decaying sinusoids (two-pole resonator impulse responses).
In the factoring example presented in §8.8.6, the frequency and bandwidth of the main Helmholtz air mode are measured manually using an interactive spectrum analysis tool. However, it is a simple matter to automate peak-finding in FFT magnitude data. (See, for example, the peak finders used in sinusoidal modeling, discussed a bit further in §8.8.1 below.)
Weighted digital filter design
Many methods for digital filter design support spectral weighting functions that can be used to focus in on the least-damped modes in the frequency response. One is the weighted equation-error method which is available in the matlab invfreqz() function (§8.6.4). Figure 8.13 illustrates use of it. For simplicity, only one frequency-response peak plus noise is shown in this synthetic example. First, the peak center-frequency is measured using a quadratically interpolating peak finder operating on the dB spectral magnitude. This is used to set the spectral weighting function. Next, invfreqz() is called to design a two-pole filter having a frequency response that approximates the measured data as closely as possible. The weighting function is also shown in Fig.8.13, renormalized to overlay on the scale of the plot. Finally, the amplitude response of the two-pole filter designed by the equation-error method is shown overlaid in the figure. Note that the agreement is quite good near the peak which is what matters most. The interpolated peak frequency measured initially in the nonparametric spectral magnitude data can be used to fine-tune the pole-angles of the designed filter, thus rendering the equation-error method a technique for measuring only the peak bandwidth in this case. There are of course many, many techniques in the signal processing literature for measuring spectral peaks.
Linear prediction
Another well known method for converting the least-damped modes into
parametric form is Linear Predictive Coding (LP) followed by polynomial
factorization to obtain resonator poles. LP is particularly good at
fitting spectral peaks due to the nature of the error criterion it minimizes
[428]. The poles closest to the unit circle in the ![]() plane can be chosen for the ``ringy'' part of the resonator. It is well
known that when using techniques like LP to model spectral peaks for
extraction, orders substantially higher than twice the number of spectral
peaks should be used. The extra degrees of freedom in the LP fit give more
poles for modeling spectral detail other than the peaks, allowing the poles
modeling the peaks to fit them with less distraction. On the other hand,
if the order chosen is too high, sometimes more than two poles will home
in on the same peak. In some cases, this may be appropriate since the
body resonances are not necessary resolvable so as to separate the peaks,
especially at high frequencies.
plane can be chosen for the ``ringy'' part of the resonator. It is well
known that when using techniques like LP to model spectral peaks for
extraction, orders substantially higher than twice the number of spectral
peaks should be used. The extra degrees of freedom in the LP fit give more
poles for modeling spectral detail other than the peaks, allowing the poles
modeling the peaks to fit them with less distraction. On the other hand,
if the order chosen is too high, sometimes more than two poles will home
in on the same peak. In some cases, this may be appropriate since the
body resonances are not necessary resolvable so as to separate the peaks,
especially at high frequencies.
Sinusoidal modeling
Another way to find the least-damped mode parameters is by means of an intermediate sinusoidal model of the body impulse response, or, more appropriately, the energy decay relief (EDR) computed from the body impulse response (see §3.2.2). Such sinusoidal models have been used to determine the string loop filter in digital waveguide strings models. In the case of string loop-filter estimation, the sinusoidal model is applied to the impulse response (or ``pluck'' response) of a vibrating string or acoustic tube. In the present application, it is ideally applied to the EDR of the body impulse response (or ``hammer-strike'' response).
Since sinusoidal modeling software (e.g. [424]) typically quadratically interpolates the peak frequencies, the resonance frequencies are generally quite accurately estimated provided the frame size is chosen large enough to span many cycles of the underlying resonance.
The sinusoidal amplitude envelopes yield a particularly robust measurement of resonance bandwidth. Theoretically, the modal decay should be exponential. Therefore, on a dB scale, the amplitude envelope should decay linearly. Linear regression can be used to fit a straight line to the measured log-amplitude envelope of the impulse response of each long-ringing mode. Note that even when amplitude modulation is present due to modal couplings, the ripples tend to average out in the regression and have little effect on the slope measurement. This robustness can be enhanced by starting and ending the linear regression on local maxima in the amplitude envelope. A method for estimating modal decay parameters in the presence of noise is given in [125,234,235].
Below is a section of matlab code which performs linear regression:
function [slope,offset] = fitline(x,y);
%FITLINE fit line 'y = slope * x + offset'
% to column vectors x and y.
phi = [x, ones(length(x),1)];
p = phi' * y;
r = phi' * phi;
t = r\p;
slope = t(1);
offset = t(2);
Late impulse-response analysis
All methods useable with inverse filtering can be modified based on the observation that late in the impulse response, the damped modes have died away, and the least-damped modes dominate. Therefore, by discarding initial impulse-response data, the problem in some sense becomes ``easier'' at the price of working closer to the noise floor. This technique is most appropriate in conjunction with the inverse filtering method for mode extraction (discussed below), since for subtraction, the modal impulse response must be extrapolated back to the beginning of the data record. However, methods used to compute the filter numerator in variations on Prony's method can be used to scale and phase-align a mode for subtraction [428,297].
One simple approximate technique based on looking only at the late impulse response is to take a zero-padded FFT of the latest Hanning-windowed data segment. The least-damped modes should give very clearly dominant peaks in the FFT magnitude data. As discussed above, the peak(s) can be interpolated to estimate the mode resonance frequency, and the bandwidth can be measured to determine the time-constant of decay. Alternatively, the time-constant of decay can be measured in the time domain by measuring the decay slope of the log amplitude envelope across the segment (this time using a rectangular window). Since the least-damped mode is assumed to be isolated in the late decay, it is easy to form a pitch-synchronous amplitude envelope.
Inverse Filtering
Whatever poles are chosen for the least-damped part, and however they are computed (provided they are stable), the damped part can be computed from the full impulse response and parametric part using inverse filtering, as illustrated in the computed examples above. The inverse filter is formed from zeros equal to the estimated resonant poles. When the inverse filter is applied to the full resonator impulse, a ``residual'' signal is formed which is defined as the impulse response of the leftover, more damped modes. The residual is in exactly the nonparametric form needed for commuting with the string and convolving with the string excitation signal, such as a ``pluck'' signal. Feeding the residual signal to the parametric resonator gives the original resonator impulse response to an extremely high degree of accuracy. The error is due only to numerical round-off error during the inverse and forward filtering computations. In particular, the least-damped resonances need not be accurately estimated for this to hold. When there is parametric estimation error, the least-damped components will fail to be completely removed from the residual signal; however, the residual signal through the parametric resonator will always give an exact reconstruction of the original body impulse response, to within roundoff error. This is similar to the well known feature of linear predictive coding that feeding the prediction error signal to the LP model always gives back the original signal [297].
The parametric resonator need not be restricted to all-pole filters, however, although all-pole filters (plus perhaps zeros set manually to the same angles but contracted radii) turn out to be very convenient and simple to work with. Many filter design techniques exist which can produce a parametric part having any prescribed number of poles and zeros, and weighting functions can be used to ``steer'' the methods toward the least-damped components of the impulse response. The equation-error method illustrated in Fig. 8.13 is an example of a method which can also compute zeros in the parametric part as well as poles. However, for inverse filtering to be an option, the zeros must be constrained to be minimum phase so that their inverses will be stable poles.
Empirical Notes on Inverse Filtering
In experiments factoring guitar body impulse responses, it was found that the largest benefit per section comes from pulling out the main Helmholtz air resonance. Doing just this shortens the impulse response (excitation table) by a very large factor, and because the remaining impulse response is noise-like, it can be truncated more aggressively without introducing artifacts.
It also appears that the bandwidth estimate is not very critical in this case. If it is too large, or if ``isolation zeros'' are not installed behind the poles, as shown in Figs. 8.18b and 8.21b, the inverse filtering serves partially as a preemphasis which tends to flatten the guitar body frequency response overall or cause it to rise with frequency. This has a good effect on the signal-to-quantization-noise ratio versus frequency. To maximize the worst-case signal-to-quantization-noise versus frequency, the residual spectrum should be flat since the quantization noise spectrum is normally close to flat. A preemphasis filter for flattening the overall spectrum is commonly used in speech analysis [363,297]. A better preemphasis in this context is an inverse equal-loudness preemphasis, taking the inverse of an equal-loudness contour near the threshold of hearing in the Fletcher-Munson curves [475]. This corresponds to psychoacoustic ``noise shaping'' so that the quantization noise floor is perceptually uniform, and decreasing playback volume until it falls below the threshold of hearing results in all of the noise disappearing across the entire spectrum at the same volume.9.19
Since in some fixed-point implementations, narrow bandwidths may be
difficult to achieve, good results are obtained by simply setting the
bandwidth of the single resonator to any minimum robust value. As a
result, there may still be some main-air-mode response in the residual
signal, but it is typically very small, and early termination of it using a
half-window for table shortening is much less audible than if the original
impulse response were similarly half-windowed. The net effect on the
instrument is to introduce artificial damping the main air mode in
the guitar body. However, since this mode rings so much longer than the
rest of the modes in the guitar body, shortening it does not appear to be
detrimental to the overall quality of the instrument. In general, it is
not desirable for isolated modes to ring longer than all others. Why would
a classical guitarist want an audible ``ringing'' of the guitar body near
![]() Hz?
Hz?
In computing figures 8.16 and
Fig. 8.16b, the estimated ![]() of the main
Helmholtz air mode was only
of the main
Helmholtz air mode was only ![]() . As a result, it is still weakly present
in the inverse filter output (residual) spectrum
Fig. 8.16b.
. As a result, it is still weakly present
in the inverse filter output (residual) spectrum
Fig. 8.16b.
Matlab Code for Inverse Filtering
Below is the matlab source code used to extract the main Helmholtz air mode from the guitar body impulse response in Figures 8.14 through 8.17:
freq = 104.98; % estimated peak frequency in Hz
bw = 10; % peak bandwidth estimate in Hz
R = exp( - pi * bw / fs); % pole radius
z = R * exp(j * 2 * pi * freq / fs); % pole itself
B = [1, -(z + conj(z)), z * conj(z)] % numerator
r = 0.9; % zero/pole factor (notch isolation)
A = B .* (r .^ [0 : length(B)-1]); % denominator
residual = filter(B,A,bodyIR); % apply inverse filter
Sinusoidal Modeling of Mode Decays
When the amplitude envelope, frequency, phase, and onset time are all accurately estimated (for all time), it is possible to subtract the synthesized modal impulse response from the measured impulse response. (This contrasts with purely spectral modal parameters which are amplitude, frequency, bandwidth, and phase.) This method of ``sinusoidal track removal'' is used in sines-plus-noise spectral modeling. (See [424] for further details and supporting C software). In this approach, the resonant mode is subtracted out rather than divided out of the frequency response.
There are some disadvantages of subtraction relative to inverse filtering. First, more parameters must be accurately measured; the precise gain and phase of the resonance are needed in addition to its frequency and bandwidth. Inverse filtering on the other hand requires only estimation of frequency and bandwidth (or frequency and time-constant of decay). In addition, the residual impulse response after subtraction cannot be precisely commuted with the string for commuted synthesis.
The advantages of subtraction over inverse filtering are that amplitude modulation due to mode coupling can be retained in the measured modal decay and subtracted out, whereas a second-order inverse filter cannot subtract out the modulation due to coupling. Also, if the system is time varying (as happens, for example, when the performer's hand is pressing against the resonating body in a time-varying way), the subtraction method can potentially track the changing modal parameters and still successfully remove the modal decay. To compete with this, the inverse filtering method would have to support a time-varying filter model. As another example, if the guitar body is moving, the measured response is a time-varying linear combination of fixed resonant modes (although some Doppler shift is possible). The subtraction method can follow a time-varying gain (and phase) so that the subtraction still will take out the mode.
The inverse filtering method seems most natural when the physical resonator is time-invariant and is well modeled as a series of resonant sections. It is also the only one strictly valid for use in commuted synthesis. The subtraction method seems most natural when the physical resonator is best modeled as a sum of resonating modes. As a compromise between the two approaches, all parametric modes may be separated from the nonparametric modes by means of inverse filtering, and the parametric part can then be split into parallel form.
Parallel Body Filterbank Design
In [66], a method is described for producing a parallel bank of fourth-order IIR body filters from an arbitrary starting impulse response. Initially, the body impulse is approximated by the impulse response of a fourth-order IIR filter using an algorithm of second author Cheng; the method is said to pick out the most resonant modes of the sampled impulse response, and fourth-order sections were found experimentally to best characterize the resonant modes of the guitar body. The impulse response of the filter so designed is subtracted from the measured impulse response to form a residual impulse response which is given again to the IIR design algorithm. This process is repeated to obtain a parallel bank of fourth-order filters, plus a final residual which is discarded. In the present context, the final residual should be incorporated at least qualitatively into the string excitation signal, or else the method should be applied only to the total parametric impulse response computed by other means and separated from the nonparametric impulse response by inverse filtering.
Approximating Shortened Excitations as Noise
Figure 8.14b suggests that the many
damped modes remaining in the shortened body impulse response may not
be clearly audible as resonances since their decay time is so short.
This is confirmed by listening to shortened and spectrally flattened
body responses which sound somewhere between a click and a noise
burst. These observations suggest that the shortened, flattened, body
response can be replaced by a psychoacoustically equivalent
noise burst, as suggested for modeling piano soundboards
[519]. Thus, the signal of
Fig. 8.14b can be synthesized
qualitatively by a white noise generator multiplied by an amplitude
envelope. In this technique, it is helpful to use LP on the residual
signal to flatten it. As a refinement, the noise burst can be
time-varying filtered so that high frequencies decay faster
[519]. Thus, the stringed instrument model may consist of
noise generator
![]() excitation amplitude-shaping
excitation amplitude-shaping
![]() time-varying lowpass
time-varying lowpass
![]() string model
string model
![]() parametric resonators
parametric resonators
![]() multiple outputs.
In addition, properties of the physical excitation may be
incorporated, such as comb filtering to obtain a virtual pick or
hammer position. Multiple outputs
provide for individual handling of the most important resonant modes
and facilitate simulation of directional radiation characteristics
[511].
multiple outputs.
In addition, properties of the physical excitation may be
incorporated, such as comb filtering to obtain a virtual pick or
hammer position. Multiple outputs
provide for individual handling of the most important resonant modes
and facilitate simulation of directional radiation characteristics
[511].
It is interesting to note that by using what is ultimately a noise-burst excitation, we have almost come full circle back to the original extended Karplus-Strong algorithm [236,207]. Differences include (1) the amplitude shaping of the excitation noise to follow the envelope of the impulse-response of the highly damped modes of the guitar body (convolved with the physical string excitation), (2) more sophisticated noise filtering which effectively shapes the noise in the frequency domain to follow the frequency response of the highly damped body modes (times the excitation spectrum), and (3) the use of factored-out body resonances which give real resonances such as the main Helmholtz air mode. The present analysis also provides a theoretical explanation as to why use of a noise burst in the Karplus-Strong algorithm is generally considered preferable to a theoretically motivated initial string shape such as the asymmetric triangular wave which leans to the left according to pick position [437, p. 82].
From a psychoacoustical perspective, it may be argued that the excitation noise burst described above is not perceptually uniform. The amplitude envelope for the noise burst provides noise-shaping in the time domain, and the LP filter provides noise-shaping in the frequency domain, but only at uniform resolution in time and frequency. Due to properties of hearing, it can be argued that multi-resolution noise shaping should be used. Thus, the LP fit for obtaining the noise-shaping filter should be carried out over a Bark frequency axis as in Fig. 8.19b. Since LP operates on the autocorrelation function, a warped autocorrelation can be computed simply as the inverse FFT of the warped squared-magnitude spectrum.
Body Factoring Example
![\includegraphics[width=3.5in]{eps/fbrBodyIRandShortenedmatti}](http://www.dsprelated.com/josimages_new/pasp/img1874.png) |
Figure 8.14a shows the impulse
response of a classical guitar body sampled at ![]() kHz. It was
determined empirically that at least the first
kHz. It was
determined empirically that at least the first ![]() msec of this
impulse response needs to be stored in the excitation table to produce
a high quality synthetic guitar. Figure
8.14b shows the same impulse response
after factoring out a single resonating mode near
msec of this
impulse response needs to be stored in the excitation table to produce
a high quality synthetic guitar. Figure
8.14b shows the same impulse response
after factoring out a single resonating mode near ![]() Hz (the main
Helmholtz air mode). A close-up of the initial response is shown in
Fig. 8.15. As can be seen, the
residual response is considerably shorter than the original.
Hz (the main
Helmholtz air mode). A close-up of the initial response is shown in
Fig. 8.15. As can be seen, the
residual response is considerably shorter than the original.
![\includegraphics[width=3.5in]{eps/fbrBodyFRandShortenedmatti}](http://www.dsprelated.com/josimages_new/pasp/img1877.png) |
Figure 8.16a shows the guitar-body amplitude response, and Fig. 8.16b shows the response after the main Helmholtz air mode is removed by inverse filtering with a two-pole, two-zero filter. Figure 8.18 shows the same thing but with only a two-zero inverse filter; in this case the overall spectral shape is more affected.
![\includegraphics[width=3.5in]{eps/fbrBodyFRandShortenedmattiRat0}](http://www.dsprelated.com/josimages_new/pasp/img1879.png) |
![\includegraphics[width=3.5in]{eps/fbrBodyFRandShortenedmattiw}](http://www.dsprelated.com/josimages_new/pasp/img1880.png) |
![\includegraphics[width=3.5in]{eps/fbrBodyFRandShortenedmattiwRat0}](http://www.dsprelated.com/josimages_new/pasp/img1882.png) |
Figure 8.19a shows the measured guitar-body amplitude response after warping to an approximate Bark frequency axis. Figure 8.19b shows the Bark-warped amplitude response after the main Helmholtz air mode is removed by inverse filtering. Fig. 8.20 shows the low-frequency close-up. The warped amplitude response was computed as the FFT of the impulse response of the FIR filter given by the original impulse response with each unit delay being replaced by a first-order allpass filter, as originally suggested in [334] and described further in [229].
Fig. 8.21 shows the corresponding
results if a two-zero inverse filter is used rather than a two-pole,
two-zero inverse filter, i.e., without the ``isolation poles,'' (![]() in Eq.
in Eq.![]() (8.18) below). In this case, there is an overall ``EQ''
boosting high frequencies and attenuating low frequencies. However,
comparing Figs. 8.18b and
8.21b, we see that the global EQ
effect is less pronounced in the Bark-warped case. On the Bark
frequency scale, it is much easier numerically to eliminate the main
air mode.
(8.18) below). In this case, there is an overall ``EQ''
boosting high frequencies and attenuating low frequencies. However,
comparing Figs. 8.18b and
8.21b, we see that the global EQ
effect is less pronounced in the Bark-warped case. On the Bark
frequency scale, it is much easier numerically to eliminate the main
air mode.
The modal bandwidth used in the inverse filtering was chosen to be
![]() Hz which corresponds to a
Hz which corresponds to a ![]() of
of ![]() for the main air mode. If
the Bark-warping is done using a first-order conformal map
[458], its inverse preserves filter order
[428, pp. 61-67]. Applying the inverse warping to the
parametric resonator drives its pole radius from
for the main air mode. If
the Bark-warping is done using a first-order conformal map
[458], its inverse preserves filter order
[428, pp. 61-67]. Applying the inverse warping to the
parametric resonator drives its pole radius from ![]() in the
Bark-warped
in the
Bark-warped ![]() plane to
plane to ![]() in the unwarped
in the unwarped ![]() plane.
plane.
Note that if the inverse filter consists only of two zeros determined by the spectral peak parameters, other portions of the spectrum will be modified by the inverse filtering, especially at the next higher resonance, and in the linear trend of the overall spectral shape. To obtain a more localized mode extraction (useful when the procedure is to be repeated), we define the inverse filter as
where
Because the main air mode is extremely narrow, the probability of overflow
can be reduced in fixed-point implementations by artificially dampening it.
Reducing the ![]() of the main Helmholtz air mode from
of the main Helmholtz air mode from ![]() to
to ![]() corresponds to a decay time of about
corresponds to a decay time of about
![]() sec.
This is consistent with the original desire to retain the first
sec.
This is consistent with the original desire to retain the first ![]() msec
of the body impulse response.
msec
of the body impulse response.
![\includegraphics[width=\twidth]{eps/fbrBodyIRandShortenedmattiw}](http://www.dsprelated.com/josimages_new/pasp/img1889.png) |
For completeness, the Bark-warped impulse-responses are also shown in Figs. 8.22. Figure 8.22a shows the complete Bark-warped impulse response obtained by taking the inverse FFT of Fig. 8.19a, and Fig. 8.22b shows the shortened Bark-warped impulse response defined as the inverse FFT of Fig. 8.19b. We see that given a Bark-warped frequency axis (which more accurately represents what we hear), the time duration of the high-frequency modes is extended while the low-frequency modes are contracted in time duration. Thus, the modal decay times show less of a spread versus frequency. This also accounts for the reduced apparent shortening by the inverse filtering in the Bark-warped case.
Next Section:
Virtual Analog Example: Phasing
Previous Section:
Commuted Synthesis








![\includegraphics[width=0.8\twidth]{eps/fbrUsingInvfreqz}](http://www.dsprelated.com/josimages_new/pasp/img1872.png)
![\includegraphics[width=3.5in]{eps/fbrZoomedBodyIRandShortenedmatti}](http://www.dsprelated.com/josimages_new/pasp/img1875.png)
![\includegraphics[width=3.5in]{eps/fbrZoomedBodyFRandShortenedmatti}](http://www.dsprelated.com/josimages_new/pasp/img1878.png)
![\includegraphics[width=3.5in]{eps/fbrZoomedBodyFRandShortenedmattiw}](http://www.dsprelated.com/josimages_new/pasp/img1881.png)