DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Correlation Analysis

Correlation analysis applies only to stationary stochastic processes (§C.1.5).

Cross-Correlation


Definition: The cross-correlation of two signals $ x$ and $ y$ may be defined by

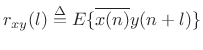$\displaystyle r_{xy}(l) \isdef E\{\overline{x(n)}y(n+l)\}$ (C.24)

I.e., it is the expected value (§C.1.6) of the lagged products in random signals $ x$ and $ y$ .

Cross-Power Spectral Density

The DTFT of the cross-correlation is called the cross-power spectral density, or ``cross-spectral density,'' ``cross-power spectrum,'' or even simply ``cross-spectrum.''

Autocorrelation

The cross-correlation of a signal with itself gives the autocorrelation function of that signal:

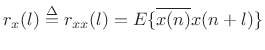$\displaystyle r_{x}(l) \isdef r_{xx}(l) = E\{\overline{x(n)}x(n+l)\}$ (C.25)

Note that the autocorrelation function is Hermitian:

$\displaystyle r_x(-l) = \overline{r_x(l)} $

When $ x$ is real, its autocorrelation is symmetric. More specifically, it is real and even.

Sample Autocorrelation

See §6.4.

Power Spectral Density

The Fourier transform of the autocorrelation function $ r_x(l)$ is called the power spectral density (PSD), or power spectrum, and may be denoted

$\displaystyle S_x(\omega) \isdef \hbox{\sc DTFT}_\omega(r_x). $

When the signal $ x$ is real, its PSD is real and even, like its autocorrelation function.

Sample Power Spectral Density

See §6.5.

Next Section:
White Noise
Previous Section:
Random Variables & Stochastic Processes