Phase or Frequency Shifter Using a Hilbert Transformer

• Matlab
• Tutorials

In this article, we’ll describe how to use a Hilbert transformer to make a phase shifter or frequency shifter.  In either case, the input is a real signal and the output is a real signal.  We’ll use some simple Matlab code to simulate these systems.  After that, we’ll go into a little more detail on Hilbert transformer theory and design. 

Phase Shifter

A conceptual diagram of a phase shifter is shown in Figure 1, where the bold lines indicate complex signals. The input is cos(ωt+ϕ).  As we’ll discuss later in this article, the Hilbert transformer [1,2] converts this input to a complex analytic signal e^j(ωt+ϕ) = cos(ωt+ϕ) + jsin(ωt+ϕ).  We multiply this signal by e^jθ , where θ is the desired phase shift, to obtain the complex signal e^j(ωt+ϕ+θ).  The real part of this signal is our desired output: y= cos(ωt+ϕ+θ).

Writing the Hilbert complex output as I + jQ, y is then:

$$y= Re\{(I+jQ)e^{j\theta}\}$$

$$\qquad = Re\{(I+jQ)(cos\theta+jsin\theta\}$$

$$\qquad y= Icos\theta - Qsin\theta  \qquad (1) $$

This allows us to implement the phase shifter using the block diagram of Figure 2.  Note there is no “j” anywhere in Figure 2:  all signals are real!  In particular, the Q signal is a real number – in calculations we can use it to form the imaginary part of the complex signal I + jQ.  As you probably know, I stands for In-phase component and Q stands for Quadrature component.  I and Q are also frequently called x_re and x_im.

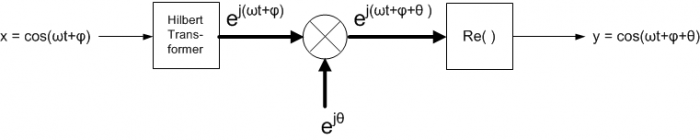
Figure 1.Phase Shifter Conceptual Diagram

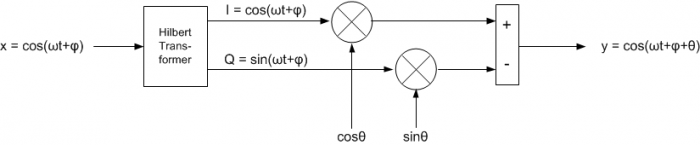
Figure 2.  Phase Shifter Implementation.

The following Matlab code implements the block diagram of Figure 2.  A 31-tap Hilbert transformer is realized as shown, where we take the theoretical coefficient values and multiply by a Hamming window to get the coefficients b1.  We also create b2, which is a simple delay of 15 samples – this represents the delay of the center tap of the Hilbert transformer’s tapped delay network.

    % 31-tap Hilbert transformer
    b= 2/pi * [-1/15 0 -1/13 0 -1/11 0 -1/9 0 -1/7 0 -1/5 0 -1/3 0 -1 0 1 0 … 
              1/3 0 1/5 0 1/7 0 1/9 0 1/11 0 1/13 0 1/15];
    b1= b.*hamming(31)';                          % window the coefficients
    b2= [0 0 0 0  0 0 0 0  0 0 0 0  0 0 0 1];     % delay of 15 (center tap of HT)

For a preview of the structure of the Hilbert transformer, see Figure 9.  Next we create sinusoidal input x with frequency 6 Hz and sample frequency of 100 Hz:

    fs= 100;                    % Hz sample frequency
    Ts= 1/fs;
    N= 128;
    n= 0:N-1;
    f0= 6;                       % Hz freq of input signal
    x= cos(2*pi*f0*n*Ts);        % input signal

Now apply input x to the Hilbert transformer.  The I output is just the center tap of the filter’s tapped delay line.

    I= filter(b2,1,x);        % I= center tap of HT
    Q= filter(b1,1,x);        % Q= output of HT

Finally, we implement equation 1 for phase shift of –π/3:

    theta= -pi/3;                          % rad phase shift with respect to I
    y= I*cos(theta) - Q*sin(theta);        % phase shifter output

Figures 1 and 2 assume no phase shift in the I-channel output of the Hilbert transformer.  However, the actual implementation has a delay of 15 samples.  This means the phase shift of –π/3 occurs with respect to the Hilbert transformer’s I output (center tap of the delay network).  Figure 3 plots 32 samples of y and I on the same graph.  As desired, y lags I by π/3 radians.

It’s worth noting that the phase shift does not depend on the frequency of the input sinusoid; as long as the frequency is within the passband of the Hilbert transformer, we get the desired phase shift.  For example, Figure 4 shows a +π/4 phase shift for input signal frequencies of 6 Hz and 9 Hz.

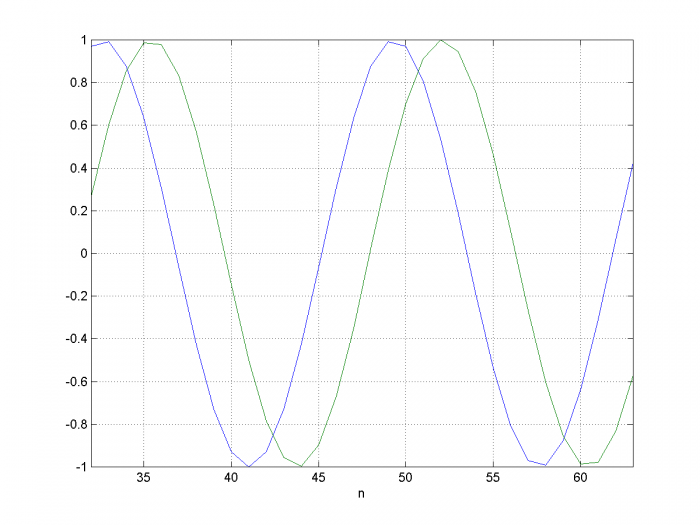
Figure 3.Phase Shifter input and output for f₀ = 6 Hz, f_s= 100 Hz, and ϕ= - π/3

Blue = Hilbert I-channel           Green=output

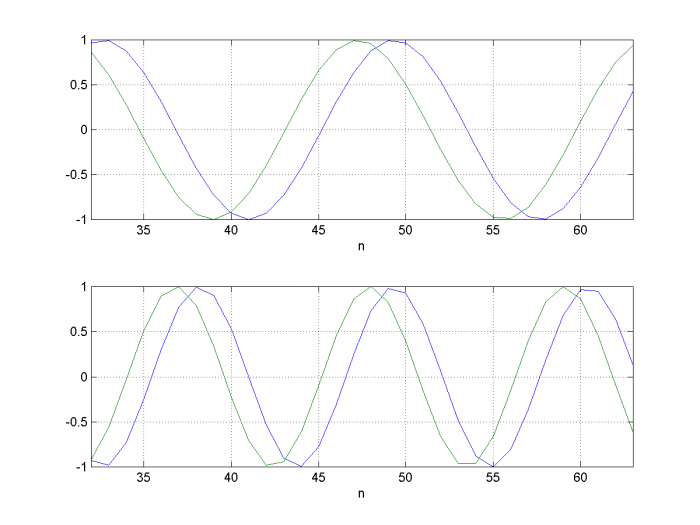
Figure 4.Phase Shifter I channel (blue) and output (green) for ϕ= + π/4, f_s= 100 Hz.

Top: f0= 6 Hz        Bottom: f0 = 9 Hz.

Frequency Shifter

The frequency shifter block diagram is shown in Figure 5.  It is the same as the phase shifter, except we let θ in Equation 1 equal dω*t, where dω (rad/s) is the desired frequency shift.  The cos(dω*t) and sin(dω*t) signals are generated by an NCO.  We assume the input x is band-limited, so that its spectrum falls within the passband of the Hilbert transformer.

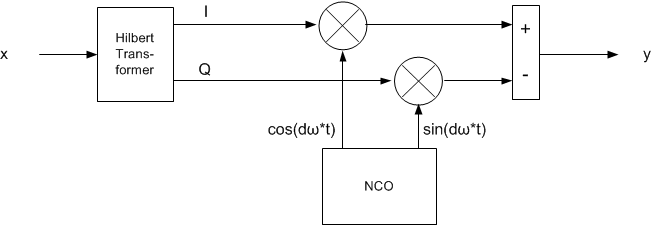
Figure 5.  Frequency Shifter Implementation.

Now we’ll develop some Matlab code to shift the frequency of an input signal centered at 12 Hz by +3 Hz.  First, we modify the Hilbert transformer used previously by replacing the Hamming window with a Blackman window.  Compared to the Hamming window, this gives a more accurate passband response, at the expense of response flatness at low frequency.  We will also quantize the coefficients to 12 bits.

    % 31-tap Hilbert transformer
    b= 2/pi * [-1/15 0 -1/13 0 -1/11 0 -1/9 0 -1/7 0 -1/5 0 -1/3 0 -1 0 1 0 … 
               1/3 0 1/5 0 1/7 0 1/9 0 1/11 0 1/13 0 1/15];
    b1= b.*blackman(31)';                         % window the coefficients
    b1= round(b1*2^12)/2^12;                      % quantize coefficients
    b2= [0 0 0 0  0 0 0 0  0 0 0 0  0 0 0 1];     % delay of 15 (center tap of HT)

Now we’ll generate the input signal x and apply it to the Hilbert transformer.  Rather than using a sinusoid, we’ll use a modulated pulse with approximately rectangular spectrum.  The Matlab function to generate the pulse is listed in the Appendix.

fs= 100;                       % Hz sample frequency
Ts= 1/fs;
N= 2048;
n= 0:N-1;
fc= 12;                        % Hz carrier frequency
bw= 2;                         % Hz -3 dB bandwidth of modulated pulse
x= .5*modpulse(fc,bw,N,fs);    % modulated pulse with approx rect spectrum
% Apply modulated pulse to Hilbert transformer
I= filter(b2,1,x);             % I= center tap of HT filter
Q= filter(b1,1,x);             % Q= output of HT filter

Next we generate the NCO output and use it to shift the frequency.  The modulus function is used to make the NCO’s phase accumulator roll-over when its value exceeds 1.

    df= 3;                              % Hz desired frequency shift
    u= mod(df*n*Ts,1);                  % phase accumulator
    theta= 2*pi*u;                      % phase
    y= I.*cos(theta) –Q.*sin(theta);    % final output

At this point, we can find the spectrum of the real output y.  However, it’s instructive to look at the spectra of all of the signals in Figure 5.  We have the real signals x and y, plus three complex quantities:  the Hilbert transformer output; the NCO output; and the complex product of the NCO and Hilbert outputs.  The complex quantities are easily calculated as follows:

    xc= I + j*Q;            % complex Hilbert transformer output
    nco= exp(j*theta);      % complex nco output
    yc= xc.*nco;            % complex product

We compute the spectrum of each quantity as follows:

    X= fft(x,N);          XdB= 20*log10(abs(x));
    XC= fft(xc,N);        XCdB= 20*log10(abs(XC));
    YC= fft(yc,N);        YCdB= 20*log10(abs(YC));
    NCO= psd(nco,N,fs);   NCOdB= 10*log10(abs(NCO));
    Y= fft(y,N);          YdB= 20*log10(abs(Y));

These spectra are shown in Figure 6, where we have shifted the portion of the spectrum above f_s/2 to the range –f_s/2 to 0.  Figure 6a shows the spectrum of real input signal x, and Figure 6b shows that of the complex Hilbert output xc, which approximates an analytic signal.  That is, it has negligible frequency components for f < 0.  Figure 6c shows the spectrum of NCO signal exp(jθ), which is also analytic, having a single component at +3 Hz.  Figure 6d shows the spectrum of the complex product.  As you can see, the complex multiplication has shifted the center of xc from 12 Hz to 15 Hz.  Finally, Figure 6e shows the spectrum of the real output y, centered at 15 Hz.

Had we multiplied two real signals instead of complex signals, we would have gotten duplicate spectra centered at 9 and 15 Hz:  not a useful result.  This shows the power of using complex signals.  Finally, note that we didn’t need to know the frequency of the input signal – the frequency shifter works on any signal in the Hilbert transformer’s passband.

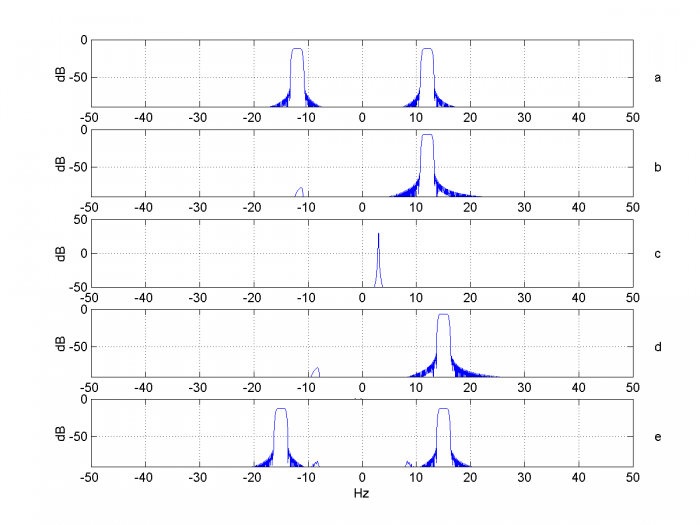
Figure 6. Spectra of signals within the frequency shifter.

a. real input X    b. Hilbert output XC    c. NCO output, df= 3 Hz

d. complex product YC     e. Final output Y

Now let’s examine the purity of the output spectrum.  The spectra of the real input signal x and real output signal y are plotted in Figure 7.  The sideband at 9 Hz is caused by the Hilbert Transformer not having perfect response magnitude of 1.  This is due to the truncation of coefficients to 31 taps and quantization of the coefficients.

While we’re looking at imperfections, we can also quantize the NCO phase and NCO output (LUT quantization).  The following code quantizes these to 10 bits.  The resulting output spectrum is shown in Figure 8.

    u= mod(df*n*Ts,1);                        % phase accumulator
    u= round(u*2^10)/2^10;                    % phase quantization
    theta= 2*pi*u;                            % quantized phase
    costheta= round(2^10*cos(theta))/2^10;    % NCO output quantization
    sintheta= round(2^10*sin(theta))/2^10;
    y= I.*costheta -Q.*sintheta;

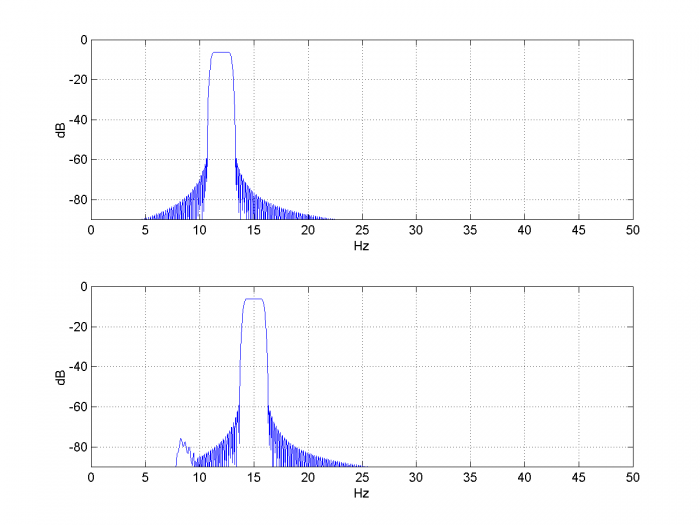
Figure 7.Spectra of frequency shifter input and output for fc= 12 Hz, df= 3 Hz,

HT length= 31 taps, HT quantization= 12 bits, fs= 100 Hz.

[h,f]= freqz(y,1,N,fs);   H= 20*log10(abs(h));

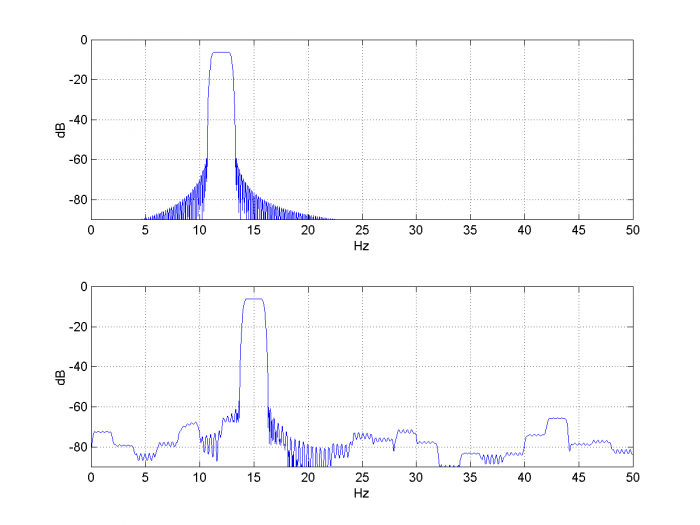
Figure 8.Spectra of frequency shifter input and output for fc= 12 Hz, df= 3 Hz,

HT length= 31 taps, HT quantization= 12 bits, fs= 100 Hz,

NCO phase quantization = 10bits, NCO LUT quantization= 10 bits.

Hilbert Transformer

Here we’ll touch on the math behind the Hilbert transformer, and we’ll look at basics of how to implement one.  A more detailed description of the theory of the Hilbert transformer is presented in references [1,2].

An ideal discrete Hilbert transformer Q-channel output has frequency response:

$$H(z)= -j, \qquad 0\lt f \lt f_s/2$$

$$\qquad \qquad \qquad= j,\qquad -f_s/2 \lt f \lt 0 \qquad (2) $$

This response can only be approximated by a practical filter (skip ahead to Figure 11 for an example).  The impulse response over -∞ < n < ∞ is:

$$h[n]=\frac{2}{\pi n},\qquad for\, n\, odd$$

$$\qquad \qquad \quad = 0,\qquad for\, n\, even \qquad (3)$$

This impulse response is non-causal, but it can be approximated by truncating, letting n =

–N/2 : N/2-1, where N is even and N+1 is the number of taps.  The taps can then be multiplied by a window function.  A block diagram of a 7-tap Hilbert Transformer is shown in Figure 9 [3], where the top diagram numbers the taps according to Equation 3, and the bottom diagram renumbers them to start with b₀.  The I-channel is taken as the center tap of the delay network, which corresponds to t = 0 in the ideal Hilbert transformer.

The Q-channel response of–j = e^-jπ/2 gives a π/2 phase lag for a sinusoidal input.  Thus, for I = cos(ωt), Q is sin(ωt).  We can then define the complex signal I + jQ = cos(ωt) +jsin(ωt) = e^jωt.  Unlike the real input signal, this signal has no spectral component at -ω.  Signals with no spectral components for f < 0 are called analytic signals.

In general, the output of the Hilbert transformer is analytic for input signals in its passband .  For example, in the preceding section, the modulated pulse signal was transformed into an (approximately) analytic signal, with spectrum shown in Figure 6b.

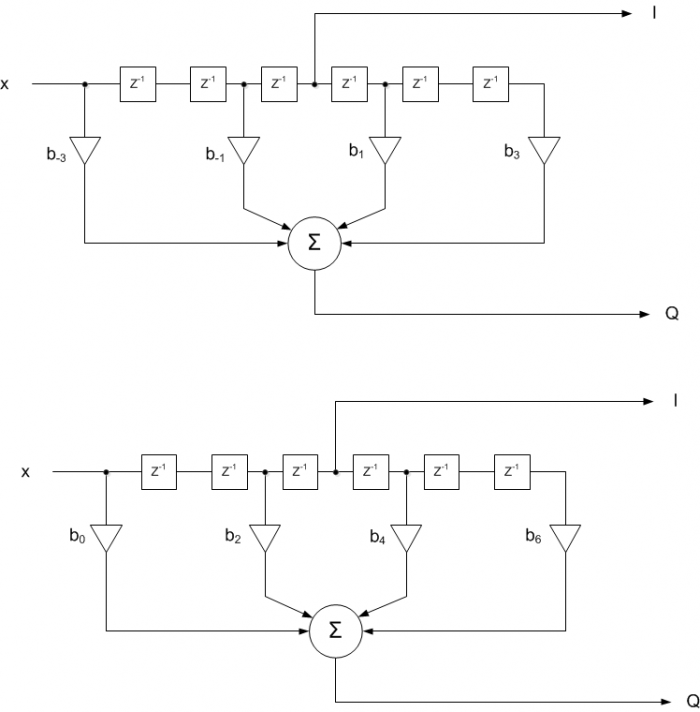
Figure 9.  7-tap Hilbert Transformer.  Top:  with taps numbered per Equation 3.

Bottom:  with taps re-numbered to start with b₀.

In the previous section, we implemented a 31-tap Hilbert transformer by windowing the truncated coefficients of Equation 3 with a Blackman window.  Here is the code again:

     % 31-tap Hilbert transformer
    b= 2/pi * [-1/15 0 -1/13 0 -1/11 0 -1/9 0 -1/7 0 -1/5 0 -1/3 0 -1 0 1 0 … 
               1/3 0 1/5 0 1/7 0 1/9 0 1/11 0 1/13 0 1/15];
    b1= b.*blackman(31)';                         % window the coefficients
    b1= round(b1*2^12)/2^12;                      % quantize coefficients
    b2= [0 0 0 0  0 0 0 0  0 0 0 0  0 0 0 1];     % delay of 15 (center tap of HT)

These coefficients are plotted in Figure 10.  Now let’s compute frequency response.  In making a realizable filter, we delayed the input by 15 samples to create the I channel.  Thus we need to calculate the response with respect to this delayed version of the input.  The Matlab code is listed below and the response is plotted in Figure 11.  As you can see, the response is pure imaginary and deviates from Equation 2 at low frequencies and near f_s/2.  When using the Hilbert transformer, we need to make sure that the signal frequency is in the flat part of the response.

    N= 1024;
    k= -N/2:N/2-1;
    f= k*fs/N;
    h_Q= fft(b1,N);            % h_Q = response of b1
    h_I= fft(b2,N);            % h_I = response at center tap (delay of 15 samples)
    h= h_Q./h_I;
    h= fftshift(h);            %shift dc to center (swap left and right halves of h)
    plot(f,imag(h))

Finally, regarding this window method of Hilbert transformer design:  while straightforward, it is typically not the most efficient method.  An efficient approach uses the Parks-McClellan equiripple FIR design algorithm, which is implemented by the Matlab function firpm [4].  This function has a mode specifically for Hilbert transformer design.

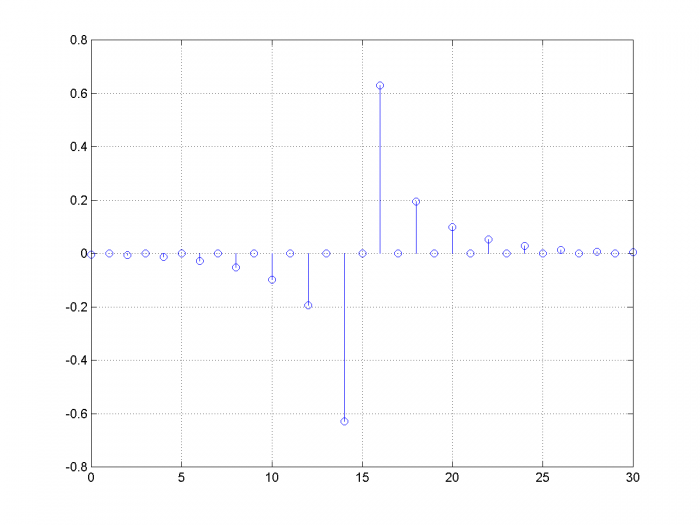
Figure 10.  Coefficients of 31-tap Hilbert Transformer.

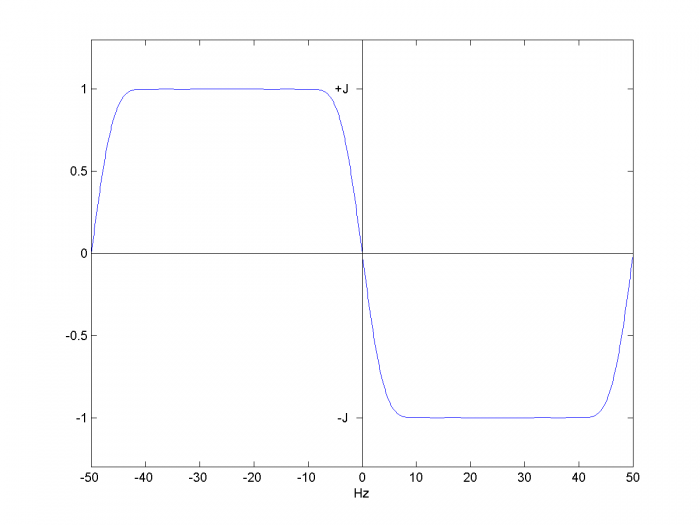
Figure 11.  Frequency Response of 31-tap Hilbert transformer, f_s= 100 Hz

 (Blackman window)

References

1.  Mitra, Sanjit K., Digital Signal Processing, 2^nd Ed., McGraw-Hill, 2001, section 11.7.

2.  Lyons, Richard G., Understanding Digital Signal Processing, 2^nd Ed., Pearson, 2004, Ch. 9.

3.  Lyons, p 374.

4.  Mathworks website, https://www.mathworks.com/help/signal/ref/firpm.html

March, 2018   Neil Robertson

Appendix    Matlab Function to Generate a Modulated Pulse

This function generates a modulated pulse having an approximately rectangular spectrum.  The pulse envelope response is generated using a window-based FIR lowpass filter.  An example pulse output is shown in Figure A.1, and its spectrum is shown in Figure A.2.

%function y = modpulse(fc,bw,N,fs)  3/10/18 Neil Robertson
%
% Modulated pulse with approximately rectangular spectrum
% fc = carrier freq, Hz
% bw = -3 dB bw of modulated pulse spectrum, Hz
% N = pulse length including padding, samples.N must be a multiple of 8.
% fs = sample frequency, Hz
%
% example:y= modpulse(20,4,1024,100)
%
function y = modpulse(fc,bw,N,fs)
if mod(N,8)~=0
    error('N must be a multiple of 8')
end
M= N/4;                        % FIR filter number of taps
Ts= 1/fs;
n= 0:N-1;
f1= bw/2;
win= kaiser(M,5);
b= fir1(M-1,2*f1/fs,win);        % window-based FIR coeffs, M taps
pad= zeros(1,(N-M)/2);
d= [pad b pad];                  % padded pulse with total length = N
x= cos(2*pi*fc*n*Ts);            % carrier
y= x.*d;                         % modulated pulse

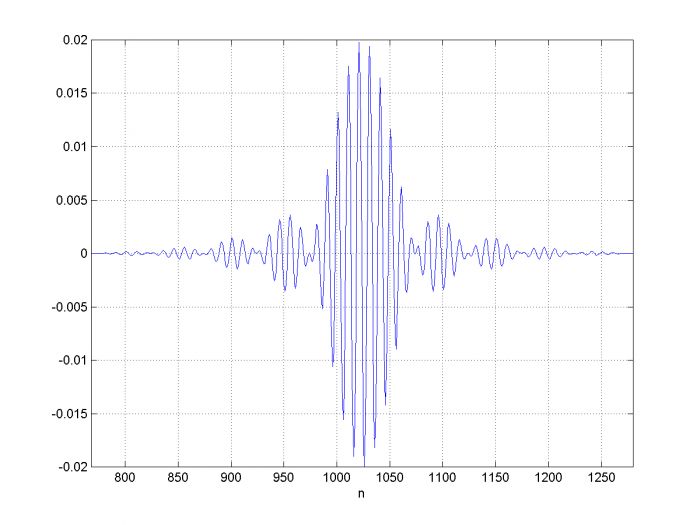
Figure A.1  512 samples of modulated pulse y= modpulse(fc,bw,N,fs)

fc= 10, bw= 2, N= 2048, fs= 100.

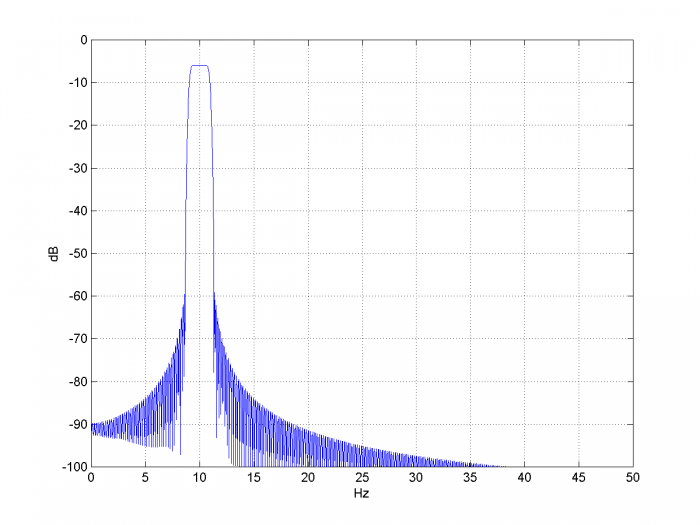
Figure A.2  Spectrum of modulated pulse.

Sign in