Hi all,
I got an FPGA design running #FFT at 256 points. Our system requires fft be configured as either 256 or 512 points on the run. I can use variable fft that can be adjusted to either 256 or 512 but the design would be much easier and possibly resource efficient if I use 256 resolution only even for 512 case.
The question then is it possible to combine two fft 256 points in some way to get equivalent 512 points.
Regards
Kaz

Hello Kaz,
Yes, there's a way to compute a 512-point FFT (on real-valued input samples) using a standard complex-valued 256-point FFT software algorithm. I cover that technique in Chapter 13 ("DSP Tricks" chapter) of my DSP book. That technique looks like the following:
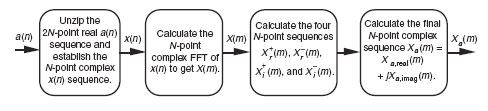
If this technique is of interest to you, just send me a private e-mail, at: R dot Lyons at ieee dot org, and I'll send the technique's details to you. (I didn't invent this "FFT trick". I wish I had. It was invented many decades ago by the pioneers of DSP.)

Thanks Rick,
Just to make sure you are aware of my setup.I use FPGA platform(not software) and use Altera's fft ip core set to 256 points on complex input and get 256 points complex fft output. I have no intention to go under the "fft bonnet" to modify its internal computations. What I want is that given two fft 256 complex outputs from the ip core I then want to convert them to equivalent 512 fft as if I did 512 fft. I also want do ifft similarly afterwards. Is it possible?
Regards
kaz

Hey Kaz:
I think that if you look carefully at what Rick is saying (well, if you look at the book -- I think the diagram is leaving out a step) you'll see that the actual FFT core isn't changed.

I think the answer has to be yes, but you have to be careful with how you scramble the data. You would do the first and second half blocks with elements (0..255) and (256..511), then scramble the elements between them (I'm betting alternating from each block, but I haven't done the math) and then run the two blocks again. Look at a butterfly chain for 8 and 16 elements and I bet you can see how to do it.

Hello Kaz,
Is it possible to choose the longer FFT size (512pts) and to zero pad the FFT in the case 256 pts?
A longer FFT size has more frequency bins.
FFT bins resolution (Hz) = SamplingFreq (Hz) / NbPoints (256 or 512)
I also implemented FFT and iFFT in FPGA using core ip (Xilinx) for match filtering and i agree it is more convenient to work with fixed FFT size.
Rgds,
Raph

Thanks Ralph,
That is an option on the table but we need the fft to finish early enough for 256 case. Duration of 512 is too much as we are doing column 2D fft on image followed by 2D ifft
Kaz

apologies Raph for misspelling your name.Also the word column in my above post should be dropped.
Kaz

Hi Kaz,
In this case, is it possible to implement 256pts FFT and proceed with overlap-add ?
More info: https://en.wikipedia.org/wiki/Overlap%E2%80%93add_...
The advantage is that you process by 256pts blocs.
This is method i used for streaming match filtering.
Rgds,
Raph

If you're doing a 512 complex in, 512 complex out, then you're using a too-complicated algorithm.
Isn't your data real? If so, a 512 real points in, 257 complex points out (0 to Fs/2) algorithm should be a bit faster -- possibly _enough_ faster that you could use it for both. You may want to dig a bit and see if Altera offers that as an option in their IP library.
To do a 256-point real FFT with a 512-point real FFT engine, just populate every other point with zeros in between -- the output will be two copies of the 256-point FFT.

I believe the term "zero padding" is a misstatement common to all textbooks (that I have seen) which should be replaced with "average padding". If taken literally on non-zero average data,zero padding introduces a step function which smears the spectrum with a bias that depends on its fundamental relative to the circular convolution size (i.e. number of samples). If it's one sample (or all but one), then you add an impulse to the "true" response). If data is prefiltered with a DC blocker before the FFT/DFT, then it should be "OK". Windowing can help to some extent (assuming it's done after padding), but tends on add its own artifacts.

In my case zero padding does the job. we are using fft/ifft to implement cross correlation of two images by multiplying in frequency domain instead of sliding whole two images in time domain. The technique works and requires zero padding for the two images to the size of correlation with padding being mirrored. The output of time domain sliding correlation is bit true copy of fft correlation.
Here I am not concerned about actual frequency contents but on equivalent operations.
Kaz
It is possible; however, I would suggest not do this. The reason is its complexity in performing 512 point FFT using 256 point engine. The steps are as below:
1. Perform a 256 point FFT on data n=0 to 255. Let the ffted data be X1FFT.
2. Perform a 256 point FFT on data n=256 to 511. Let the ffted data be X2FFT.
3. Take original time domain data n= 0 to 255, multiply with exp(-j * 2 * pi * n/512) and then take 256 point FFT. Let the ffted data be X11FFT.
4. Take original data n=256 to 512, multiply with exp(-j * 2 * pi * (n-256)/512) and then take 256 point FFT. let the ffted data be X22FFT.
After the four steps perform the following
X = zeros(512,1);
for m = 0 to 255
X(2*m) = X1FFT(m) + X2FFT(m) * exp(-1 * j * pi * 2* m);
X(2*m+1) = X11FFT(m) + X22FFT(m) * exp(-1 * j * pi * (2* m+1));
end
OR
for m = 0 to 255
X(2*m) = X1FFT(m) + X2FFT(m) ;
X(2*m+1) = X11FFT(m) - X22FFT(m) ;
end

Thanks LabPE43,
May I ask about the two cases of "OR", how could both cases be correct when case 1 asks for extra multiplications (exp(-1*j*2*m...).
And if you have also steps for IFFT of 512 points using 256 ifft that would be appreciated.
Kaz
The expression exp(-1 * j * pi * 2 * m) evaluates to 1 for all m as m is an integer (0 to 255). The expression exp(-1 * j * pi * (2*m+1)) evaluates to -1 for all m. These can be confirmed in matlab. So the two expression are equivalent.
For IFFT the steps are identical with -j or -1 * j replaced by j or 1 * j.
1. Perform a 256 point IFFT on data n=0 to 255. Let the iffted data be X1IFFT.
2. Perform a 256 point IFFT on data n=256 to 511. Let the iffted data be X2IFFT.
3. Take original time domain data n= 0 to 255, multiply with exp(j * 2 * pi * n/512) and then take 256 point IFFT. Let the iffted data be X11IFFT.
4. Take original data n=256 to 511, multiply with exp(j * 2 * pi * (n-256)/512) and then take 256 point IFFT. let the iffted data be X22IFFT.
After the four steps perform the following
x = zeros(512,1);
for m = 0 to 255
x(2*m) = X1IFFT(m) + X2IFFT(m) ;
x(2*m+1) = X11IFFT(m) - X22IFFT(m) ;
end

an old post, 6 years old...
8 is bin 8 of 256
0 is bin 0 (dc)
so 8 is relative to 256 and its tone = 8/256 *sampling rate applied to DFT.

Hi Kaz,
I can assure you, there are NO missing steps in the diagram I presented. The 1st step "unzips" the 2N-sample real-valued a(n) input sequence to generate an N-sample x(n) sequence as:
x(0) = a(0) + ja(1),
x(1) = a(2) + ja(3),
x(2) = a(4) + ja(5), and so on.
The 2nd step is your standard (canned) N-point complex-valued FFT. The 3rd step involves additions and divide-by-two operations. The 4th step involves multiplies by FFT twiddles factors plus some addition operations. Again, if you'd like to see the details of this whole process then just let me know.

Thanks Rick,
In my case I have "complex" input of 512 points and so it does not seem your diagram applies. Moreover I need do ifft of 512 using 256 ifft. And in all cases I need 512 points output.
Many thanks
Kaz


















