Reducing IIR Filter Computational Workload
This document describes a straightforward method to significantly reduce the number of necessary multiplies per input sample of traditional IIR lowpass and highpass digital filters.
An Experimental Multichannel Pulse Code Modulation System of Toll Quality + Electron Beam Deflection Tube For Pulse Code Modulation
See this blog post for context. Pulse Code Modulation offers attractive possibilities for multiplex telephony via such media as the microwave radio relay. The various problems involved in its use have been explored in terms of a 96-channel system designed to meet the transmission requirements commonly imposed upon commercial toll circuits. Twenty-four of the 96 channels have been fully equipped in an experimental model of the system. Coding and decoding devices are described, along with other circuit details. The coder is based upon a new electron beam tube, and is characterized by speed and simplicity as well as accuracy of coding. These qualities are matched in the decoder, which employs pulse excitation of a simple reactive network.
Use Matlab Function pwelch to Find Power Spectral Density - or Do It Yourself
In this article, I'll present some examples to show how to use pwelch. You can also "do it yourself", i.e. compute spectra using the Matlab fft or other fft function. As examples, the appendix provides two demonstration mfiles; one computes the spectrum without DFT averaging, and the other computes the spectrum with DFT averaging.
Design IIR Filters Using Cascaded Biquads
This article shows how to implement a Butterworth IIR lowpass filter as a cascade of second-order IIR filters, or biquads. We'll derive how to calculate the coefficients of the biquads and do some examples using a Matlab function biquad_synth provided in the Appendix. Although we'll be designing Butterworth filters, the approach applies to any all-pole lowpass filter (Chebyshev, Bessel, etc). As we'll see, the cascaded-biquad design is less sensitive to coefficient quantization than a single high-order IIR, particularly for lower cut-off frequencies.
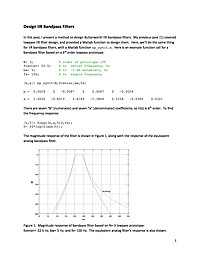
Design IIR Bandpass Filters
In this post, I present a method to design Butterworth IIR bandpass filters. My previous post [1] covered lowpass IIR filter design, and provided a Matlab function to design them. Here, we'll do the same thing for IIR bandpass filters, with a Matlab function bp_synth.m
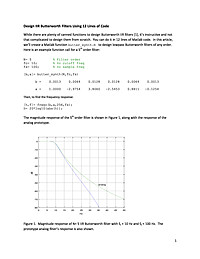
Design IIR Butterworth Filters Using 12 Lines of Code
While there are plenty of canned functions to design Butterworth IIR filters [1], it's instructive and not that complicated to design them from scratch. You can do it in 12 lines of Matlab code.
Algorithms, Architectures, and Applications for Compressive Video Sensing
The design of conventional sensors is based primarily on the Shannon-Nyquist sampling theorem, which states that a signal of bandwidth W Hz is fully determined by its discrete-time samples provided the sampling rate exceeds 2W samples per second. For discrete-time signals, the Shannon-Nyquist theorem has a very simple interpretation: the number of data samples must be at least as large as the dimensionality of the signal being sampled and recovered. This important result enables signal processing in the discrete-time domain without any loss of information. However, in an increasing number of applications, the Shannon-Nyquist sampling theorem dictates an unnecessary and often prohibitively high sampling rate. (See Box 1 for a derivation of the Nyquist rate of a time-varying scene.) As a motivating example, the high resolution of the image sensor hardware in modern cameras reflects the large amount of data sensed to capture an image. A 10-megapixel camera, in effect, takes 10 million measurements of the scene. Yet, almost immediately after acquisition, redundancies in the image are exploited to compress the acquired data significantly, often at compression ratios of 100:1 for visualization and even higher for detection and classification tasks. This example suggests immense wastage in the overall design of conventional cameras.
Multirate Systems and Filter Banks
During the last two decades, multirate filter banks have found various applications in many different areas, such as speech coding, scrambling, adaptive signal processing, image compression, signal and image processing applications as well as transmission of several signals through the same channel. The main idea of using multirate filter banks is the ability of the system to separate in the frequency domain the signal under consideration into two or more signals or to compose two or more different signals into a single signal.
A Review of Physical and Perceptual Feature Extraction Techniques for Speech, Music and Environmental Sounds
Endowing machines with sensing capabilities similar to those of humans is a prevalent quest in engineering and computer science. In the pursuit of making computers sense their surroundings, a huge effort has been conducted to allow machines and computers to acquire, process, analyze and understand their environment in a human-like way. Focusing on the sense of hearing, the ability of computers to sense their acoustic environment as humans do goes by the name of machine hearing. To achieve this ambitious aim, the representation of the audio signal is of paramount importance. In this paper, we present an up-to-date review of the most relevant audio feature extraction techniques developed to analyze the most usual audio signals: speech, music and environmental sounds. Besides revisiting classic approaches for completeness, we include the latest advances in the field based on new domains of analysis together with novel bio-inspired proposals. These approaches are described following a taxonomy that organizes them according to their physical or perceptual basis, being subsequently divided depending on the domain of computation (time, frequency, wavelet, image-based, cepstral, or other domains). The description of the approaches is accompanied with recent examples of their application to machine hearing related problems.
Peak-to-Average Power Ratio and CCDF
Peak to Average Power Ratio (PAPR) is often used to characterize digitally modulated signals. One example application is setting the level of the signal in a digital modulator. Knowing PAPR allows setting the average power to a level that is just low enough to minimize clipping.
Design IIR Bandpass Filters
In this post, I present a method to design Butterworth IIR bandpass filters. My previous post [1] covered lowpass IIR filter design, and provided a Matlab function to design them. Here, we'll do the same thing for IIR bandpass filters, with a Matlab function bp_synth.m
Digital PLL's - Part 2
In Part 1, we found the time response of a 2nd order PLL with a proportional + integral (lead-lag) loop filter. Now let's look at this PLL in the Z-domain.
Computing FFT Twiddle Factors
In this document are two algorithms showing how to compute the individual twiddle factors of an N-point decimation-in-frequency (DIF) and an N-point decimation-in-time (DIT) FFT.
Use Matlab Function pwelch to Find Power Spectral Density - or Do It Yourself
In this article, I'll present some examples to show how to use pwelch. You can also "do it yourself", i.e. compute spectra using the Matlab fft or other fft function. As examples, the appendix provides two demonstration mfiles; one computes the spectrum without DFT averaging, and the other computes the spectrum with DFT averaging.
Digital Signal Processor Fundamentals and System Design
Digital Signal Processors (DSPs) have been used in accelerator systems for more than fifteen years and have largely contributed to the evolution towards digital technology of many accelerator systems, such as machine protection, diagnostics and control of beams, power supply and motors. This paper aims at familiarising the reader with DSP fundamentals, namely DSP characteristics and processing development. Several DSP examples are given, in particular on Texas Instruments DSPs, as they are used in the DSP laboratory companion of the lectures this paper is based upon. The typical system design flow is described; common difficulties, problems and choices faced by DSP developers are outlined; and hints are given on the best solution.
C++ Tutorial
This tutorial is for those people who want to learn programming in C++ and do not necessarily have any previous knowledge of other programming languages. Of course any knowledge of other programming languages or any general computer skill can be useful to better understand this tutorial, although it is not essential. It is also suitable for those who need a little update on the new features the language has acquired from the latest standards. If you are familiar with the C language, you can take the first 3 parts of this tutorial as a review of concepts, since they mainly explain the C part of C++. There are slight differences in the C++ syntax for some C features, so I recommend you its reading anyway. The 4th part describes object-oriented programming. The 5th part mostly describes the new features introduced by ANSI-C++ standard.
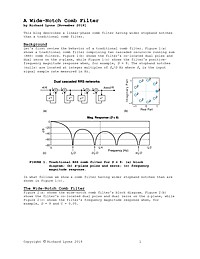
A Wide-Notch Comb Filter
This article describes a linear-phase comb filter having wider stopband notches than a traditional comb filter.
The Swiss Army Knife of Digital Networks
This article describes a general discrete-signal network that appears, in various forms, inside so many DSP applications.
