DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

The Four Direct Forms

Direct-Form I

As mentioned in §5.5, the difference equation

$\displaystyle y(n)$ $\displaystyle =$ $\displaystyle b_0 x(n) + b_1 x(n - 1) + \cdots + b_M x(n - M)$  
    $\displaystyle \qquad - a_1 y(n - 1) - \cdots - a_N y(n - N)$  
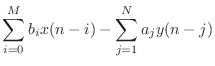  $\displaystyle =$ $\displaystyle \sum_{i=0}^M b_i x(n-i) - \sum_{j=1}^N a_j y(n-j)$ (10.1)

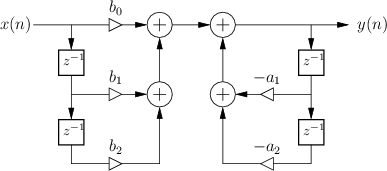
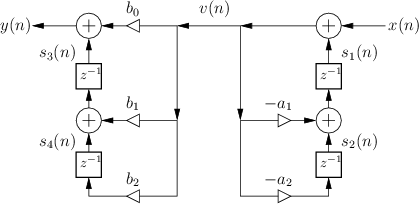
specifies the Direct-Form I (DF-I) implementation of a digital filter [60]. The DF-I signal flow graph for the second-order case is shown in Fig.9.1.

Figure 9.1: Direct-Form-I implementation of a 2nd-order digital filter.
\begin{figure}\input fig/df1.pstex_t \end{figure}

The DF-I structure has the following properties:

  1. It can be regarded as a two-zero filter section followed in series by a two-pole filter section.

  2. In most fixed-point arithmetic schemes (such as two's complement, the most commonly used [84]10.1) there is no possibility of internal filter overflow. That is, since there is fundamentally only one summation point in the filter, and since fixed-point overflow naturally ``wraps around'' from the largest positive to the largest negative number and vice versa, then as long as the final result $ y(n)$ is ``in range'', overflow is avoided, even when there is overflow of intermediate results in the sum (see below for an example). This is an important, valuable, and unusual property of the DF-I filter structure.

  3. There are twice as many delays as are necessary. As a result, the DF-I structure is not canonical with respect to delay. In general, it is always possible to implement an $ N$th-order filter using only $ N$ delay elements.

  4. As is the case with all direct-form filter structures (those which have coefficients given by the transfer-function coefficients), the filter poles and zeros can be very sensitive to round-off errors in the filter coefficients. This is usually not a problem for a simple second-order section, such as in Fig.9.1, but it can become a problem for higher order direct-form filters. This is the same numerical sensitivity that polynomial roots have with respect to polynomial-coefficient round-off. As is well known, the sensitivity tends to be larger when the roots are clustered closely together, as opposed to being well spread out in the complex plane [18, p. 246]. To minimize this sensitivity, it is common to factor filter transfer functions into series and/or parallel second-order sections, as discussed in §9.2 below.

It is a very useful property of the direct-form I implementation that it cannot overflow internally in two's complement fixed-point arithmetic: As long as the output signal is in range, the filter will be free of numerical overflow. Most IIR filter implementations do not have this property. While DF-I is immune to internal overflow, it should not be concluded that it is always the best choice of implementation. Other forms to consider include parallel and series second-order sections (§9.2 below), and normalized ladder forms [32,48,86].10.2Also, we'll see that the transposed direct-form II (Fig.9.4 below) is a strong contender as well.

Two's Complement Wrap-Around

In this section, we give an example showing how temporary overflow in two's complement fixed-point causes no ill effects.

In 3-bit signed fixed-point arithmetic, the available numbers are as shown in Table 9.1.


Table 9.1: Three-bit two's-complement binary fixed-point numbers.
Decimal Binary
-4 100
-3 101
-2 110
-1 111
0 000
1 001
2 010
3 011


Let's perform the sum $ 3+3-4 = 2$, which gives a temporary overflow ($ 3+3=6$, which wraps around to $ -2$), but a final result ($ 2$) which is in the allowed range $ [-4,3]$:10.3

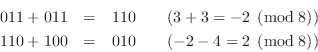
\begin{eqnarray*} 011 + 011 &=& 110 \qquad \mbox{$(3+3=-2\;\left(\mbox{mod}\;8\r... ...100 &=& 010 \qquad \mbox{$(-2-4=2\;\left(\mbox{mod}\;8\right))$} \end{eqnarray*}

Now let's do $ 1+3-2 = 2$ in three-bit two's complement:

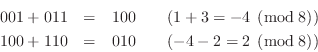
\begin{eqnarray*} 001 + 011 &=& 100 \qquad \mbox{$(1+3=-4\;\left(\mbox{mod}\;8\r... ...110 &=& 010 \qquad \mbox{$(-4-2=2\;\left(\mbox{mod}\;8\right))$} \end{eqnarray*}

In both examples, the intermediate result overflows, but the final result is correct. Another way to state what happened is that a positive wrap-around in the first addition is canceled by a negative wrap-around in the second addition.

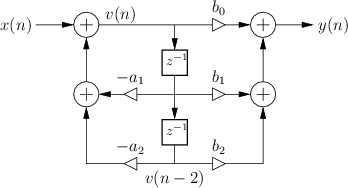
Direct Form II

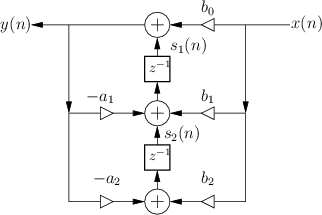
The signal flow graph for the Direct-Form-II (DF-II) realization of the second-order IIR filter section is shown in Fig.9.2.

Figure 9.2: Direct-Form-II implementation of a 2nd-order digital filter.
\begin{figure}\input fig/df2.pstex_t \end{figure}

The difference equation for the second-order DF-II structure can be written as

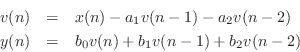
\begin{eqnarray*} v(n) &=& x(n) - a_1 v(n-1) - a_2 v(n-2)\\ y(n) &=& b_0 v(n) + b_1 v(n-1) + b_2 v(n-2) \end{eqnarray*}

which can be interpreted as a two-pole filter followed in series by a two-zero filter. This contrasts with the DF-I structure of the previous section (diagrammed in Fig.9.1) in which the two-zero FIR section precedes the two-pole recursive section in series. Since LTI filters in series commute (§6.7), we may reverse this ordering and implement an all-pole filter followed by an FIR filter in series. In other words, the zeros may come first, followed by the poles, without changing the transfer function. When this is done, it is easy to see that the delay elements in the two filter sections contain the same numbers (see Fig.5.1). As a result, a single delay line can be shared between the all-pole and all-zero (FIR) sections. This new combined structure is called ``direct form II'' [60, p. 153-155]. The second-order case is shown in Fig.9.2. It specifies exactly the same digital filter as shown in Fig.9.1 in the case of infinite-precision numerical computations.

In summary, the DF-II structure has the following properties:

  1. It can be regarded as a two-pole filter section followed by a two-zero filter section.

  2. It is canonical with respect to delay. This happens because delay elements associated with the two-pole and two-zero sections are shared.

  3. In fixed-point arithmetic, overflow can occur at the delay-line input (output of the leftmost summer in Fig.9.2), unlike in the DF-I implementation.

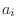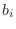  4. As with all direct-form filter structures, the poles and zeros are sensitive to round-off errors in the coefficients $ a_i$ and $ b_i$, especially for high transfer-function orders. Lower sensitivity is obtained using series low-order sections (e.g., second order), or by using ladder or lattice filter structures [86].

More about Potential Internal Overflow of DF-II

Since the poles come first in the DF-II realization of an IIR filter, the signal entering the state delay-line (see Fig.9.2) typically requires a larger dynamic range than the output signal $ y(n)$. In other words, it is common for the feedback portion of a DF-II IIR filter to provide a large signal boost which is then compensated by attenuation in the feedforward portion (the zeros). As a result, if the input dynamic range is to remain unrestricted, the two delay elements may need to be implemented with high-order guard bits to accommodate an extended dynamic range. If the number of bits in the delay elements is doubled (which still does not guarantee impossibility of internal overflow), the benefit of halving the number of delays relative to the DF-I structure is approximately canceled. In other words, the DF-II structure, which is canonical with respect to delay, may require just as much or more memory as the DF-I structure, even though the DF-I uses twice as many addressable delay elements for the filter state memory.

Transposed Direct-Forms

The remaining two direct forms are obtained by formally transposing direct-forms I and II [60, p. 155]. Filter transposition may also be called flow graph reversal, and transposing a Single-Input, Single-Output (SISO) filter does not alter its transfer function. This fact can be derived as a consequence of Mason's gain formula for signal flow graphs [49,50] or Tellegen's theorem (which implies that an LTI signal flow graph is interreciprocal with its transpose) [60, pp. 176-177]. Transposition of filters in state-space form is discussed in §G.5.

The transpose of a SISO digital filter is quite straightforward to find: Reverse the direction of all signal paths, and make obviously necessary accommodations. ``Obviously necessary accommodations'' include changing signal branch-points to summers, and summers to branch-points. Also, after this operation, the input signal, normally drawn on the left of the signal flow graph, will be on the right, and the output on the left. To renormalize the layout, the whole diagram is usually left-right flipped.

Figure 9.3 shows the Transposed-Direct-Form-I (TDF-I) structure for the general second-order IIR digital filter, and Fig.9.4 shows the Transposed-Direct-Form-II (TDF-II) structure. To facilitate comparison of the transposed with the original, the inputs and output signals remain ``switched'', so that signals generally flow right-to-left instead of the usual left-to-right. (Exercise: Derive forms TDF-I/II by transposing the DF-I/II structures shown in Figures 9.1 and 9.2.)

Figure: Transposed-Direct-Form-I implementation of a second-order IIR digital filter. Note that the input signal comes in from the right, and the output is on the left. Compare to Fig.9.1. The four ``state variable'' signals are labeled arbitrarily as $ s_1(n)$ through $ s_4(n)$.
\begin{figure}\input fig/tdfi.pstex_t \end{figure}

Figure: Transposed-Direct-Form-II implementation of a second-order IIR digital filter (input on the right, output on the left). Compare to Fig.9.2.
\begin{figure}\input fig/tdfii.pstex_t \end{figure}

Numerical Robustness of TDF-II

An advantage of the transposed direct-form II structure (depicted in Fig.9.4) is that the zeros effectively precede the poles in series order. As mentioned above, in many digital filters design, the poles by themselves give a large gain at some frequencies, and the zeros often provide compensating attenuation. This is especially true of filters with sharp transitions in their frequency response, such as the elliptic-function-filter example on page [*]; in such filters, the sharp transitions are achieved using near pole-zero cancellations close to the unit circle in the $ z$ plane.10.4

Next Section:
Series and Parallel Filter Sections
Previous Section:
Pole-Zero Analysis Problems