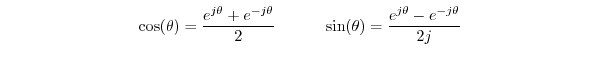Free Books    Mathematics of the DFT  

Complex Numbers

This chapter introduces complex numbers, beginning with factoring polynomials, and proceeding on to the complex plane and Euler's identity.

Factoring a Polynomial

Remember ``factoring polynomials''? Consider the second-order polynomial

$\displaystyle p(x) = x^2-5x+6. $

It is second-order because the highest power of $ x$ is $ 2$ (only non-negative integer powers of $ x$ are allowed in this context). The polynomial is also monic because its leading coefficient, the coefficient of $ x^2$, is $ 1$. By the fundamental theorem of algebra (discussed further in §2.4), there are exactly two roots (or zeros) of any second order polynomial. These roots may be real or complex (to be defined). For now, let's assume they are both real and denote them by $ r_1$ and $ r_2$. Then we have $ p(r_1)=0$ and $ p(r_2)=0$, and we can write

$\displaystyle p(x) = (x-r_1)(x-r_2). $

This is the factored form of the monic polynomial $ p(x)$. (For a non-monic polynomial, we may simply divide all coefficients by the first to make it monic, and this doesn't affect the zeros.) Multiplying out the symbolic factored form gives

$\displaystyle p(x) = (x-r_1)(x-r_2) = x^2 - (r_1 + r_2)x + r_1 r_2. $

Comparing with the original polynomial, we find we must have

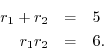
\begin{eqnarray*} r_1+r_2 &=& 5 \\ r_1 r_2 &=& 6. \end{eqnarray*}

This is a system of two equations in two unknowns. Unfortunately, it is a nonlinear system of two equations in two unknowns.2.1 Nevertheless, because it is so small, the equations are easily solved. In beginning algebra, we did them by hand. However, nowadays we can use a software tool such as Matlab or Octave to solve very large systems of linear equations.

The factored form of this simple example is

$\displaystyle p(x) = x^2-5x+6 = (x-r_1)(x-r_2) = (x-2)(x-3). $

Note that polynomial factorization rewrites a monic $ n$th-order polynomial as the product of $ n$ first-order monic polynomials, each of which contributes one zero (root) to the product. This factoring business is often used when working with digital filters [68].

The Quadratic Formula

The general second-order (real) polynomial is

$\displaystyle p(x) \isdef a x^2 + b x + c \protect$ (2.1)

where the coefficients $ a,b,c$ are any real numbers, and we assume $ a\neq 0$ since otherwise it would not be second order. Some experiments plotting $ p(x)$ for different values of the coefficients leads one to guess that the curve is always a scaled and translated parabola. The canonical parabola centered at $ x=x_0$ is given by

$\displaystyle y(x) = d\cdot (x-x_0)^2 + e \protect$ (2.2)

where the magnitude of $ d$ determines the width of the parabola, and $ e$ provides an arbitrary vertical offset. If $ d>0$, the parabola has the minimum value $ e$ at $ x=x_0$; when $ d<0$, the parabola reaches a maximum at $ x=x_0$ (also equal to $ e$). If we can find $ d,e,x_0$ in terms of $ a,b,c$ for any quadratic polynomial, then we can easily factor the polynomial. This is called completing the square. Multiplying out the right-hand side of Eq.$ \,$(2.2) above, we get

$\displaystyle y(x) = d(x-x_0)^2 + e = d x^2 -2 d x_0 x + d x_0^2 + e. \protect$ (2.3)

Equating coefficients of like powers of $ x$ to the general second-order polynomial in Eq.$ \,$(2.1) gives

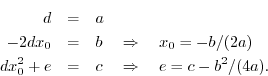
\begin{eqnarray*} d &=& a\\ -2 d x_0 &=& b \quad\Rightarrow\quad x_0 = -b/(2a) \\ d x_0^2 + e &=& c \quad\Rightarrow\quad e = c - b^2/(4a). \end{eqnarray*}

Using these answers, any second-order polynomial $ p(x) = a x^2 + b x + c$ can be rewritten as a scaled, translated parabola

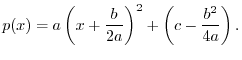
$\displaystyle p(x) = a\left(x+\frac{b}{2a}\right)^2 + \left(c - \frac{b^2}{4a}\right). $

In this form, the roots are easily found by solving $ p(x)=0$ to get

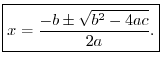
$\displaystyle \zbox {x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}.} $

This is the general quadratic formula. It was obtained by simple algebraic manipulation of the original polynomial. There is only one ``catch.'' What happens when $ b^2 - 4ac$ is negative? This introduces the square root of a negative number which we could insist ``does not exist.'' Alternatively, we could invent complex numbers to accommodate it.

Complex Roots

Figure 2.1: An example parabola defined by $ p(x) = x^2 + 4$.
\includegraphics[scale=0.5]{eps/parabola}

As a simple example, let $ a=1$, $ b=0$, and $ c=4$, i.e.,

$\displaystyle p(x) = x^2 + 4. $

As shown in Fig.2.1, this is a parabola centered at $ x=0$ (where $ p(0)=4$) and reaching upward to positive infinity, never going below $ 4$. It has no real zeros. On the other hand, the quadratic formula says that the ``roots'' are given formally by $ x=\pm\sqrt{-4} = \pm 2 \sqrt{-1}$. The square root of any negative number $ c<0$ can be expressed as $ \sqrt{\left\vert c\right\vert}\sqrt{-1}$, so the only new algebraic object is $ \sqrt{-1}$. Let's give it a name:

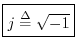
$\displaystyle \zbox {j \isdef \sqrt{-1}} $

Then, formally, the roots of $ x^2 + 4$ are $ \pm 2j$, and we can formally express the polynomial in terms of its roots as

$\displaystyle p(x) = (x+2j)(x-2j). $

We can think of these as ``imaginary roots'' in the sense that square roots of negative numbers don't really exist, or we can extend the concept of ``roots'' to allow for complex numbers, that is, numbers of the form

$\displaystyle z = x + j y $

where $ x$ and $ y$ are real numbers, and $ j^2\isdef -1$.

It can be checked that all algebraic operations for real numbers2.2 apply equally well to complex numbers. Both real numbers and complex numbers are examples of a mathematical field.2.3 Fields are closed with respect to multiplication and addition, and all the rules of algebra we use in manipulating polynomials with real coefficients (and roots) carry over unchanged to polynomials with complex coefficients and roots. In fact, the rules of algebra become simpler for complex numbers because, as discussed in the next section, we can always factor polynomials completely over the field of complex numbers while we cannot do this over the reals (as we saw in the example $ p(x) = x^2 + 4$).

Fundamental Theorem of Algebra

\fbox{\emph{Every $n$th-order polynomial possesses exactly $n$\ complex roots.}}
This is a very powerful algebraic tool.2.4 It says that given any polynomial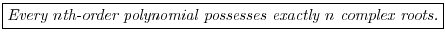

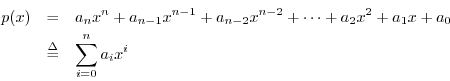
\begin{eqnarray*} p(x) &=& a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + \cdots + a_2 x^2 + a_1 x + a_0 \\ &\isdef & \sum_{i=0}^n a_i x^i \end{eqnarray*}

we can always rewrite it as

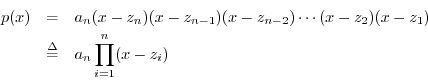
\begin{eqnarray*} p(x) &=& a_n (x - z_n) (x - z_{n-1}) (x - z_{n-2}) \cdots (x - z_2) (x - z_1) \\ &\isdef & a_n \prod_{i=1}^n (x-z_i) \end{eqnarray*}

where the points $ z_i$ are the polynomial roots, and they may be real or complex.

Complex Basics

This section introduces various notation and terms associated with complex numbers. As discussed above, complex numbers arise by introducing the square-root of $ -1$ as a primitive new algebraic object among real numbers and manipulating it symbolically as if it were a real number itself:

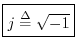
$\displaystyle \zbox {j \isdef \sqrt{-1}} $

Mathematicians and physicists often use $ i$ instead of $ j$ as $ \sqrt{-1}$. The use of $ j$ is common in engineering where $ i$ is more often used for electrical current.

As mentioned above, for any negative number $ c<0$, we have

$\displaystyle \sqrt{c} = \sqrt{(-1)(-c)} = j\sqrt{-c} = j\sqrt{\left\vert c\right\vert}, $

where $ \left\vert c\right\vert$ denotes the absolute value of $ c$. Thus, every square root of a negative number can be expressed as $ j$ times the square root of a positive number.

By definition, we have

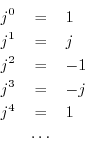
\begin{eqnarray*} j^0 &=& 1 \\ j^1 &=& j \\ j^2 &=& -1 \\ j^3 &=& -j\\ j^4 &=& 1 \\ &\cdots& \end{eqnarray*}

and so on. Thus, the sequence $ x(n)\isdef j^n$, $ n=0,1,2,\ldots$ is a periodic sequence with period $ 4$, since $ j^{n+4}=j^n j^4=j^n$. (We'll learn later that the sequence $ j^n$ is a sampled complex sinusoid having frequency equal to one fourth the sampling rate.)

Every complex number $ z$ can be written as

$\displaystyle \zbox {z = x + j y} $

where $ x$ and $ y$ are real numbers. We call $ x$ the real part and $ y$ the imaginary part. We may also use the notation

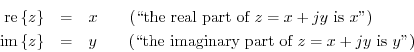
\begin{eqnarray*} \mbox{re}\left\{z\right\} &=& x \qquad \mbox{(\lq\lq the real part ... ...&=& y \qquad \mbox{(\lq\lq the imaginary part of $z=x+jy$\ is $y$'')} \end{eqnarray*}

Note that the real numbers are the subset of the complex numbers having a zero imaginary part ($ y=0$).

The rule for complex multiplication follows directly from the definition of the imaginary unit $ j$:

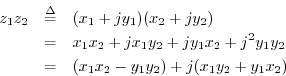
\begin{eqnarray*} z_1 z_2 &\isdef & (x_1 + j y_1) (x_2 + j y_2) \\ &=& x_1 x_2... ...j^2 y_1 y_2 \\ &=& (x_1 x_2 - y_1 y_2) + j (x_1 y_2 + y_1 x_2) \end{eqnarray*}

In some mathematics texts, complex numbers $ z$ are defined as ordered pairs of real numbers $ (x,y)$, and algebraic operations such as multiplication are defined more formally as operations on ordered pairs, e.g., $ (x_1,y_1) \cdot (x_2,y_2) \isdeftext (x_1 x_2 - y_1 y_2, x_1 y_2 + y_1 x_2)$. However, such formality tends to obscure the underlying simplicity of complex numbers as a straightforward extension of real numbers to include $ j\isdeftext \sqrt{-1}$.

It is important to realize that complex numbers can be treated algebraically just like real numbers. That is, they can be added, subtracted, multiplied, divided, etc., using exactly the same rules of algebra (since both real and complex numbers are mathematical fields). It is often preferable to think of complex numbers as being the true and proper setting for algebraic operations, with real numbers being the limited subset for which $ y=0$.

The Complex Plane

Figure 2.2: Plotting a complex number as a point in the complex plane.
\includegraphics[scale=0.5]{eps/ComplexPlane}

We can plot any complex number $ z = x + jy$ in a plane as an ordered pair $ (x,y)$, as shown in Fig.2.2. A complex plane (or Argand diagram) is any 2D graph in which the horizontal axis is the real part and the vertical axis is the imaginary part of a complex number or function. As an example, the number $ j$ has coordinates $ (0,1)$ in the complex plane while the number $ 1$ has coordinates $ (1,0)$.

Plotting $ z = x + jy$ as the point $ (x,y)$ in the complex plane can be viewed as a plot in Cartesian or rectilinear coordinates. We can also express complex numbers in terms of polar coordinates as an ordered pair $ (r,\theta)$, where $ r$ is the distance from the origin $ (0,0)$ to the number being plotted, and $ \theta$ is the angle of the number relative to the positive real coordinate axis (the line defined by $ y=0$ and $ x>0$). (See Fig.2.2.)

Using elementary geometry, it is quick to show that conversion from rectangular to polar coordinates is accomplished by the formulas

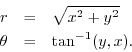
\begin{eqnarray*} r &=& \sqrt{x^2 + y^2}\\ \theta &=& \tan^{-1}(y,x). \end{eqnarray*}

where $ \tan^{-1}(y,x)$ denotes the arctangent of $ y/x$ (the angle $ \theta$ in radians whose tangent is $ \tan(\theta)=y/x$), taking the quadrant of the vector $ (x,y)$ into account. We will take $ \theta$ in the range $ -\pi$ to $ \pi $ (although we could choose any interval of length $ 2\pi $ radians, such as 0 to $ 2\pi $, etc.).

In Matlab and Octave, atan2(y,x) performs the ``quadrant-sensitive'' arctangent function. On the other hand, atan(y/x), like the more traditional mathematical notation $ \tan^{-1}(y/x)$ does not ``know'' the quadrant of $ (x,y)$, so it maps the entire real line to the interval $ (-\pi/2,\pi/2)$. As a specific example, the angle of the vector $ (x,y)=(1,1)$ (in quadrant I) has the same tangent as the angle of $ (x,y)=(-1,-1)$ (in quadrant III). Similarly, $ (x,y)=(-1,1)$ (quadrant II) yields the same tangent as $ (x,y)=(1,-1)$ (quadrant IV).

The formula $ r = \sqrt{x^2 + y^2}$ for converting rectangular coordinates to radius $ r$, follows immediately from the Pythagorean theorem, while the $ \theta = \tan^{-1}(y,x)$ follows from the definition of the tangent function itself.

Similarly, conversion from polar to rectangular coordinates is simply

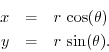
\begin{eqnarray*} x &=& r\,\cos(\theta)\\ y &=& r\,\sin(\theta). \end{eqnarray*}

These follow immediately from the definitions of cosine and sine, respectively.

More Notation and Terminology

It's already been mentioned that the rectilinear coordinates of a complex number $ z = x + jy$ in the complex plane are called the real part and imaginary part, respectively.

We also have special notation and various names for the polar coordinates $ (r,\theta)$ of a complex number $ z$:

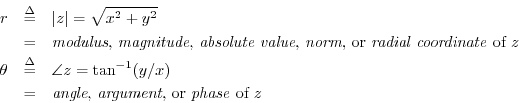
\begin{eqnarray*} r &\isdef & \left\vert z\right\vert = \sqrt{x^2 + y^2}\\ &=&... ...!argument, angle, or phase\vert textbf}, or \emph{phase} of $z$} \end{eqnarray*}

The complex conjugate of $ z$ is denoted $ \overline{z}$ (or $ z^\ast$) and is defined by

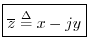
$\displaystyle \zbox {\overline{z} \isdef x - j y} $

where, of course, $ z\isdef x+jy$.

In general, you can always obtain the complex conjugate of any expression by simply replacing $ j$ with $ -j$. In the complex plane, this is a vertical flip about the real axis; i.e., complex conjugation replaces each point in the complex plane by its mirror image on the other side of the $ x$ axis.

Elementary Relationships

From the above definitions, one can quickly verify

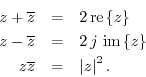
\begin{eqnarray*} z+\overline{z} &=& 2 \, \mbox{re}\left\{z\right\} \\ z-\overl... ...left\{z\right\} \\ z\overline{z} &=& \left\vert z\right\vert^2. \end{eqnarray*}

Let's verify the third relationship which states that a complex number multiplied by its conjugate is equal to its magnitude squared:

$\displaystyle z \overline{z} \isdef (x+jy)(x-jy) = x^2-(jy)^2 = x^2 + y^2 \isdef \vert z\vert^2 \protect$ (2.4)

Euler's Identity

Since $ z = x + jy$ is the algebraic expression of $ z$ in terms of its rectangular coordinates, the corresponding expression in terms of its polar coordinates is

$\displaystyle z = r\cos(\theta) + j\,r\sin(\theta). $

There is another, more powerful representation of $ z$ in terms of its polar coordinates. In order to define it, we must introduce Euler's identity:

$\displaystyle \zbox {e^{j\theta}=\cos(\theta)+j\sin(\theta)}$ (2.5)

A proof of Euler's identity is given in the next chapter. Before, the only algebraic representation of a complex number we had was $ z = x + jy$, which fundamentally uses Cartesian (rectilinear) coordinates in the complex plane. Euler's identity gives us an alternative representation in terms of polar coordinates in the complex plane:

$\displaystyle \zbox {z = re^{j\theta}} $

We'll call $ re^{j\theta}$ the polar form of the complex number $ z$, in contrast with the rectangular form $ z = x + jy$. Polar form often simplifies algebraic manipulations of complex numbers, especially when they are multiplied together. Simple rules of exponents can often be used in place of messier trigonometric identities. In the case of two complex numbers being multiplied, we have

$\displaystyle z_1 z_2 = \left(r_1 e^{j \theta_1}\right) \left(r_2 e^{j \theta_... ...ta_1} e^{j \theta_2}\right) = r_1 r_2 e^{j \left(\theta_1 + \theta_2\right)}. $

A corollary of Euler's identity is obtained by setting $ \theta=\pi$ to get

$\displaystyle e^{j\pi} + 1 = 0. $

This has been called the ``most beautiful formula in mathematics'' due to the extremely simple form in which the fundamental constants $ e, j, \pi, 1$, and 0, together with the elementary operations of addition, multiplication, exponentiation, and equality, all appear exactly once.

For another example of manipulating the polar form of a complex number, let's again verify $ z\overline{z} = \left\vert z\right\vert^2$, as we did above in Eq.$ \,$(2.4), but this time using polar form:

$\displaystyle z \overline{z} = r e^{j \theta} r e^{-j \theta} = r^2 e^0 = r^2 = \vert z\vert^2 $

As mentioned in §2.7, any complex expression can be conjugated by replacing $ j$ by $ -j$ wherever it occurs. This implies $ \overline{r e^{j \theta}} = r e^{-j \theta}$, as used above. The same result can be obtained by using Euler's identity to expand $ re^{j\theta}$ into $ r \cos(\theta) + j r \sin(\theta)$ and negating the imaginary part to obtain $ \overline{r e^{j\theta}} = r \cos(\theta) - j r \sin(\theta) = r \cos(-\theta) + j r \sin(-\theta) = r e^{-j \theta}$, where we used also the fact that cosine is an even function ( $ \cos(-\theta) = \cos(\theta)$) while sine is odd ( $ \sin(-\theta) = -\sin(\theta)$).

We can now easily add a fourth line to that set of examples:

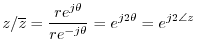
$\displaystyle z/\overline{z} = \frac{r e^{j \theta}}{r e^{-j \theta}} = e^{j2\theta} = e^{j2\angle{z}} $

Thus, $ \left\vert z/\overline{z}\right\vert=1$ for every $ z\neq 0$.

Euler's identity can be used to derive formulas for sine and cosine in terms of $ e^{j\theta }$:

\begin{eqnarray*} e^{j \theta} + \overline{e^{j \theta}}&=&e^{j \theta} + e^{-j ... ...+ \left[\cos(\theta) - j \sin(\theta)\right]\\ &=&2\cos(\theta) \end{eqnarray*}

Similarly, $ e^{j \theta} - \overline{e^{j \theta}} = 2j\, \sin(\theta)$, and we obtain the following classic identities:

$\textstyle \parbox{0.8\textwidth}{% \begin{displaymath} \cos(\theta) = \display... ...heta) = \displaystyle\frac{e^{j \theta} - e^{-j \theta}}{2j} \end{displaymath}}$

De Moivre's Theorem

As a more complicated example of the value of the polar form, we'll prove De Moivre's theorem:

$\displaystyle \left[\cos(\theta) + j \sin(\theta)\right] ^n = \cos(n\theta) + j \sin(n\theta) $

Working this out using sum-of-angle identities from trigonometry is laborious (see §3.13 for details). However, using Euler's identity, De Moivre's theorem simply ``falls out'':

$\displaystyle \left[\cos(\theta) + j \sin(\theta)\right] ^n = \left[e^{j\theta}\right] ^n = e^{j\theta n} = \cos(n\theta) + j \sin(n\theta) $

Moreover, by the power of the method used to show the result, $ n$ can be any real number, not just an integer.

Conclusion

This chapter has covered just enough about complex numbers to enable us to talk about the discrete Fourier transform.

Manipulations of complex numbers in Matlab and Octave are illustrated in §I.1.

To explore further the mathematics of complex variables, see any textbook such as Churchill [15] or LePage [37]. Topics not covered here, but which are important elsewhere in signal processing, include analytic functions, contour integration, analytic continuation, residue calculus, and conformal mapping.

Complex_Number Problems

See http://ccrma.stanford.edu/~jos/mdftp/Complex_Number_Problems.html

Next Section:
Proof of Euler's Identity
Previous Section:
Introduction to the DFT