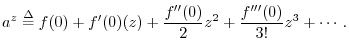Free Books Mathematics of the DFT

Proof of Euler's Identity

This chapter outlines the proof of Euler's Identity, which is an important tool for working with complex numbers. It is one of the critical elements of the DFT definition that we need to understand.

Euler's Identity

Euler's identity (or ``theorem'' or ``formula'') is

$\displaystyle e^{j\theta} = \cos(\theta) + j\sin(\theta)$ (Euler's Identity)

To ``prove'' this, we will first define what we mean by `` $e^{j\theta }$ ''. (The right-hand side, $\cos(\theta) + j\sin(\theta)$ , is assumed to be understood.) Since

is just a particular real number, we only really have to explain what we mean by imaginary exponents. (We'll also see where

comes from in the process.) Imaginary exponents will be obtained as a generalization of real exponents. Therefore, our first task is to define exactly what we mean by

, where

is any real number, and

is any positive real number.

Positive Integer Exponents

The ``original'' definition of exponents which ``actually makes sense'' applies only to positive integer exponents:

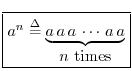
$\displaystyle \zbox {a^n \isdef \underbrace{a\, a \, a \,\cdots \,a \, a}_{\mbox{$n$\ times}}}$

where

is real.

Generalizing this definition involves first noting its abstract mathematical properties, and then making sure these properties are preserved in the generalization.

Properties of Exponents

From the basic definition of positive integer exponents, we have

(1): $a^{n_1} a^{n_2} = a^{n_1 + n_2}$
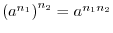
(2): $\left(a^{n_1}\right)^{n_2} = a^{n_1 n_2}$

Note that property (1) implies property (2). We list them both explicitly for convenience below.

The Exponent Zero

How should we define in a manner consistent with the properties of integer exponents? Multiplying it by gives

$\displaystyle a^0 a = a^0 a^1 = a^{0+1} = a^1 = a$

by property (1) of exponents. Solving

for

then gives

$\displaystyle \zbox {a^0 = 1.}$

Negative Exponents

What should $a^{-1}$ be? Multiplying it by gives, using property (1),

$\displaystyle a^{-1} \cdot a = a^{-1} a^1 = a^{-1+1} = a^0 = 1.$

Dividing through by

then gives

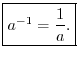
$\displaystyle \zbox {a^{-1} = \frac{1}{a}.}$

Similarly, we obtain

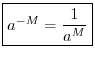
$\displaystyle \zbox {a^{-M} = \frac{1}{a^M}}$

for all integer values of

, i.e., $\forall M\in{\bf Z}$ .

Rational Exponents

A rational number is a real number that can be expressed as a ratio of two finite integers:

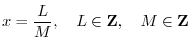
$\displaystyle x = \frac{L}{M}, \quad L\in{\bf Z},\quad M\in{\bf Z}$

Applying property (2) of exponents, we have

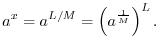
$\displaystyle a^x = a^{L/M} = \left(a^{\frac{1}{M}}\right)^L.$

Thus, the only thing new is $a^{1/M}$ . Since

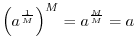
$\displaystyle \left(a^{\frac{1}{M}}\right)^M = a^{\frac{M}{M}} = a$

we see that $a^{1/M}$ is the

th root of

. This is sometimes written

$\displaystyle \zbox {a^{\frac{1}{M}} \isdef \sqrt[M]{a}.}$

The

th root of a real (or complex) number is not unique. As we all know, square roots give two values (e.g., $\sqrt{4}=\pm2$ ). In the general case of

th roots, there are

distinct values, in general. After proving Euler's identity, it will be easy to find them all (see §3.11). As an example, $\sqrt[4]{1}=1$ ,

, and

, since

The closest we can actually get to most real numbers is to compute a rational number that is as close as we need. It can be shown that rational numbers are dense in the real numbers; that is, between every two real numbers there is a rational number, and between every two rational numbers is a real number.^3.1An irrational number can be defined as any real number having a non-repeating decimal expansion. For example, $\sqrt{2}$ is an irrational real number whose decimal expansion starts out as^3.2

$\displaystyle \sqrt{2} = 1.414213562373095048801688724209698078569671875376948073176679\dots$

Every truncated, rounded, or repeating expansion is a rational number. That is, it can be rewritten as an integer divided by another integer. For example,

$\displaystyle 1.414 = \frac{1414}{1000}$

and, using $\overline{\mbox{overbar}}$ to denote the repeating part of a decimal expansion, a repeating example is as follows:

$\begin{eqnarray*} x &=& 0.\overline{123} \\ [5pt] \quad\Rightarrow\quad 1000x &=... ...999x &=& 123\\ [5pt] \quad\Rightarrow\quad x &=& \frac{123}{999} \end{eqnarray*}$

Other examples of irrational numbers include

$\begin{eqnarray*} \pi &=& 3.1415926535897932384626433832795028841971693993751058... ...82818284590452353602874713526624977572470936999595749669\dots\,. \end{eqnarray*}$

Their decimal expansions do not repeat.

Let ${\hat x}_n$ denote the -digit decimal expansion of an arbitrary real number . Then ${\hat x}_n$ is a rational number (some integer over ). We can say

$\displaystyle \lim_{n\to\infty} {\hat x}_n = x.$

That is, the limit of ${\hat x}_n$ as

goes to infinity is

Since $a^{{\hat x}_n}$ is defined for all , we naturally define as the following mathematical limit:

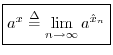
$\displaystyle \zbox {a^x \isdef \lim_{n\to\infty} a^{{\hat x}_n}}$

We have now defined what we mean by real exponents.

A First Look at Taylor Series

Most ``smooth'' functions can be expanded in the form of a Taylor series expansion:

$\displaystyle f(x) = f(x_0) + \frac{f^\prime(x_0)}{1}(x-x_0) + \frac{f^{\prim... ... + \frac{f^{\prime\prime\prime}(x_0)}{1\cdot 2\cdot 3}(x-x_0)^3 + \cdots .$

This can be written more compactly as

$\displaystyle f(x) = \sum_{n=0}^\infty \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n,$

where `

' is pronounced ``

factorial''. An informal derivation of this formula for

is given in Appendix E. Clearly, since many derivatives are involved, a Taylor series expansion is only possible when the function is so smooth that it can be differentiated again and again. Fortunately for us, all audio signals are in that category, because hearing is bandlimited to below

kHz, and the audible spectrum of any sum of sinusoids is infinitely differentiable. (Recall that $\sin^\prime(x)=\cos(x)$ and $\cos^\prime(x)=-\sin(x)$ , etc.). See §E.6 for more about this point.

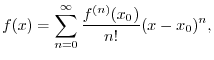
Imaginary Exponents

We may define imaginary exponents the same way that all sufficiently smooth real-valued functions of a real variable are generalized to the complex case--using Taylor series. A Taylor series expansion is just a polynomial (possibly of infinitely high order), and polynomials involve only addition, multiplication, and division. Since these elementary operations are also defined for complex numbers, any smooth function of a real variable may be generalized to a function of a complex variable by simply substituting the complex variable for the real variable in the Taylor series expansion of .

Let $f(x) \isdef a^x$ , where is any positive real number and is real. The Taylor series expansion about (``Maclaurin series''), generalized to the complex case is then

$\displaystyle a^z \isdef f(0)+f^\prime(0)(z) + \frac{f^{\prime\prime}(0)}{2}z^2 + \frac{f^{\prime\prime\prime}(0)}{3!}z^3 + \cdots\,. \protect$

(3.1)

This is well defined, provided the series converges for every finite

(see Problem 8). We have $f(0) \isdeftext a^0 = 1$ , so the first term is no problem. But what is $f^\prime(0)$ ? In other words, what is the derivative of

? Once we find the successive derivatives of $f(x) \isdeftext a^x$ at

, we will have the definition of

for any complex

Derivatives of f(x)=a^x

Let's apply the definition of differentiation and see what happens:

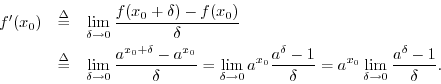
$\begin{eqnarray*} f^\prime(x_0) &\isdef & \lim_{\delta\to0} \frac{f(x_0+\delta)-... ...{\delta} = a^{x_0}\lim_{\delta\to0} \frac{a^\delta-1}{\delta}. \end{eqnarray*}$

Since the limit of $(a^\delta-1)/\delta$ as $\delta\to 0$ is less than 1 for and greater than for (as one can show via direct calculations), and since $(a^\delta-1)/\delta$ is a continuous function of for $\delta>0$ , it follows that there exists a positive real number we'll call such that for we get

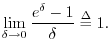
$\displaystyle \lim_{\delta\to 0} \frac{e^\delta-1}{\delta} \isdef 1 .$

For

, we thus have $\left(a^x\right)^\prime = (e^x)^\prime = e^x$ .

So far we have proved that the derivative of is . What about for other values of ? The trick is to write it as

$\displaystyle a^x = e^{\ln\left(a^x\right)}=e^{x\ln(a)}$

and use the chain rule,^3.3 where $\ln(a)\isdef \log_e(a)$ denotes the log-base-

.^3.4 Formally, the chain rule tells us how to differentiate a function of a function as follows:

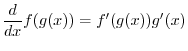
$\displaystyle \frac{d}{dx} f(g(x)) = f^\prime(g(x)) g^\prime(x)$

Evaluated at a particular point

, we obtain

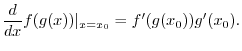
$\displaystyle \frac{d}{dx} f(g(x))\vert _{x=x_0} = f^\prime(g(x_0)) g^\prime(x_0).$

In this case, $g(x)=x\ln(a)$ so that $g^\prime(x) = \ln(a)$ , and

which is its own derivative. The end result is then $\left(a^x\right)^\prime = \left(e^{x\ln a}\right)^\prime = e^{x\ln(a)}\ln(a) = a^x \ln(a)$ , i.e.,

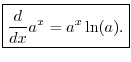
$\displaystyle \zbox {\frac{d}{dx} a^x = a^x \ln(a).}$

Back to e

Above, we defined as the particular real number satisfying

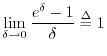
$\displaystyle \lim_{\delta\to 0} \frac{e^\delta-1}{\delta} \isdef 1$

which gave us $(a^x)^\prime = a^x$ when

. From this expression, we have, as $\delta\to 0$ ,

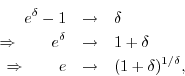
$\begin{eqnarray*} e^\delta - 1 & \rightarrow & \delta \\ \Rightarrow \qquad e^... ... \\ \Rightarrow \qquad e & \rightarrow & (1+\delta)^{1/\delta}, \end{eqnarray*}$

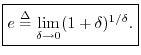
$\displaystyle \zbox {e \isdef \lim_{\delta\to0} (1+\delta)^{1/\delta}.}$

This is one way to define

. Another way to arrive at the same definition is to ask what logarithmic base

gives that the derivative of $\log_e(x)$ is

. We denote $\log_e(x)$ by $\ln(x)$ .

Numerically, is a transcendental number (a type of irrational number ^3.5), so its decimal expansion never repeats. The initial decimal expansion of is given by^3.6

$\displaystyle e = 2.7182818284590452353602874713526624977572470937\ldots\,.$

Any number of digits can be computed from the formula $(1+\delta)^{1/\delta}$ by making $\delta$ sufficiently small.

e^(j theta)

We've now defined for any positive real number and any complex number . Setting and $z=j\theta$ gives us the special case we need for Euler's identity. Since is its own derivative, the Taylor series expansion for is one of the simplest imaginable infinite series:

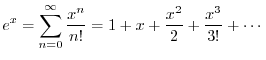
$\displaystyle e^x = \sum_{n=0}^\infty \frac{x^n}{n!} = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \cdots$

The simplicity comes about because $f^{(n)}(0)=1$ for all

and because we chose to expand about the point

. We of course define

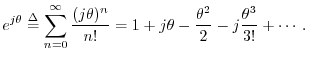
$\displaystyle e^{j\theta} \isdef \sum_{n=0}^\infty \frac{(j\theta)^n}{n!} = 1 + j\theta - \frac{\theta^2}{2} - j\frac{\theta^3}{3!} + \cdots \,.$

Note that all even order terms are real while all odd order terms are imaginary. Separating out the real and imaginary parts gives

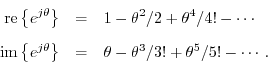
$\begin{eqnarray*} \mbox{re}\left\{e^{j\theta}\right\} &=& 1 - \theta^2/2 + \thet... ...heta}\right\} &=& \theta - \theta^3/3! + \theta^5/5! - \cdots\,. \end{eqnarray*}$

Comparing the Maclaurin expansion for $e^{j\theta }$ with that of $\cos(\theta)$ and $\sin(\theta)$ proves Euler's identity. Recall from introductory calculus that

$\begin{eqnarray*} \frac{d}{d\theta}\cos(\theta) &=& -\sin(\theta) \\ [5pt] \frac{d}{d\theta}\sin(\theta) &=& \cos(\theta) \end{eqnarray*}$

so that

$\begin{eqnarray*} \left.\frac{d^n}{d\theta^n}\cos(\theta)\right\vert _{\theta=0}... ...} \\ [5pt] 0, & n\;\mbox{\small even}. \\ \end{array} \right. \end{eqnarray*}$

Plugging into the general Maclaurin series gives

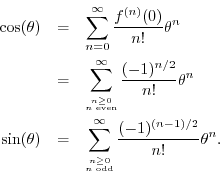
$\begin{eqnarray*} \cos(\theta) &=& \sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}\theta... ...mbox{\tiny$n$\ odd}}}^\infty \frac{(-1)^{(n-1)/2}}{n!} \theta^n. \end{eqnarray*}$

Separating the Maclaurin expansion for $e^{j\theta }$ into its even and odd terms (real and imaginary parts) gives

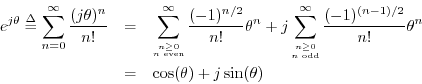
$\begin{eqnarray*} e^{j\theta} \isdef \sum_{n=0}^\infty \frac{(j\theta)^n}{n!} &... ...-1)^{(n-1)/2}}{n!} \theta^n\\ &=& \cos(\theta) + j\sin(\theta) \end{eqnarray*}$

thus proving Euler's identity.

Back to Mth Roots

As mentioned in §3.4, there are different numbers which satisfy when is a positive integer. That is, the th root of , which is written as $a^{1/M}$ , is not unique--there are of them. How do we find them all? The answer is to consider complex numbers in polar form. By Euler's Identity, which we just proved, any number, real or complex, can be written in polar form as

$\displaystyle z = r e^{j\theta}$

where $r\geq 0$ and $\theta\in[-\pi,\pi)$ are real numbers. Since, by Euler's identity, $e^{j2\pi k}=\cos(2\pi k)+j\sin(2\pi k)=1$ for every integer

, we also have

$\displaystyle z = r e^{j\theta} e^{j2\pi k}.$

Taking the

th root gives

$\displaystyle z^{\frac{1}{M}} = \left(r e^{j\theta} e^{j2\pi k}\right)^{\frac{... ...rac{k}{M}} = r^{\frac{1}{M}} e^{j\frac{\theta+2\pi k}{M}}, \quad k\in {\bf Z}.$

There are

different results obtainable using different values of

, e.g., $k=0,1,2,\dots,M-1$ . When

, we get the same thing as when

. When

, we get the same thing as when

, and so on, so there are only

distinct cases. Thus, we may define the

th-root of $z=r e^{j\theta}$ as

$\displaystyle r^{\frac{1}{M}} e^{j\frac{\theta+2\pi k}{M}}, \quad k=0,1,2,\dots,M-1.$

These are the

th-roots of the complex number $z=r e^{j\theta}$ .

Roots of Unity

Since $e^{j2\pi k}=1$ for every integer , we can write

$\displaystyle 1^{k/M} = e^{j2\pi k/M}, \quad k=0,1,2,3,\dots,M-1.$

These are the th roots of unity. The special case

is called a primitive th root of unity, since integer powers of it give all of the others:

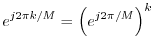
$\displaystyle e^{j2\pi k/M} = \left(e^{j2\pi/M}\right)^k$

The

th roots of unity are so frequently used that they are often given a special notation in the signal processing literature:

$\displaystyle W_M^k \isdef e^{j2\pi k/M}, \qquad k=0,1,2,\dots,M-1,$

where

denotes a primitive

th root of unity.^3.7 We may also call

a generator of the mathematical group consisting of the

th roots of unity and their products.

We will learn later that the th roots of unity are used to generate all the sinusoids used by the length- DFT and its inverse. The th complex sinusoid used in a DFT of length is given by

$\displaystyle W_N^{kn} = e^{j2\pi k n/N} \isdef e^{j\omega_k t_n} = \cos(\omega_k t_n) + j \sin(\omega_k t_n), \quad n=0,1,2,\dots,N-1,$

where $\omega_k \isdef 2\pi k/NT$ , $t_n \isdef nT$ , and

is the sampling interval in seconds.

Direct Proof of De Moivre's Theorem

In §2.10, De Moivre's theorem was introduced as a consequence of Euler's identity:

$\displaystyle \zbox {\left[\cos(\theta) + j \sin(\theta)\right] ^n = \cos(n\theta) + j \sin(n\theta), \qquad\hbox{for all $n\in{\bf R}$}}$

To provide some further insight into the ``mechanics'' of Euler's identity, we'll provide here a direct proof of De Moivre's theorem for integer

using mathematical induction and elementary trigonometric identities.

Proof: To establish the ``basis'' of our mathematical induction proof, we may simply observe that De Moivre's theorem is trivially true for . Now assume that De Moivre's theorem is true for some positive integer . Then we must show that this implies it is also true for , i.e.,

$\displaystyle \left[\cos(\theta) + j \sin(\theta)\right] ^{n+1} = \cos[(n+1)\theta] + j \sin[(n+1)\theta]. \protect$

(3.2)

Since it is true by hypothesis that

$\displaystyle \left[\cos(\theta) + j \sin(\theta)\right] ^n = \cos(n\theta) + j \sin(n\theta),$

multiplying both sides by $[\cos(\theta) + j \sin(\theta)]$ yields

$\displaystyle \left[\cos(\theta) + j \sin(\theta)\right] ^{n+1}$	$\displaystyle =$	$\displaystyle \left[\cos(n\theta) + j \sin(n\theta)\right] \cdot \left[\cos(\theta) + j \sin(\theta)\right]$
	$\displaystyle =$	$\displaystyle \qquad\! \left[\cos(n\theta)\cos(\theta) -\sin(n\theta)\sin(\theta)\right]$
		$\displaystyle \,+\, j \left[\sin(n\theta)\cos(\theta)+\cos(n\theta)\sin(\theta)\right]. \protect$	(3.3)

From trigonometry, we have the following sum-of-angle identities:

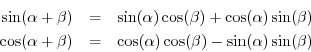
$\begin{eqnarray*} \sin(\alpha+\beta) &=& \sin(\alpha)\cos(\beta) + \cos(\alpha)\... ...pha+\beta) &=& \cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta) \end{eqnarray*}$

These identities can be proved using only arguments from classical geometry.^3.8Applying these to the right-hand side of Eq. $\,$ (3.3), with $\alpha=n\theta$ and $\beta=\theta$ , gives Eq. $\,$ (3.2), and so the induction step is proved. $\Box$

De Moivre's theorem establishes that integer powers of $[\cos(\theta) + j \sin(\theta)]$ lie on a circle of radius 1 (since $\cos^2(\phi)+\sin^2(\phi)=1$ , for all $\phi\in[-\pi,\pi]$ ). It therefore can be used to determine all of the th roots of unity (see §3.12 above). However, no definition of emerges readily from De Moivre's theorem, nor does it establish a definition for imaginary exponents (which we defined using Taylor series expansion in §3.7 above).