DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

High-Accuracy Piano-String Modeling

In [265,266], an extension of the mass-spring model of [391] was presented for the purpose of high-accuracy modeling of nonlinear piano strings struck by a hammer model such as described in §9.3.2. This section provides a brief overview.

Figure 9.25: Mass-spring model in 3D space.
\includegraphics[width=0.35\twidth]{eps/massspringmass}

Figure 9.25 shows a mass-spring model in 3D space. From Hooke's Law (§B.1.3), we have

$\displaystyle \vert\vert\,\underline{f}_1\,\vert\vert \eqsp k\cdot\vert l_1-l_0\vert \eqsp \vert\vert\,\underline{f}_1\,\vert\vert $

where $ l_0$ denotes the rest-length of the spring $ k$, and $ \vert\vert\,\underline{f}_i\,\vert\vert $ denotes the vector norm (length) of the 3D vector $ \underline{f}_i\in{\bf R}^3$ [451]. The vector equation of motion for mass 1 is given by Newton's second law $ f=ma$:

\begin{eqnarray*} m_1\, \underline{{\ddot x}}_1 \eqsp \underline{f}_1 &=& k\cdo... ...,\right\Vert}\right]\left(\underline{x}_2-\underline{x}_1\right) \end{eqnarray*}

and similarly for mass 2, where $ \underline{x}_i\in{\bf R}^3$ is the vector position of mass $ i$ in 3D space.

Generalizing to a chain of masses and spring is shown in Fig.9.26. Mass-spring chains--also called beaded strings--have been analyzed in numerous textbooks (e.g., [295,318]), and numerical software simulation is described in [391].

Figure 9.26: Mass-spring string model
\includegraphics[width=0.8\twidth]{eps/massspringstring}

The force on the $ i$th mass can be expressed as

$\displaystyle \underline{f}_i$ $\displaystyle =$ $\displaystyle \alpha_i\cdot\left(\underline{x}_{i+1}-\underline{x}_i\right) + \alpha_{i-1}\cdot\left(\underline{x}_{i-1}-\underline{x}_i\right)$  
  $\displaystyle =$ $\displaystyle \alpha_{i-1}\,\underline{x}_{i-1} - (\alpha_{i-1}+\alpha_i)\,\underline{x}_i + \alpha_i\,\underline{x}_{i+1} \protect$ (10.34)

where

$\displaystyle \alpha_i \isdefs k\cdot \left[1-\frac{l_0}{\left\Vert\,\underline{x}_{i+1}-\underline{x}_i\,\right\Vert}\right]. $

A Stiff Mass-Spring String Model

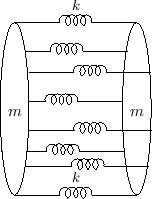
Following the classical derivation of the stiff-string wave equation [317,144], an obvious way to introduce stiffness in the mass-spring chain is to use a bundle of mass-spring chains to form a kind of ``lumped stranded cable''. One section of such a model is shown in Fig.9.27. Each mass is now modeled as a 2D mass disk. Complicated rotational dynamics can be avoided by assuming no torsional waves (no ``twisting'' motion) (§B.4.20).

Figure 9.27: Adding bending stiffness to the mass-spring string model.
\includegraphics{eps/massspringsmass}

A three-spring-per-mass model is shown in Fig.9.28 [266]. The spring positions alternate between angles $ (0,2\pi/3,4\pi/3)$, say, on one side of a mass disk and $ (\pi/3,\pi,5\pi/3)$ on the other side in order to provide effectively six spring-connection points around the mass disk for only three connecting springs per section. This improves isotropy of the string model with respect to bending direction.

Figure 9.28: Stiff mass-spring chain with alternating three-spring placement.
\includegraphics[width=0.8\twidth]{eps/masssprings3circ}

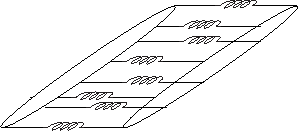
A problem with the simple mass-spring-chain-bundle is that there is no resistance whatsoever to shear deformation, as is clear from Fig.9.29. To rectify this problem (which does not arise due implicit assumptions when classically deriving the stiff-string wave equation), diagonal springs can be added to the model, as shown in Fig.[*].

Figure 9.29: Illustration of the need for shear stiffness in the model.
\includegraphics{eps/massspringsshearedai}

Figure: Geometry of added shear springs.
\includegraphics[width=0.4\twidth]{eps/masssprings3shear}
In the simulation results reported in [266], the spring-constants of the shear springs were chosen so that their stiffness in the longitudinal direction would equal that of the longitudinal springs.

Nonlinear Piano-String Equations of Motion in State-Space Form

For the flexible (non-stiff) mass-spring string, referring to Fig.9.26 and Eq.$ \,$(9.34), we have the following equations of motion:

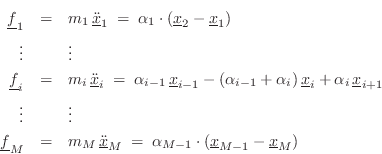
\begin{eqnarray*} \underline{f}_1 &=& m_1 \,\underline{{\ddot x}}_1 \eqsp \alpha... ...M \eqsp \alpha_{M-1}\cdot(\underline{x}_{M-1} - \underline{x}_M) \end{eqnarray*}

or, in $ 3M\times1$ vector form,

$\displaystyle \underline{F}\eqsp \mathbf{M}\, \ddot{\underline{X}} \eqsp \mathbf{A}\, \underline{X}. $

Here the string terminations (bridge and agraffe) are modeled simply as very large masses $ m_1$ and $ m_M$.

Finite Difference Implementation

Digitizing $ \underline{{\ddot x}}_i(t)$ via the centered second-order difference [Eq.$ \,$(7.5)]

$\displaystyle \underline{{\ddot x}}_n\isdefs \underline{x}_{n+1} - 2\underline{x}_n + \underline{x}_{n-1} $

we obtain the following explicit finite-difference scheme (§D.1):

$\displaystyle \underline{X}_{n+1} \eqsp \left[2\mathbf{I}+ \mathbf{M}^{-1}\mathbf{A}\right]\underline{X}_n - \underline{X}_{n-1} + B\uv_n, $

where $ \uv_n$ is the external input vector for exciting the string (driving three adjacent masses in simulations to date).

Note that requiring three adjacent spatial string samples to be in contact with the piano hammer during the attack (which helps to suppress aliasing of spatial frequencies on the string during the attack) implies a sampling rate in the vicinity of 6 megahertz [265]. Thus, the model is expensive to compute! However, results to date show a high degree of accuracy, as desired. In particular, the stretching of the partial overtones in the stiff-string model of Fig.[*] has been measured to be highly accurate despite using only three spring attachment points on one side of each mass disk [265].

See [53] for alternative finite-difference formulations that better preserve physical energy and have other nice properties worth considering.

Next Section:
Commuted Piano Synthesis
Previous Section:
Nonlinear Piano Strings