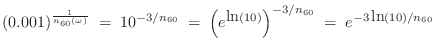Achieving Desired Reverberation Times

Free Books Physical Audio Signal Processing

A lossless prototype reverberator, as in Fig.3.10 when , has all of its poles on the unit circle in the plane, and its reverberation time is infinity. To set the reverberation time to a desired value, we need to move the poles slightly inside the unit circle. Furthermore, due to air absorption (§2.3,§B.7.15), we want the high-frequency poles to be more damped than the low-frequency poles [314]. As discussed in §2.3, this type of transformation can be obtained using the substitution

$\displaystyle z^{-1}\leftarrow G(z)z^{-1}, \protect$

(4.5)

where

denotes the filtering per sample in the propagation medium (a lowpass filter with gain not exceeding 1 at all frequencies).^4.14Thus, to set the FDN reverberation time to $t_{60}(\omega)\isdeftext n_{60}(\omega)T$ at frequency $\omega$ , we want propagation through $n_{60}$ samples to result in attenuation by

dB, i.e.,

$\displaystyle \left[G(e^{j\omega T})\right]^{n_{60}(\omega)} \eqsp 0.001. \protect$

(4.6)

Solving for

, the propagation attenuation per-sample, gives

$\displaystyle G(e^{j\omega T})$	$\displaystyle =\!$	$\displaystyle (0.001)^{\frac{1}{n_{60}(\omega)}} \eqsp 10^{-3/n_{60}} \eqsp \left(e^{\mbox{ln}(10)}\right)^{-3/n_{60}} \eqsp e^{-3\,\mbox{ln}(10)/n_{60}}$
	$\displaystyle =\!$	$\displaystyle e^{-T/\tau(\omega)} \protect$	(4.7)

The last form comes from $t_{60}=3$ ln $(10)\tau\approx 6.91\tau$ , where $\tau$ denotes the time constant of decay (time to decay by

) [451], i.e.,

$\displaystyle e^{-t_{60}/\tau}=0.001 \;\;\Leftrightarrow\;\; t_{60}\eqsp -3$ ln $\displaystyle (10)\tau. \protect$

(4.8)

Series expanding $e^{-T/\tau(\omega)}$ and assuming $n_{60}(\omega)\gg 7$ samples ( $\tau(\omega)\gg T$ seconds) provides the practically useful approximation

$\begin{eqnarray*} e^{-T/\tau(\omega)} &\!=\!& 1 - \frac{T}{\tau(\omega)} + \frac... ... \frac{3\mbox{ln}(10)}{n_{60}} \approxs 1 - \frac{6.91}{n_{60}}. \end{eqnarray*}$

Conformal Map Interpretation of Damping Substitution

The relation $G(e^{j\omega T})\approx e^{-T/\tau(\omega)}$ [Eq. $\,$ (3.7)] can be written down directly from $z^{-1}\leftarrow G(z)z^{-1}$ [Eq. $\,$ (3.5)] by interpreting Eq. $\,$ (3.5) as an approximate conformal map [326] which takes each pole $p_k=e^{j\omega_kT}$ , say, from the unit circle to the point $p'_k\approx G(e^{j\omega_kT})e^{-j\omega_kT}$ . Thus, the new pole radius is approximately $\vert p'_k\vert\approx\vert G(e^{j\omega_kT})\vert$ , where the approximation is valid when is approximately constant between the new pole location and the unit circle. To see this, consider the partial fraction expansion [449] of a proper th-order lossless transfer function mapped to $H'(z)\isdeftext H[z/G(z)]$ :

$\displaystyle H'(z) = \sum_{k=1}^N \frac{r_k}{1-p_kG(z)z^{-1}} = \sum_{k=1}^N r_k\left[1+p_kG(z)z^{-1}+p_k^2G^2(z)z^{-2}+\cdots\right],$

where $p_k=\exp(j\omega_k T)$ denotes the

th original pole on the unit circle. Then

has a pole at

, which must be solved iteratively for

, in general, since

can be a complicated function of

. However, if $G(z'_k)\approx G(p_k)$ , which is typically true when damping digital waveguides for music applications, then $z'_k\approx p_kG(p_k)=G[\exp(j\omega_k T)]\exp(j\omega_k T)$ . In other words, we can think of the pole

as moving from $\exp(j\omega_k T)$ to near $G[\exp(j\omega_k T)]\exp(j\omega_k T)$ , provided it doesn't move too far compared with the near-constant behavior of

. Another way to say it is that we need

to be approximately the same at the new pole location and its initial location on the unit circle in the lossless prototype.

Happily, while we may not know precisely where our poles have moved as a result of introducing the per-sample damping filter , the relation $G^{n_{60}(\omega)}(e^{j\omega T})=0.001$ [Eq. $\,$ (3.6)] remains exact at every frequency by construction, as it is based only on the physical interpretation of each unit delay as a propagation delay for a plane wave across one sampling interval , during which (zero-phase) filtering by is assumed (§2.3). More generally, we can design minimum-phase filters for which $\vert G^{n_{60}(\omega)}(e^{j\omega T})\vert=0.001$ , and neglect the resulting phase dispersion.

In summary, we see that replacing $z^{-1}$ by $G(z)z^{-1}$ everywhere in the FDN lossless prototype (or any lossless LTI system for that matter) serves to move its poles away from the unit circle in the plane onto some contour inside the unit circle that provides the desired decay time at each frequency.

A general design guideline for artificial reverberation applications [217] is that all pole radii in the reverberator should vary smoothly with frequency. This translates to having a smooth frequency response. To see why this is desired, consider momentarily the frequency-independent case in which we desire the same reverberation time at all frequencies (Fig.3.10 with real $g_i\le 1$ , as drawn). In this case, it is ideal for all of the poles to have this decay time. Otherwise, the late decay of the impulse response will be dominated by the poles having the largest magnitude, and it will be ``thinner'' than it was at the beginning of the response when all poles were contributing to the output. Only when all poles have the same magnitude will the late response maintain the same modal density throughout the decay.

Damping Filters for Reverberation Delay Lines

In an FDN, such as the one shown in Fig.3.10, delays $z^{-1}$ appear in long delay-line chains $z^{-M_i}$ . Therefore, the filter needed at the output (or input) of the th delay line is $G^{M_i}(z)$ (replace by $G^{M_i}(z)$ in Fig.3.10).^4.15 However, because $G(e^{j\omega T})$ is so close to in magnitude, and because it varies so weakly across the frequency axis, we can design a much lower-order filter $H_i(z)\approx G^{M_i}(z)$ that provides the desired attenuation versus frequency to within psychoacoustic resolution. In fact, perfectly nice reverberators can be designed in which is merely first order for each [314,217].