Perceptual Aspects of Reverberation
Artificial reverberation is an unusually interesting signal processing problem because, as discussed in the previous sections, the ``obvious'' methods based on physical modeling or input-output modeling are too expensive computationally for most applications. This leads to the question of what are the perceptually important aspects of reverberation, and how can these be provided by efficient computational structures.
Perception of Echo Density and Mode Density
The reverberation problem can be greatly simplified without
sacrificing perceptual quality. For example, it can be shown4.3that for typical rooms, the echo density increases as ![]() , where
, where ![]() is time. Therefore, beyond some time, the echo density is so great
that it can be modeled as some uniformly sampled stochastic process
without loss of perceptual fidelity. In particular, there is no need
to explicitly compute multiple echoes per sample of sound.
For smoothly decaying late reverb (the desired kind), an
appropriate random process sampled at the audio sampling rate will
sound equivalent perceptually.
is time. Therefore, beyond some time, the echo density is so great
that it can be modeled as some uniformly sampled stochastic process
without loss of perceptual fidelity. In particular, there is no need
to explicitly compute multiple echoes per sample of sound.
For smoothly decaying late reverb (the desired kind), an
appropriate random process sampled at the audio sampling rate will
sound equivalent perceptually.
Similarly, it can be shown4.4that the number of resonant modes in any given frequency band increases as frequency squared, so that above some frequency, the modes are so dense that they are perceptually equivalent to a random frequency response generated according to some statistics. In particular, there is no need to explicitly implement resonances so densely packed that the ear cannot hear them all.
In summary, we see that, based on limits of perception, the impulse response of a reverberant room can be divided into two segments. The first segment, called the early reflections, consists of the relatively sparse first echoes in the impulse response. The remainder, called the late reverberation, is so densely populated with echoes that it is best to characterize the response statistically in some way. Section 3.3 discusses methods for simulating early reflections in the reverberation impulse response.
Similarly, the frequency response of a reverberant room can be divided into two segments. The low-frequency interval consists of a relatively sparse distribution of resonant modes, while at higher frequencies the modes are packed so densely that they are best characterized statistically as a random frequency response with certain (regular) statistical properties. Section 3.4 describes methods for synthesizing hiqh quality late reverberation.
Perceptual Metrics for Ideal Reverberation
Some desirable controls for an artificial reverberator include [218]
-
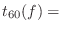 desired reverberation time at each frequency
desired reverberation time at each frequency 
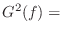 signal power gain at each frequency
signal power gain at each frequency
 ``clarity'' = ratio of impulse-response energy in early reflections to that in the late reverb
``clarity'' = ratio of impulse-response energy in early reflections to that in the late reverb
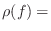 interaural correlation coefficient at left and right ears
interaural correlation coefficient at left and right ears
The time to decay 60 dB (![]() ) is a classical objective parameter
used as a measure of perceived reverberation time. Classically,
) is a classical objective parameter
used as a measure of perceived reverberation time. Classically,
![]() was measured for the whole response. More recently
[216], it has become more common to design for a given
was measured for the whole response. More recently
[216], it has become more common to design for a given ![]() at more
than one frequency, e.g., one for low frequencies, another for high
frequencies, and interpolated values at intermediate frequencies.
Perceptual studies indicate that reverberation time should be
independently adjustable in at least three frequency bands
[217].
at more
than one frequency, e.g., one for low frequencies, another for high
frequencies, and interpolated values at intermediate frequencies.
Perceptual studies indicate that reverberation time should be
independently adjustable in at least three frequency bands
[217].
Energy Decay Curve
For measuring and defining reverberation time ![]() , Schroeder
introduced the so-called
energy decay curve (EDC) which is the tail integral of the squared impulse
response at time
, Schroeder
introduced the so-called
energy decay curve (EDC) which is the tail integral of the squared impulse
response at time ![]() :
:
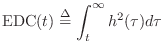
Energy Decay Relief
The energy decay relief (EDR) is a time-frequency distribution which generalizes the EDC to multiple frequency bands [215]:
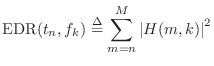
Thus,
![]() is the total amount of signal energy remaining
in the reverberator's impulse response at time
is the total amount of signal energy remaining
in the reverberator's impulse response at time ![]() in a frequency band centered
about
in a frequency band centered
about
![]() Hz, where
Hz, where ![]() denotes the FFT length.
denotes the FFT length.
The EDR of a violin-body impulse response is shown in Fig.3.2. For better correspondence with audio perception, the frequency axis is warped to the Bark frequency scale [459], and energy is summed within each Bark band (one critical band of hearing equals one Bark). A violin body can be regarded as a very small reverberant room, with correspondingly ``magnified'' spectral structure relative to reverberant rooms.
The EDR of the Boston Symphony Hall is displayed in [153, p. 96].
The EDR is used to measure partial overtone dampings from recordings of a vibrating string in §6.11.5.
Next Section:
Early Reflections
Previous Section:
The Reverberation Problem








![\includegraphics[width=\twidth]{eps/bodyBEDR}](http://www.dsprelated.com/josimages_new/pasp/img693.png)











