Free Books
   Free Books    Physical Audio Signal Processing  

Power-Normalized Waveguide Filters

Above, we adopted the convention that the time variation of the wave impedance did not alter the traveling force waves $ f^\pm _i$. In this case, the power represented by a traveling force wave is modulated by the changing wave impedance as it propagates. The signal power becomes inversely proportional to wave impedance:

$\displaystyle {\cal I}_i(t,x) = {\cal I}^{+}_i(t,x)+{\cal I}^{-}_i(t,x) = \frac{[f^{{+}}_i(t,x)]^2-[f^{{-}}_i(t,x)]^2}{R_i(t)} $

In some applications (such as time-varying waveguide reverberation [430]), it may be preferable to compensate for the power modulation so that changes in the wave impedances of the waveguides do not affect the power of the signals propagating within.

In [432,433], three methods are discussed for making signal power invariant with respect to time-varying branch impedances:

  1. The normalized waveguide scheme compensates for power modulation by scaling the signals leaving the delays so as to give them the same power coming out as they had going in. It requires two additional scaling multipliers per waveguide junction.

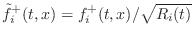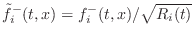  2. The normalized wave approach [297] propagates rms-normalized waves in the waveguide. In this case, each delay-line contains $ \tilde{f}^{+}_i(t,x) = f^{{+}}_i(t,x)/\sqrt{R_i(t)}$ and $ \tilde{f}^{-}_i(t,x) = f^{{-}}_i(t,x)/\sqrt{R_i(t)}$. In this case, the power stored in the delays does not change when the wave impedance changes. This is the basis of the normalized ladder filter (NLF) [174,297]. Unfortunately, four multiplications are obtained at each scattering junction.

  3. The transformer-normalized waveguide approach changes the wave impedance at the output of the delay back to what it was at the time it entered the delay using a ``transformer'' (defined in §C.16).

The transformer-normalized DWF junction is shown in Fig.C.27 [432]. As derived in §C.16, the transformer ``turns ratio'' $ g_i$ is given by

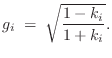
$\displaystyle g_i \eqsp \sqrt{\frac{1-k_i}{1+k_i}}. $

We can now modulate a single scattering junction, even in arbitrary network topologies, by inserting a transformer immediately to the left or right of the junction. Conceptually, the wave impedance is not changed over the delay-line portion of the waveguide section; instead, it is changed to the new time-varying value just before (or after) it meets the junction. When velocity is the wave variable, the coefficients $ g_i$ and $ g_i^{-1}$ in Fig.C.27 are swapped (or inverted).

Figure: Transformer-normalized one-multiply scattering junction, equivalent to the normalized scattering junction shown in Fig.C.22
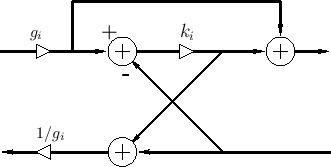\includegraphics{eps/tnscat}
.

So, as in the normalized waveguide case, for the price of two extra multiplies per section, we can implement time-varying digital filters which do not modulate stored signal energy. Moreover, transformers enable the scattering junctions to be varied independently, without having to propagate time-varying impedance ratios throughout the waveguide network.

It can be shown [433] that cascade waveguide chains built using transformer-normalized waveguides are equivalent to those using normalized-wave junctions. Thus, the transformer-normalized DWF in Fig.C.27 and the wave-normalized DWF in Fig.C.22 are equivalent. One simple proof is to start with a transformer (§C.16) and a Kelly-Lochbaum junction (§C.8.4), move the transformer scale factors inside the junction, combine terms, and arrive at Fig.C.22. One practical benefit of this equivalence is that the normalized ladder filter (NLF) can be implemented using only three multiplies and three additions instead of the usual four multiplies and two additions.

The transformer-normalized scattering junction is also the basis of the digital waveguide oscillator (§C.17).

Next Section:
Reflectance of an Impedance
Previous Section:
Conventional Ladder Filters