Examples in Matlab and Octave
This appendix contains some of the matlab scripts used in creating various figures in the text, as well as listings for the applications discussed in Chapter 10.
Matlab for Spectrum Analysis Windows
Blackman Window Example
Below is the Matlab script for creating Figures 2.6 and 2.7 in §2.5.4.
% Illustrate zero-phase zero-padding around a Blackman window % Analysis parameters: M = 31; % Window length N = 64; % FFT length (zero padding factor = N/M) Mo2 = (M-1)/2; % Shorthand dBCut = -100; % Clip dB at this level % Signal parameters (synthetic sinusoid): wxT = pi/exp(1);% Sinusoid frequency in rad/sample A = 1; % Sinusoid amplitude phix = pi/3; % Sinusoid phase % Compute the signal x: n = [0:N-1]; % time indices for sinusoid and FFT x = A * cos(wxT*n+phix); % a sinusoid % Compute a causal Blackman window: % w = blackman(M); % Matlab signal processing toolbox, or w = .42-.5*cos(2*pi*(0:M-1)/(M-1))+.08*cos(4*pi*(0:M-1)/(M-1)); % Apply the window: xw = w .* x(1:M); % Note that we have "skipped" the first Mo2 samples of x % since the center of the window is its proper time origin. % Form the zero-padded FFT input buffer. % Note how the negative-time portion goes on the right: xwzp = [xw(Mo2+1:M),zeros(1,N-M),xw(1:Mo2)]; wzp = [w(Mo2+1:M),zeros(1,N-M),w(1:Mo2)]; figure(1); subplot(1,1,1); % force a clear subplot(2,1,1); n = -Mo2:Mo2; % time axis for plot stem(n,xw,'ok'); % windowed data hold on; plot(n,w,':k'); % window plot(n,zeros(1,M),'-k'); % zero line title('Blackman Windowed Sinusoid'); xlabel('Time (samples)'); ylabel('Amplitude'); text(-8,1,'(a)'); hold off; subplot(2,1,2); n = 0:N-1; % FFT buffer time axis stem(n,xwzp,'ok'); hold on; plot(n,zeros(1,N),'-k'); % zero line plot(n,wzp,':k'); % window plot([N/2,N/2],[-1,1],'--k'); % dividing line text(N/4,0.2,'positive time'); text(N/2+N/8,0.2,'negative time'); xlabel('Time (samples)'); ylabel('Amplitude'); text(-8,1,'(b)'); saveplot('../eps/zpblackmanT.eps'); hold off; figure(2); subplot(1,1,1); % force a clear % Now show the window transform: Xwzp = fft(xwzp); % Blackman window transform spec = 20*log10(abs(Xwzp)); % Spectral magnitude in dB spec = spec - max(spec); % Normalize to 0 db max spec = max(spec,dBCut*ones(1,N)); % clip to dBCut dB subplot(2,1,1); fni = [0:1.0/N:1-1.0/N]; % Normalized frequency axis bins = [0:N-1]; % Bin axis Xwzpa = abs(Xwzp) stem(bins,Xwzpa,'ok'); hold on; plot([N/2,N/2],YLim,'--k'); % dividing line text(5,7,'positive frequencies'); text(45,7,'negative frequencies'); %zpblackmanplot3d axis([0,N-1,YLim]); xlabel('Frequency (bins))'); ylabel('Magnitude (linear)'); text(-8,8,'(a)'); % Replot interpreting upper bin numbers as (-) frequencies: subplot(2,1,2); sbins = bins - N/2; nh = N/2; sXwzpa = [Xwzpa(nh+1:N),Xwzpa(1:nh)]; % see also fftshift() %fninf = fni - 0.5; % Plot (-) freqs on the left %plot(fninf,sXwzpa,'-k'); axis([-0.5,0.5,dBCut,10]); grid; %plot(fni,Xwzpa,'-k'); grid; stem(sbins,abs(sXwzpa),'ok'); axis([-N/2,N/2-1,YLim]); hold on; plot([0,0],YLim,'--k'); % dividing line text(-20,7,'negative frequencies'); text(5,7,'positive frequencies'); xlabel('Frequency (bins))'); ylabel('Magnitude (linear)'); text(-48,8,'(b)'); saveplot('../eps/zpblackmanF.eps'); hold off;
Matlab listing: dpssw.m
function [w,A,V] = dpssw(M,Wc); % DPSSW - Compute Digital Prolate Spheroidal Sequence window of % length M, having cut-off frequency Wc in (0,pi). k = (1:M-1); s = sin(Wc*k)./ k; c0 = [Wc,s]; A = toeplitz(c0); [V,evals] = eig(A); % Only need the principal eigenvector [emax,imax] = max(abs(diag(evals))); w = V(:,imax); w = w / max(w);
Matlab for Finding Interpolated Spectral Peaks
Matlab listing: findpeaks.m
function [peakamps,peaklocs,peakwidths,resid] = ... findpeaks(data,npeaks,minwidth,maxwidth,minpeak,debug); %FINDPEAKS Find up to npeaks interpolated peaks in data. % % [peakamps,peaklocs,peakwidths,resid] = % findpeaks(data,npeaks,minwidth,maxwidth,minpeak,debug); % % finds up to npeaks interpolated peaks in real data. % A peak is rejected if its width is % less than minwidth samples wide(default=1), or % less than minpeak in magnitude (default=min(data)). % Quadratic interpolation is used for peak interpolation. % Left-over data with peaks removed is returned in resid. % Peaks are returned in order of decreasing amplitude. % They can be sorted in order of location as follows: % [peaklocs,sorter] = sort(peaklocs); % amps = zeros(size(peakamps)); % npeaks = length(peaklocs); % for col=1:npeaks, % amps(:,col) = peakamps(:,sorter(col)); % end; % They can be sorted in order of width as follows: % [peakwidths,sorter] = sort(peakwidths); % peakamps = peakamps(sorter); % peaklocs = peaklocs(sorter); len = length(data); if nargin<6, debug = 0; end; if nargin<5, minpeak = min(data); end; if nargin<4, maxwidth = 0; end; if nargin<3, minwidth = 1; end; if nargin<2, npeaks = len; end; peakamps = zeros(1,npeaks); peaklocs = zeros(1,npeaks); peakwidths = zeros(1,npeaks); if debug, peaksarr = 1.1*max(data)*ones(size(data)); end; if debug, orgdata = data; end; if debug, npeaks, end nrej = 0; pdebug=debug; ipeak=0; while ipeak<npeaks [ploc, pamp, pcurv] = maxr(data); if (pamp==minpeak), warning('findpeaks:min amp reached'); break; end plocq = round(ploc); ulim = min(len,plocq+1); camp = pamp; % % Follow peak down to determine its width % drange = max(data) - minpeak; % data dynamic range tol = drange * 0.01; dmin = camp; while ((ulim<len) & (data(ulim)<=dmin+tol)), camp = data(ulim); ulim = ulim + 1; if (camp<dmin), dmin=camp; end end; ulim = ulim - 1; lamp = camp; llim = max(1,plocq-1); camp = pamp; dmin = camp; while ((llim>1) & (data(llim)<=dmin+tol)), camp = data(llim); llim = llim - 1; if (camp<dmin), dmin=camp; end end; llim = llim + 1; uamp = camp; % % Remove the peak % data(llim:ulim) = min(lamp,uamp) * ones(1,ulim-llim+1); % % Reject peaks which are too narrow (indicated by zero loc and amp) % pwid = ulim - llim + 1; if ~(pwid < minwidth), ipeak = ipeak + 1; peaklocs(ipeak) = ploc; peakamps(ipeak) = pamp; peakwidths(ipeak) = - 1/pcurv; nrej = 0; if pdebug>1 peaksarr(plocq) = pamp; maxloc = min(len,2*round(max(peaklocs))); ttl = sprintf(... 'Peak %d = %0.2f at %0.2f, width %d',ipeak,pamp,ploc,pwid); if x == -1 pdebug = 0; end end else nrej = nrej + 1; if (nrej >= 10), warning('*** findpeaks: giving up (10 rejected peaks in a row)'); break; end; end; end; if (ipeak<npeaks), warning(sprintf(... '*** peaks.m: only %d peaks found instead of %d',ipeak,npeaks)); peakamps = peakamps(1:ipeak); peaklocs = peaklocs(1:ipeak); peakwidths = peakwidths(1:ipeak); end; resid = data;
Matlab listing: maxr.m
function [xi,yi,hc] = maxr(a) %MAXR Find interpolated maximizer(s) and max value(s) % for (each column of) a. % % [xi,yi,hc] = maxr(a) % % Calls max() followed by qint() for quadratic interpolation. % [m,n] = size(a); if m==1, a=a'; t=m; m=n; n=t; end; [y,x] = max(a); xi=x; % vector of maximizer locations, one per col of a yi=y; % vector of maximum values, one per column of a if nargout>2, hc = zeros(1,n); end for j=1:n, % loop over columns if x(j)>1, % only support interior maxima if x(j)<m, [xdelta,yij,cj] = qint(a(x(j)-1,j),y(j),a(x(j)+1,j)); xi(j) = x(j) + xdelta; if nargout>2, hc(j) = cj; end if (nargout>1), yi(j) = yij; end end; end; end;
Matlab listing: qint.m
function [p,y,a] = qint(ym1,y0,yp1) %QINT Quadratic interpolation of 3 uniformly spaced samples % % [p,y,a] = qint(ym1,y0,yp1) % % returns extremum-location p, height y, and half-curvature a % of a parabolic fit through three points. % The parabola is given by y(x) = a*(x-p)^2+b, % where y(-1)=ym1, y(0)=y0, y(1)=yp1. p = (yp1 - ym1)/(2*(2*y0 - yp1 - ym1)); if nargout>1 y = y0 - 0.25*(ym1-yp1)*p; end; if nargout>2 a = 0.5*(ym1 - 2*y0 + yp1); end;
Matlab listing: zpfmin.m
function [zpmin] = zpfmin(window,MT,freqBiasMax); % [zpmin] = zpfmin(window,MT,freqBiasMax) % returns the minimum zero-padding factor to achieve prescribed % tolerances in sinusoidal peak parameters measured using the QIFFT % method with the window. % % INPUTS: % window = 'rect', 'hamming', 'hann', or 'blackman' % MT = window length (seconds) % freqBiasMax = max frequency bias allowed in peak frequency (Hz) % ampBiasMax = max peak-magnitude bias allowed (relative fraction) % % If ampBiasMaxPct is not specified, amplitude bias is not considered. % % RETURNED: % zpmin = minimum zero-padding factor (1 means no zero padding) % % EXAMPLE % Assuming the window contains one cycle of a sinusoid whose % frequency f must be estimated to within 0.1% accuracy, we have % zpfmin('blackman',1/f,0.001*f) = 1.9 for min zero-padding factor. % Similarly, % 2 cycles under the Blackman window yields zpf > 1.5 % 4 cycles under the Blackman window yields zpf > 1.2 % 6 cycles under the Blackman window yields zpf > 1.02 % % Reference: % "Design Criteria for Simple Sinusoidal Parameter Estimation % based on Quadratic Interpolation of FFT Magnitude Peaks", by % Mototsugu Abe and Julius O. Smith, % Audio Engineering Society Convention preprint 6256", NY, 2004. %!test %! assert(zpfmin('blackman',1,0.001),2.3609,0.001); % disp(sprintf('%s window',window)); switch window case 'rect' c0 = 0.4467; r0 = -0.3218; c1 = 0.8560; r1 = -0.2366; case 'hamming' c0 = 0.2456; r0 = -0.3282; c1 = 0.4381; r1 = -0.2451; case 'hann' c0 = 0.2436; r0 = -0.3288; c1 = 0.4149; r1 = -0.2456; case 'blackman' c0 = 0.1868; r0 = -0.3307; c1 = 0.3156; r1 = -0.2475; otherwise error(sprintf('Window type %s unknown - say help zpfmin',window)); end zpmin = c0*(MT*freqBiasMax)^r0; if nargin>3 zpminamp = c1*(MT*freqBiasMax)^r1; zpmin = max(zpmin,zpminamp); end if strcmp(window,'rect') zpmin=max(1.7,zpmin); % See Abe & Smith 2004, Fig. 2 re. why this else zpmin=max(1,zpmin); end
Matlab listing: oboeanal.m
The following Matlab script illustrates use of the findpeaks function above to determine the pitch of an oboe tone (given the general location of the correct spectral peak) and configure a spectrum analysis using the rectangular, Hamming, and Blackman windows. This script was used to create Figures 3.16 through 3.18.
diary './dia/oboeanal.dia'; diary on; zpf = 5; % desired min zero-padding factor in all FFTs fn = '../wav/oboe.ff.C4B4.wav'; [x,fs,nbits] = wavread(fn); nx = length(x); dur = nx/fs; disp(sprintf(['Read %s, fs = %f, nbits = %d, ',... 'length = %d samples = %0.1f sec'],... fn,fs,nbits,nx,dur)); soundsc(x,fs); M = fs/10; % 100 ms window for pitch estimation N = 2^nextpow2(M*zpf) % zero pad Xzp = fft(x,N); figure(K-1); fmax = 500; % maximum freq in Hz kmax = fmax*N/fs; % maximum freq in bins prange = 1:kmax+1; Xdb = dbn(Xzp(prange)); % dB normalized to 0 max f = fs*[0:N-1]/N/1000; % frequency axis in kHz plot(f(prange),Xdb); ylabel('Magnitude (dB)'); xlabel('Normalized Frequency (cycles/sample)'); [amps,bins] = findpeaks(Xdb,1); k0 = bins(1)-1; f0 = k0*fs/N; nP = fs/f0; % samples per period (used below) disp(sprintf('Estimated pitch = %f Hz',f0)); % Test pitch estimate: pause(ceil(dur)); % let previous sound finish T = 1/fs; t = 0:T:dur; y = sawtooth(2*pi*f0*t); sound(y,fs) winnames={'none','boxcar','none','hamming','none','blackman'}; % Configure window analysis for K=[2 4 6] wintype = winnames{K}; M = ceil(K*nP); % min Blackman length cmd = sprintf('w = %s(M);',wintype); eval(cmd); Nw = 2^nextpow2(M*zpf) % zero pad xw = x(1:M) .* w; Xwzp = fft(xw,Nw); %fmax = 5*f0; % maximum freq in Hz fmax = fs/4; kmax = fmax*Nw/fs; % maximum freq in bins prange = 1:kmax+1; Xwdb = dbn(Xwzp(prange)); % dB normalized to 0 max figure(K); subplot(2,1,1); plot(xw,'-k'); axis tight; title(sprintf('Oboe data - %s window, K=%d',wintype,K)); ylabel('Amplitude'); xlabel('Time (samples)'); subplot(2,1,2); f = fs*[0:Nw-1]/Nw/1000; % frequency axis in kHz plot(f(prange),Xwdb,'-k'); grid on; axis([f(prange(1)) f(prange(end)) -90 0]); ylabel('Magnitude (dB)'); xlabel('Frequency (kHz)'); plotfile = sprintf('../eps/oboe%s.eps',wintype); saveplot(plotfile); end diary off;
Matlab for Computing Spectrograms
The Matlab Signal Processing Toolbox provides the command spectrogram for computing and displaying a spectrogram (and Octave has the command stft). As a side effect, it returns the complex STFT data in a matrix.
The myspectrogram function below illustrates computation of a spectrogram in matlab for purposes of basic spectrum analysis. It is compatible with the basic functionality of Matlab's spectrogram function, but does not implement all of its features.
We also include invmyspectrogram, which inverts a spectrogram to reproduce the corresponding time-domain signal. Finally, testmyspectrogram is included to illustrate their performance on test signal.
Matlab listing: myspectrogram.m
function X = myspectrogram(x,nfft,fs,window,noverlap,doplot,dbdown); %MYSPECTROGRAM Calculate spectrogram from signal. % B = MYSPECTROGRAM(A,NFFT,Fs,WINDOW,NOVERLAP) calculates the % spectrogram for the signal in vector A. % % NFFT is the FFT size used for each frame of A. It should be a % power of 2 for fastest computation of the spectrogram. % % Fs is the sampling frequency. Since all processing parameters are % in units of samples, Fs does not effect the spectrogram itself, % but it is used for axis scaling in the plot produced when % MYSPECTROGRAM is called with no output argument (see below). % % WINDOW is the length M window function applied, IN ZERO-PHASE % FORM, to each frame of A. M cannot exceed NFFT. For M<NFFT, % NFFT-M zeros are inserted in the FFT buffer (for interpolated % zero-phase processing). The window should be supplied in CAUSAL % FORM. % % NOVERLAP is the number of samples the sections of A overlap, if % nonnegative. If negative, -NOVERLAP is the "hop size", i.e., the % number of samples to advance successive windows. (The overlap is % the window length minus the hop size.) The hop size is called % NHOP below. NOVERLAP must be less than M. % % If doplot is nonzero, or if there is no output argument, the % spectrogram is displayed. % % When the spectrogram is displayed, it is ``clipped'' dbdown dB % below its maximum magnitude. The default clipping level is 100 % dB down. % % Thus, MYSPECTROGRAM splits the signal into overlapping segments of % length M, windows each segment with the length M WINDOW vector, in % zero-phase form, and forms the columns of B with their zero-padded, % length NFFT discrete Fourier transforms. % % With no output argument B, MYSPECTROGRAM plots the dB magnitude of % the spectrogram in the current figure, using % IMAGESC(T,F,20*log10(ABS(B))), AXIS XY, COLORMAP(JET) so the low % frequency content of the first portion of the signal is displayed % in the lower left corner of the axes. % % Each column of B contains an estimate of the short-term, % time-localized frequency content of the signal A. Time increases % linearly across the columns of B, from left to right. Frequency % increases linearly down the rows, starting at 0. % % If A is a length NX complex signal, B is returned as a complex % matrix with NFFT rows and % k = floor((NX-NOVERLAP)/(length(WINDOW)-NOVERLAP)) % = floor((NX-NOVERLAP)/NHOP) % columns. When A is real, only the NFFT/2+1 rows are needed when % NFFT even, and the first (NFFT+1)/2 rows are sufficient for % inversion when NFFT is odd. % % See also: Matlab's SPECTROGRAM and Octave's STFT function. % 02/04/02/jos: Created % 02/12/04/jos: Added dbdown % 07/23/08/jos: Changed name from SPECTROGRAM to MYSPECTROGRAM if nargin<7, dbdown=100; end if nargin<6, doplot=0; end if nargin<5, noverlap=256; end if nargin<4, window=hamming(512); end if nargin<3, fs=1; end if nargin<2, nfft=2048; end x = x(:); % make sure it's a column M = length(window); if (M<2) error(... 'myspectrogram: Expect complete window, not just its length'); end; if (M<2) error(... 'myspectrogram: Expect complete window, not just its length'); end; if length(x)<M % zero-pad to fill a window: x = [x;zeros(M-length(x),1)]; end; Modd = mod(M,2); % 0 if M even, 1 if odd Mo2 = (M-Modd)/2; w = window(:); % Make sure it's a column if noverlap<0 nhop = - noverlap; noverlap = M-nhop; else nhop = M-noverlap; end nx = length(x); %nframes = 1+floor((nx-noverlap)/nhop); nframes = 1+ceil(nx/nhop); X = zeros(nfft,nframes); % allocate output spectrogram zp = zeros(nfft-M,1); % zero-padding for each FFT xframe = zeros(M,1); xoff = 0 - Mo2; % input time offset = half a frame for m=1:nframes % M,Mo2,xoff,nhop if xoff<0 xframe(1:xoff+M) = x(1:xoff+M); % partial input data frame else if xoff+M > nx xframe = [x(xoff+1:nx);zeros(xoff+M-nx,1)]; else xframe = x(xoff+1:xoff+M); % input data frame end end xw = w .* xframe; % Apply window xwzp = [xw(Mo2+1:M);zp;xw(1:Mo2)]; X(:,m) = fft(xwzp); xoff = xoff + nhop; % advance input offset by hop size end if (nargout==0) | doplot t = (0:nframes-1)*nhop/fs; f = 0.001*(0:nfft-1)*fs/nfft; Xdb = 20*log10(abs(X)); Xmax = max(max(Xdb)); % Clip lower limit to -dbdown dB so nulls don't dominate: clipvals = [Xmax-dbdown,Xmax]; imagesc(t,f,Xdb,clipvals); % grid; axis('xy'); colormap(jet); xlabel('Time (sec)'); ylabel('Freq (kHz)'); end
Matlab listing: invmyspectrogram.m
function a = invmyspectrogram(b,hop) %INVMYSPECTROGRAM Resynthesize a signal from its spectrogram. % A = INVMYSPECTROGRAM(B,NHOP) % B = complex array of STFT values as generated by MYSPECTROGRAM. % The number of rows of B is taken to be the FFT size, NFFT. % INVMYSPECTROGRAM resynthesizes A by inverting each frame of the % FFT in B, and overlap-adding them to the output array A. % NHOP is the overlap-add offset between successive IFFT frames. % % See also: MYSPECTROGRAM [nfft,nframes] = size(b); No2 = nfft/2; % nfft assumed even a = zeros(1, nfft+(nframes-1)*hop); xoff = 0 - No2; % output time offset = half of FFT size for col = 1:nframes fftframe = b(:,col); xzp = ifft(fftframe); % xzp = real(xzp); % if signal known to be real x = [xzp(nfft-No2+1:nfft); xzp(1:No2)]; if xoff<0 % FFT's "negative-time indices" are out of range ix = 1:xoff+nfft; a(ix) = a(ix) + x(1-xoff:nfft)'; % partial frames out else ix = xoff+1:xoff+nfft; a(ix) = a(ix) + x'; % overlap-add reconstruction end xoff = xoff + hop; end
Matlab listing: testmyspectrogram.m
% testmyspectrogram.m (tested July 2008 in Octave 3.0) fs=22050; % sampling frequency D=1; % test signal duration in seconds L = ceil(fs*D)+1; % signal duration in samples n = 0:L-1; % discrete-time axis (samples) t = n/fs; % discrete-time axis (sec) %c = ones(1,L); % dc test (good first COLA check) c = chirp(t,0,D,fs/2); % sine sweep from 0 Hz to fs/2 Hz windur = 0.01; % window length in sec M = 2*round((windur*fs-1)/2); % win length in samples (even) %M = 2*round((windur*fs-1)/2)+1; % win length in samples (odd) Modd = mod(M,2); hop = (M-Modd)/2; if Modd w = 0.54 - 0.46 * cos(2*pi*(0:M-1)'/(M-1)); % causal Hamming window w(1)=w(1)/2; w(M)=w(M)/2; % modify for constant-overlap-add else w = 0.54 - 0.46 * cos(2*pi*(0:M-1)'/M); % causal Hamming window end w = w/(2*0.54); % scale for unity overlap-add nfft = 2^(3+nextpow2(M)); % For zero-phase processing, the signal should have at least % half a window of leading and trailing zeros zp = zeros(1,(M+Modd)/2); x = [zp,c,zp]; figure(1); clf; X = myspectrogram(x,nfft,fs,w,-hop,1); %or myspectrogram(x,nfft,fs,w,M-hop,1); title('Spectrogram of test signal'); % print -depsc 'testmyspectrogram.eps'; % write plot to disk %xh = invmyspectrogram(X,hop,8); xh = invmyspectrogram(X,hop); xh = real(xh); % imaginary part is round-off noise since x was real xmxh = x - xh(1:length(x)); % Have extra zeros at end of xh err=norm(xmxh)/norm(x); disp(sprintf('L2 norm of relative reconstruction error = %g',err)); % I observe 8E-16 for both odd and even win length cases - jos figure(2); clf; %n1 = round(L/8); n2 = n1+100; n1 = 1; n2 = n1+3000; pn = n1:n2; % plot indices %plot(n(pn),[x(pn)',xh(pn)']); %legend('original','resynthesized'); %title('Original and resynthesized test signal'); plot(n(pn),x(pn)-xh(pn)); title('Original minus resynthesized test signal'); figure(3); clf; Xh=myspectrogram(xh,nfft,fs,w,-hop,1); title('Spectrogram of resynthesized test signal');
Matlab for Unwrapping Spectral Phase
When spectral phase is processed, it is often necessary
to unwrap the phase to make it a ``continuous'' function.
Below is a simple matlab function for this purpose. It is based on
the assumption that phase jumps by more than ![]() radians must have
been ``wrapped''. That is, multiples of
radians must have
been ``wrapped''. That is, multiples of ![]() are added or
subtracted so that the phase changes by no more than
are added or
subtracted so that the phase changes by no more than ![]() from one
spectral bin to the next. Bin 0 (corresponding to dc) is arbitrarily
chosen as ``unwrapped'' and used as a starting point for the
unwrapping algorithm.
from one
spectral bin to the next. Bin 0 (corresponding to dc) is arbitrarily
chosen as ``unwrapped'' and used as a starting point for the
unwrapping algorithm.
Matlab listing: unwrap.m
function up = unwrap(p)
%UNWRAP unwrap phase
N = length(p);
up = zeros(size(p));
pm1 = p(1);
up(1) = pm1;
po = 0;
thr = pi - eps;
pi2 = 2*pi;
for i=2:N
cp = p(i) + po;
dp = cp-pm1;
pm1 = cp;
if dp>thr
while dp>thr
po = po - pi2
dp = dp - pi2;
end
end
if dp<-thr
while dp<-thr
po = po + pi2
dp = dp + pi2;
end
end
cp = p(i) + po;
pm1 = cp;
up(i) = cp;
end
Non-Parametric Frequency Warping
function [si] = specinterp(spec,indices); %SPECINTERP % [si] = specinterp(spec,indices); % % Returns spectrum sampled at indices (from 1). % Assumes a causal rectangular window was used. % The spec array should be the WHOLE spectrum, % not just 0 to half the sampling rate. % An "index" is a "bin number" + 1. % EXAMPLE: % N = 128; % x = sin(2*pi*0.1*[0:N-1]); % X = fft(x); % Xi = specinterp(X,[1:0.5:N]); % upsample by 2 % xi = ifft(x); % should now see 2x zero-padding N = length(spec); ibins = indices - 1; wki = ibins*2*pi/N; M = length(indices); si = zeros(1,M); wk = [0:N-1]*2*pi/N; for i=1:M index = indices(i); ri = round(index); if abs(index - ri) < 2*eps si(i) = spec(ri); else w = wki(i); % ideal interp kernel: wts = (1-exp(j*(wk-w)*N)) ./ (N*(1-exp(j*(wk-w)))); si(i) = sum(wts .* spec); end end |
Note that resampling a spectrum using the ideal interpolation kernel
requires
![]() operations, This computational burden can be
reduced in a number of ways:
operations, This computational burden can be
reduced in a number of ways:
- A window
 other than the rectangular window can be applied
to the data frame, so that
other than the rectangular window can be applied
to the data frame, so that
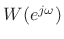 can be used as an interpolation
kernel in place of the aliased sinc function. If the window side lobes
are sufficiently small, they can be neglected. An example would be
can be used as an interpolation
kernel in place of the aliased sinc function. If the window side lobes
are sufficiently small, they can be neglected. An example would be
 set to a Hann window, with 50% overlap between frames, as
commonly used in the STFT.
set to a Hann window, with 50% overlap between frames, as
commonly used in the STFT.
- In pure frequency-warping applications, windows can be used for both analysis and reconstruction, as is done in apparently all perceptual audio coding methods such as MPEG [16,273]. For example, the square root of the Hann window can be applied to the analysis frame as well as the final overlap-add frame. This scheme has the advantage of tapering any discontinuities at the frame boundary more gracefully to zero, thus reducing the audibility of artifacts.
- Specially optimized narrow-support kernels can be designed by a number of methods [72,218]. If they are constrained to be nonnegative, their square root can be used twice like the Hann window in the previous point. Asymmetric factorizations are also possible when the kernel changes sign.
Fundamental Frequency Estimation
The f0est function requires findpeaks listed in §F.2.1. It also uses a trivial utility freqlabs defined at the end of the listing below. The blackman function (for the Blackman window) comes standard with Octave and requires the Signal Processing Toolbox in Matlab.
function [f0,fc] = f0est(sig,fs,framesize,npartials,minlevel,debug); %F0EST Estimate fundamental frequency F0 from spectral peaks % % [f0,fc] = f0est(sig,fs,framesize,npartials,minlevel); % % Computes fundamental frequency estimate f0 (Hz) and spectral cut-off % frequency fc (Hz) from spectral peaks for npartials partials in % signal sig. The frame size used in the fft is specified in % framesize which is rounded up to the next odd number if necessary. % The sampling rate is passed in fs (default = 1). Peaks are rejected % minlevel dB below the highest peak. fc is returned as the frequency % (Hz) of the highest partial. A Blackman window is used. sig = sig(:).'; % ensure row-vector len = length(sig); if (nargin<2), fs = 1; end; if (nargin<3), framesize = 512; end; if (nargin<5), minlevel = -60; % dB end; if (nargin<6), debug = 0; end; if (len < framesize), disp(sprintf('*** f0est: signal too short for fft (%d samples)',len)); framesize = len; end; if mod(framesize,2)==0, framesize = framesize - 1; disp(sprintf('f0est: framesize -> next odd number = %d',framesize)); end; minzpadfactor = 5; % min zero-padding factor (for accurate freqs) nfft = 2^nextpow2(framesize*minzpadfactor); nspec = nfft/2 + 1; [fkHz fxlab fylab] = freqlabs(nspec,fs); nzpad = nfft - framesize; padding = zeros(1,nzpad); zpadfactor = nfft/framesize; locscl = (fs/2) / nfft; % Converts bin to freq if (nargin<4), npartials = framesize/2; % i.e., no upper limit end; window = blackman(framesize)'; % Parameters established. % Compute FFT. minpeakwidth = zpadfactor*5; % 5 for generalized Blackman family maxpeakwidth = minpeakwidth*2; % reject too much modulation/interf. forigin = 1; frame = [window .* sig(forigin:forigin+framesize-1), padding]; if debug>1, plot(frame); title(sprintf('Signal Frame')); end; spec = fft(frame); specdb = db(spec(1:nspec)); minval = max(specdb) + minlevel; if debug, plot(fkHz,specdb); title('Signal Frame Spectrum'); xlabel(fxlab); ylabel(fylab); end; [peakamps peaklocs peakwidths] = ... findpeaks(specdb,npartials,minpeakwidth,maxpeakwidth,minval,debug); [peaklocs,sorter] = sort(peaklocs); amps = zeros(size(peakamps)); widths = zeros(size(peakamps)); npeaks = length(peaklocs); for col=1:npeaks, amps(:,col) = peakamps(:,sorter(col)); widths(:,col) = peakwidths(:,sorter(col)); end; freqs = (peaklocs - ones(size(peaklocs))) * fs / nfft; if npeaks>1, fspacings = diff(freqs); medianfspacing = median(fspacings); avgfspacing = mean(fspacings); else fspacings = freqs(1); medianfspacing = freqs(1); avgfspacing = freqs(1); end; f0a = medianfspacing; harmonic_numbers = round(freqs/f0a); subharms = find(harmonic_numbers < 0.75); msh = max(subharms); if msh > 0 % delete subharmonics, dc peak, etc. disp(sprintf(... '*** Tossing out the following %d peaks below F0',msh)); format bank; disp(' freqs amps widths:'); [freqs(1:msh)', amps(1:msh)', widths(1:msh)'] disp('*** PAUSING (RETURN to continue) ***'); pause; freqs = freqs(msh+1:npeaks); amps = amps(msh+1:npeaks); widths = widths(msh+1:npeaks); harmonic_numbers = harmonic_numbers(msh+1:npeaks); npeaks = npeaks - msh; end if debug, format bank; disp(' freqs amps widths:'); [freqs', amps', widths'] disp('partial frequency intervals:'); fspacings bar(freqs(1:end-1),fspacings-f0a); title('Partial Frequency Spacings minus fundamental'); ylabel('Frequency Spacing (Hz)'); xlabel('Frequency (Hz)'); disp('PAUSING - RETURN to continue'); pause; disp(sprintf('Median partial frequency interval = %f',medianfspacing)); disp(sprintf('Average partial frequency interval = %f',avgfspacing)); disp(sprintf('Fundamental frequency estimate = %f',f0a)); disp(sprintf('Harmonics versus peaks:')); [f0a*harmonic_numbers',freqs'] disp(sprintf('Relative deviation:')); disp(sprintf('Relative deviation (%%):')); f0a_error = 100*(freqs - f0a*harmonic_numbers)./freqs bar(freqs,f0a_error*1200); title('Relative Partial Frequency Deviations (measured - harmonic)'); ylabel('Cents'); xlabel('Frequency'); disp('PAUSING - RETURN to continue'); pause; disp(sprintf('Saved output format:')); nfreqs = length(freqs); [sprintf('partial_freqs = {%f',freqs(1)), ... sprintf(', %f',freqs(2:nfreqs)),sprintf('};')] [sprintf('partial_numbers = {%d',harmonic_numbers(1)),... sprintf(', %d',harmonic_numbers(2:nfreqs)),sprintf('};')] end; % % Optimize fit of f0 * harmonic_numbers to measured peak frequencies. % R = harmonic_numbers * harmonic_numbers'; P = harmonic_numbers * freqs'; f0 = R\P; if debug > 1, disp('Refined F0 estimate via harmonic regression:'); f0 disp('refined harmonics versus peaks:'); [f0*harmonic_numbers',freqs'] disp('relative deviation (%%):'); f0_error=100*(f0*harmonic_numbers-freqs)./freqs stem(f0_error); title('Relative Harmonic Deviation: Harmonic Minus Peak Over Peak'); end; fc = max(freqs); specdbc = max(specdb,minval); if debug, ttl = 'Signal Frame Spectrum with F0 and Cut-Off Marked'; clf; hold on; f = fkHz * 1000; plot(f,specdbc,'-k'); markline = [min(specdbc),max(specdbc)]; plot([f0 f0], markline); plot([fc fc], markline); title(ttl); xlabel(fxlab); ylabel(fylab); disp('PAUSING (CUTOFFS) - RETURN to continue'); pause; hold off; end; % ---------------------------------------------------------------- function [f,fxlab,fylab] = freqlabs(nspec,fs); %FREQLABS returns freq axis f (kHz), x label, and y label, given % max FFT bin number spec and sampling rate fs (in Hz) fxlab = 'Frequency (kHz)'; fylab = 'Amplitude (dB)'; f = (fs/2000)*[0:nspec-1]/nspec; % frequency axis for spectral plots
Test Program for F0 Estimation
The following test program generates a harmonic signal and uses f0est to determine the fundamental frequency, first with all harmonics present, and second with the fundamental suppressed by a notch filter.
% Tested using Octave 3.0.0, Aug 2008 clear all; f0 = 440; % true fundamental frequency n = 1:200; % time in samples fs = 10000; % sampling rate N = length(n); fund = sin(2*pi*f0*n/fs); % sine at fundamental frequency npartials = 7; sig = zeros(1,N); for k=1:npartials ampk = 1 / k^2; % give a natural roll-off sig = sig + ampk * sin(2*pi*k*f0*n/fs); end %rmsnoise = 0.01; rmsnoise = 0.0; sig = sig + rmsnoise * randn(1,N); % add some noise for realism framesize = N; minlevel = -60; % Lowest relative partial amplitude to accept % (-40 good with Hamming window family) % (-60 good with Blackman window family) debug = 0; f0 = f0est(sig,fs,framesize,npartials,minlevel,debug) % Trick to leave all internal f0est variables defined % (comment-out first line of f0est.m declaring the function): % nargin = 6; f0est; % Notch out fundamental and repeat: b1 = -2*cos(2*pi*f0/fs); sig = filter([1 b1 1],1,sig); f0 = f0est(sig,fs,framesize,npartials,minlevel,debug) % Example output: % f0 = 439.99 % f0 = 437.50
Next Section:
A History of Spectral Audio Signal Processing
Previous Section:
Bilinear Frequency-Warping for Audio Spectrum Analysis over Bark and ERB Frequency Scales



















