Applications of the STFT
This chapter briefly tours selected applications involving spectral audio signal processing, with associated examples in matlab. Related historical background and techniques appear in Appendix G. Therefore, this chapter can focus more on practical methods known to the author regarding applications the Short-Time Fourier Transform (STFT) (defined and discussed in §7.1). The following applications are considered:
- fundamental frequency estimation from spectral peaks
- cross-synthesis
- spectral envelope extraction by cepstral smoothing
- spectral envelope extraction by linear prediction
- sinusoidal modeling of audio signals
- sines+noise modeling
- sines+noise+transients modeling
- chirplet modeling
- time-scale modification
- frequency scaling
- FFT filter banks
Fundamental Frequency Estimation from Spectral Peaks
Spectral peak measurement was discussed in Chapter 5.
Given a set of peak frequencies ![]() ,
,
![]() , it is usually
straightforward to form a fundamental frequency estimate
``
, it is usually
straightforward to form a fundamental frequency estimate
``![]() ''. This task is also called pitch detection, where the
perceived ``pitch'' of the audio signal is assumed to coincide well
enough with its fundamental frequency. We assume here that the signal
is periodic, so that all of its sinusoidal components are
harmonics of a fundamental component having frequency
''. This task is also called pitch detection, where the
perceived ``pitch'' of the audio signal is assumed to coincide well
enough with its fundamental frequency. We assume here that the signal
is periodic, so that all of its sinusoidal components are
harmonics of a fundamental component having frequency ![]() .
(For inharmonic sounds, the perceived pitch, if any, can be complex to
predict [54].)
.
(For inharmonic sounds, the perceived pitch, if any, can be complex to
predict [54].)
An approximate maximum-likelihood ![]() -detection
algorithm11.1 consists
of the following steps:
-detection
algorithm11.1 consists
of the following steps:
- Find the peak of the histogram of the
peak-frequency-differences in order to find the most common harmonic
spacing. This is the nominal
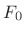 estimate. The matlab
hist function can be used to form a histogram from the
measured peak-spacings.
estimate. The matlab
hist function can be used to form a histogram from the
measured peak-spacings.
- Refine the nominal
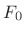 estimate using linear
regression. Linear regression simply fits a straight line through
the data to give a least-squares fit. In matlab, the function
polyfit(x,y,1) can be used, e.g., p =
polyfit([0,1],[1,1.5],1) returns p = [0.5,1], where
p(1) is the slope, and p(2) is the offset.
estimate using linear
regression. Linear regression simply fits a straight line through
the data to give a least-squares fit. In matlab, the function
polyfit(x,y,1) can be used, e.g., p =
polyfit([0,1],[1,1.5],1) returns p = [0.5,1], where
p(1) is the slope, and p(2) is the offset.
- The slope p(1) of the fitted line gives the
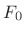 estimate.
estimate.
Useful Preprocessing
In many cases, results are improved through the use of preprocessing of the spectrum prior to peak finding. Examples include the following:
- Pre-emphasis: Equalize the spectrum so as to flatten it.
For example, low-order linear-prediction is often used for this purpose (the ``flattened''
spectrum is that of the prediction error). In voice coding, first-order linear
prediction is typically used [162].
- Masking: Small peaks close to much larger
peaks are often masked in the auditory system. Therefore, it
is good practice to reject all peaks below an inaudibility threshold
which is the maximum of the threshold of hearing (versus frequency)
and the masking pattern generated by the largest peaks
[16]. Since it is simple to extract peaks in
descending magnitude order, each removed peak can be replaced by its
masking pattern, which elevates the assumed inaudibility threshold.
Getting Closer to Maximum Likelihood
In applications for which the fundamental frequency ![]() must be
measured very accurately in a periodic signal, the estimate obtained
by the above algorithm can be refined using a gradient search
which matches a so-called harmonic comb to the magnitude
spectrum of an interpolated FFT
must be
measured very accurately in a periodic signal, the estimate obtained
by the above algorithm can be refined using a gradient search
which matches a so-called harmonic comb to the magnitude
spectrum of an interpolated FFT ![]() :
:
where
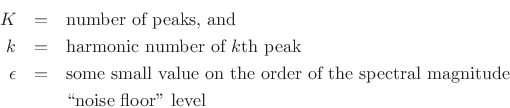
The purpose of
![]() is an insurance against multiplying the
whole expression by zero due to a missing partial (e.g., due to a
comb-filtering null). If
is an insurance against multiplying the
whole expression by zero due to a missing partial (e.g., due to a
comb-filtering null). If
![]() in (10.1), it is
advisable to omit indices
in (10.1), it is
advisable to omit indices ![]() for which
for which
![]() is too close to a
spectral null, since even one spectral null can push the product of
peak amplitudes to a very small value. At the same time, the product
should be penalized in some way to reflect the fact that it has fewer
terms (
is too close to a
spectral null, since even one spectral null can push the product of
peak amplitudes to a very small value. At the same time, the product
should be penalized in some way to reflect the fact that it has fewer
terms (
![]() is one way to accomplish this).
is one way to accomplish this).
As a practical matter, it is important to inspect the magnitude
spectra of the data frame manually to ensure that a robust row of
peaks is being matched by the harmonic comb. For example, it is
typical to look at a display of the frame magnitude spectrum overlaid
with vertical lines at the optimized harmonic-comb frequencies. This
provides an effective picture of the ![]() estimate in which typical
problems (such as octave errors) are readily seen.
estimate in which typical
problems (such as octave errors) are readily seen.
References on 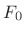 Estimation
Estimation
An often-cited book on classical methods for pitch detection,
particularly for voice, is that by Hess [106]. The
harmonic-comb method can be considered an approximate
maximum-likelihood estimator for fundamental frequency, and more
accurate maximum-likelihood methods have been worked out
[65,297,230,231].
Another highly regarded method for ![]() estimation is the YIN
algorithm [55]. For automatic transcription
of polyphonic music, Klapuri has developed methods for multiple
estimation is the YIN
algorithm [55]. For automatic transcription
of polyphonic music, Klapuri has developed methods for multiple ![]() estimation
[189,127,126,124].11.2Finally, a rich source of methods may be found in the conference
proceedings for the field of Music Information Retrieval
(MIR)11.3 Of course, don't
forget to try a Web search for ``F0 estimation'' and the like.
estimation
[189,127,126,124].11.2Finally, a rich source of methods may be found in the conference
proceedings for the field of Music Information Retrieval
(MIR)11.3 Of course, don't
forget to try a Web search for ``F0 estimation'' and the like.
Cross-Synthesis
Cross-synthesis is the technique of impressing the spectral envelope of one sound on the flattened spectrum of another. A typical example is to impress speech on various natural sounds, such as ``talking wind.'' Let's call the first signal the ``modulating'' signal, and the other the ``carrier'' signal. Then the modulator may be a voice, and the carrier may be any spectrally rich sound such as wind, rain, creaking noises, flute, or other musical instrument sound. Commercial ``vocoders'' (§G.10,§G.5) used as musical instruments consist of a keyboard synthesizer (for playing the carrier sounds) and a microphone for picking up the voice of the performer (to extract the modulation envelope).
Cross-synthesis may be summarized as consisting of the following steps:
- Perform a Short-Time Fourier Transform (STFT) of both the
modulator and carrier signals (§7.1).
- Compute the spectral envelope of each time-frame (as described
in the next section).
- Optionally divide the spectrum of each carrier frame by its own
spectral envelope, thereby flattening it.
- Multiply the flattened spectral frame by the envelope of the
corresponding modulator frame, thereby replacing the carrier's
envelope by the modulator's envelope.
http://ccrma.stanford.edu/~jos/SpecEnv/Application_Example_Cross_Synthesis.html
Spectral Envelope Extraction
There are many definitions of spectral envelope. Piecewise-linear (or polynomial spline) spectral envelopes (applied to the spectral magnitude of an STFT frame), have been used successfully in sines+noise modeling of audio signals (introduced in §10.4). Here we will consider spectral envelopes defined by the following two methods for computing them:
- cepstral windowing to lowpass-filter the log-magnitude
spectrum (a ``nonparametric method'')
- using linear prediction (a ``parametric method'') to capture spectral shape in the amplitude-response of an all-pole filter in a source-filter decomposition of the signal (where the source signal is defined to be spectrally flat)
In the following,
![]() denotes the
denotes the ![]() th spectral frame of
the STFT (§7.1), and
th spectral frame of
the STFT (§7.1), and
![]() denotes the spectral
envelope of
denotes the spectral
envelope of
![]() .
.
Cepstral Windowing
The spectral envelope obtained by cepstral windowing is defined as
![$\displaystyle Y_m \eqsp \hbox{\sc DFT}[w \cdot \underbrace{\hbox{\sc DFT}^{-1}\log(\vert X_m\vert)}_{\hbox{real cepstrum}}]$](http://www.dsprelated.com/josimages_new/sasp2/img1728.png) |
(11.2) |
where
![$\displaystyle w(n) \eqsp \left\{\begin{array}{ll} 1, & \vert n\vert< n_c \\ [5pt] 0.5, & \vert n\vert=n_c \\ [5pt] 0, & \vert n\vert>n_c, \\ \end{array} \right.$](http://www.dsprelated.com/josimages_new/sasp2/img1729.png) |
(11.3) |
where
The log-magnitude spectrum of ![]() is thus lowpass filtered
(the real cepstrum of
is thus lowpass filtered
(the real cepstrum of ![]() is ``liftered'') to obtain a smooth spectral
envelope. For periodic signals,
is ``liftered'') to obtain a smooth spectral
envelope. For periodic signals, ![]() should be set below the period
in samples.
should be set below the period
in samples.
Cepstral coefficients are typically used in speech recognition to characterize spectral envelopes, capturing primarily the formants (spectral resonances) of speech [227]. In audio applications, a warped frequency axis, such as the ERB scale (Appendix E), Bark scale, or Mel frequency scale is typically preferred. Mel Frequency Cepstral Coefficients (MFCC) appear to remain quite standard in speech-recognition front ends, and they are often used to characterize steady-state spectral timbre in Music Information Retrieval (MIR) applications.
Linear Prediction Spectral Envelope
Linear Prediction (LP) implicitly computes a spectral envelope that is well adapted for audio work, provided the order of the predictor is appropriately chosen. Due to the error minimized by LP, spectral peaks are emphasized in the envelope, as they are in the auditory system. (The peak-emphasis of LP is quantified in (10.10) below.)
The term ``linear prediction'' refers to the process of predicting a
signal sample ![]() based on
based on ![]() past samples:
past samples:
We call
Taking the z transform of (10.4) yields
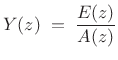 |
(11.5) |
where
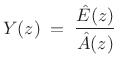 |
(11.6) |
where
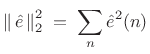 |
(11.7) |
over some range of
If the prediction-error is successfully whitened, then the signal model can be expressed in the frequency domain as
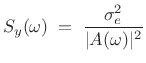 |
(11.8) |
where
| EnvelopeLPC |
(11.9) |
Linear Prediction is Peak Sensitive
By Rayleigh's energy theorem,
![]() (as
shown in §2.3.8). Therefore,
(as
shown in §2.3.8). Therefore,
From this ``ratio error'' expression in the frequency domain, we can see that contributions to the error are smallest when
Linear Prediction Methods
The two classic methods for linear prediction are called the autocorrelation method and the covariance method [162,157]. Both methods solve the linear normal equations (defined below) using different autocorrelation estimates.
In the autocorrelation method of linear prediction, the covariance
matrix is constructed from the usual Bartlett-window-biased sample
autocorrelation function (see Chapter 6), and it has the
desirable property that
![]() is always minimum phase (i.e.,
is always minimum phase (i.e.,
![]() is guaranteed to be stable). However, the autocorrelation
method tends to overestimate formant bandwidths; in other words, the
filter model is typically overdamped. This can be attributed to
implicitly ``predicting zero'' outside of the signal frame, resulting
in the Bartlett-window bias in the sample autocorrelation.
is guaranteed to be stable). However, the autocorrelation
method tends to overestimate formant bandwidths; in other words, the
filter model is typically overdamped. This can be attributed to
implicitly ``predicting zero'' outside of the signal frame, resulting
in the Bartlett-window bias in the sample autocorrelation.
The covariance method of LP is based on an unbiased
autocorrelation estimate (see Eq.![]() (6.4)). As a result, it
gives more accurate bandwidths, but it does not guarantee stability.
(6.4)). As a result, it
gives more accurate bandwidths, but it does not guarantee stability.
So-called covariance lattice methods and Burg's method were developed to maintain guaranteed stability while giving accuracy comparable to the covariance method of LP [157].
Computation of Linear Prediction Coefficients
In the autocorrelation method of linear prediction, the linear
prediction coefficients
![]() are computed from the
Bartlett-window-biased autocorrelation function
(Chapter 6):
are computed from the
Bartlett-window-biased autocorrelation function
(Chapter 6):
where
In matlab syntax, the solution is given by ``
If the rank of the ![]() autocorrelation matrix
autocorrelation matrix
![]() is
is ![]() , then the solution to (10.12)
is unique, and
this solution is always minimum phase [162] (i.e., all roots of
, then the solution to (10.12)
is unique, and
this solution is always minimum phase [162] (i.e., all roots of
![]() are inside the unit circle in the
are inside the unit circle in the ![]() plane [263], so
that
plane [263], so
that ![]() is always a stable all-pole filter). In
practice, the rank of
is always a stable all-pole filter). In
practice, the rank of ![]() is
is ![]() (with probability 1) whenever
(with probability 1) whenever ![]() includes a noise component. In the noiseless case, if
includes a noise component. In the noiseless case, if ![]() is a sum
of sinusoids, each (real) sinusoid at distinct frequency
is a sum
of sinusoids, each (real) sinusoid at distinct frequency
![]() adds 2 to the rank. A dc component, or a component at half the
sampling rate, adds 1 to the rank of
adds 2 to the rank. A dc component, or a component at half the
sampling rate, adds 1 to the rank of ![]() .
.
The choice of time window for forming a short-time sample
autocorrelation and its weighting also affect the rank of
![]() . Equation (10.11) applied to a finite-duration frame yields what is
called the autocorrelation method of linear
prediction [162]. Dividing out the Bartlett-window bias in such a
sample autocorrelation yields a result closer to the covariance method
of LP. A matlab example is given in §10.3.3 below.
. Equation (10.11) applied to a finite-duration frame yields what is
called the autocorrelation method of linear
prediction [162]. Dividing out the Bartlett-window bias in such a
sample autocorrelation yields a result closer to the covariance method
of LP. A matlab example is given in §10.3.3 below.
The classic covariance method computes an unbiased sample covariance
matrix by limiting the summation in (10.11) to a range over which
![]() stays within the frame--a so-called ``unwindowed'' method.
The autocorrelation method sums over the whole frame and replaces
stays within the frame--a so-called ``unwindowed'' method.
The autocorrelation method sums over the whole frame and replaces
![]() by zero when
by zero when ![]() points outside the frame--a so-called
``windowed'' method (windowed by the rectangular window).
points outside the frame--a so-called
``windowed'' method (windowed by the rectangular window).
Linear Prediction Order Selection
For computing spectral envelopes via linear prediction, the order ![]() of the predictor should be chosen large enough that the envelope can
follow the contour of the spectrum, but not so large that it follows
the spectral ``fine structure'' on a scale not considered to belong in
the envelope. In particular, for voice,
of the predictor should be chosen large enough that the envelope can
follow the contour of the spectrum, but not so large that it follows
the spectral ``fine structure'' on a scale not considered to belong in
the envelope. In particular, for voice, ![]() should be twice the
number of spectral formants, and perhaps a little larger to
allow more detailed modeling of spectral shape away from the formants.
For a sum of quasi sinusoids, the order
should be twice the
number of spectral formants, and perhaps a little larger to
allow more detailed modeling of spectral shape away from the formants.
For a sum of quasi sinusoids, the order ![]() should be significantly
less than twice the number of sinusoids to inhibit modeling the
sinusoids as spectral-envelope peaks. For filtered-white-noise,
should be significantly
less than twice the number of sinusoids to inhibit modeling the
sinusoids as spectral-envelope peaks. For filtered-white-noise, ![]() should be close to the order of the filter applied to the white noise,
and so on.
should be close to the order of the filter applied to the white noise,
and so on.
Summary of LP Spectral Envelopes
In summary, the spectral envelope of the ![]() th spectral frame,
computed by linear prediction, is given by
th spectral frame,
computed by linear prediction, is given by
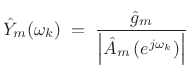 |
(11.13) |
where
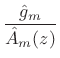 |
(11.14) |
can be driven by unit-variance white noise to produce a filtered-white-noise signal having spectral envelope
It bears repeating that
![]() is zero mean when
is zero mean when
![]() is monic and minimum phase (all zeros inside the unit circle).
This means, for example, that
is monic and minimum phase (all zeros inside the unit circle).
This means, for example, that
![]() can be simply estimated as
the mean of the log spectral magnitude
can be simply estimated as
the mean of the log spectral magnitude
![]() .
.
For best results, the frequency axis ``seen'' by linear prediction should be warped to an auditory frequency scale, as discussed in Appendix E [123]. This has the effect of increasing the accuracy of low-frequency peaks in the extracted spectral envelope, in accordance with the nonuniform frequency resolution of the inner ear.
Spectral Envelope Examples
This section presents matlab code for computing spectral envelopes by the cepstral and linear prediction methods discussed above. The signal to be modeled is a synthetic ``ah'' vowel (as in ``father'') synthesized using three formants driven by a bandlimited impulse train [128].
Signal Synthesis
% Specify formant resonances for an "ah" [a] vowel: F = [700, 1220, 2600]; % Formant frequencies in Hz B = [130, 70, 160]; % Formant bandwidths in Hz fs = 8192; % Sampling rate in Hz % ("telephone quality" for speed) R = exp(-pi*B/fs); % Pole radii theta = 2*pi*F/fs; % Pole angles poles = R .* exp(j*theta); [B,A] = zp2tf(0,[poles,conj(poles)],1); f0 = 200; % Fundamental frequency in Hz w0T = 2*pi*f0/fs; nharm = floor((fs/2)/f0); % number of harmonics nsamps = fs; % make a second's worth sig = zeros(1,nsamps); n = 0:(nsamps-1); % Synthesize bandlimited impulse train: for i=1:nharm, sig = sig + cos(i*w0T*n); end; sig = sig/max(sig); soundsc(sig,fs); % Let's hear it % Now compute the speech vowel: speech = filter(1,A,sig); soundsc([sig,speech],fs); % "buzz", "ahh" % (it would sound much better with a little vibrato)
The Hamming-windowed bandlimited impulse train sig and its spectrum are plotted in Fig.10.1.
Figure 10.2 shows the Hamming-windowed synthesized vowel speech, and its spectrum overlaid with the true formant envelope.
Spectral Envelope by the Cepstral Windowing Method
We now compute the log-magnitude spectrum, perform an inverse FFT to obtain the real cepstrum, lowpass-window the cepstrum, and perform the FFT to obtain the smoothed log-magnitude spectrum:
Nframe = 2^nextpow2(fs/25); % frame size = 40 ms w = hamming(Nframe)'; winspeech = w .* speech(1:Nframe); Nfft = 4*Nframe; % factor of 4 zero-padding sspec = fft(winspeech,Nfft); dbsspecfull = 20*log(abs(sspec)); rcep = ifft(dbsspecfull); % real cepstrum rcep = real(rcep); % eliminate round-off noise in imag part period = round(fs/f0) % 41 nspec = Nfft/2+1; aliasing = norm(rcep(nspec-10:nspec+10))/norm(rcep) % 0.02 nw = 2*period-4; % almost 1 period left and right if floor(nw/2) == nw/2, nw=nw-1; end; % make it odd w = boxcar(nw)'; % rectangular window wzp = [w(((nw+1)/2):nw),zeros(1,Nfft-nw), ... w(1:(nw-1)/2)]; % zero-phase version wrcep = wzp .* rcep; % window the cepstrum ("lifter") rcepenv = fft(wrcep); % spectral envelope rcepenvp = real(rcepenv(1:nspec)); % should be real rcepenvp = rcepenvp - mean(rcepenvp); % normalize to zero mean
Figure 10.3 shows the real cepstrum of the synthetic ``ah'' vowel (top) and the same cepstrum truncated to just under a period in length. In theory, this leaves only formant envelope information in the cepstrum. Figure 10.4 shows an overlay of the spectrum, true envelope, and cepstral envelope.
Instead of simply truncating the cepstrum (a rectangular windowing operation), we can window it more gracefully. Figure 10.5 shows the result of using a Hann window of the same length. The spectral envelope is smoother as a result.
Spectral Envelope by Linear Prediction
Finally, let's do an LPC window. It had better be good because the LPC model is exact for this example.
M = 6; % Assume three formants and no noise % compute Mth-order autocorrelation function: rx = zeros(1,M+1)'; for i=1:M+1, rx(i) = rx(i) + speech(1:nsamps-i+1) ... * speech(1+i-1:nsamps)'; end % prepare the M by M Toeplitz covariance matrix: covmatrix = zeros(M,M); for i=1:M, covmatrix(i,i:M) = rx(1:M-i+1)'; covmatrix(i:M,i) = rx(1:M-i+1); end % solve "normal equations" for prediction coeffs: Acoeffs = - covmatrix \ rx(2:M+1) Alp = [1,Acoeffs']; % LP polynomial A(z) dbenvlp = 20*log10(abs(freqz(1,Alp,nspec)')); dbsspecn = dbsspec + ones(1,nspec)*(max(dbenvlp) ... - max(dbsspec)); % normalize plot(f,[max(dbsspecn,-100);dbenv;dbenvlp]); grid;
Linear Prediction in Matlab and Octave
In the above example, we implemented essentially the covariance method of LP directly (the autocorrelation estimate was unbiased). The code should run in either Octave or Matlab with the Signal Processing Toolbox.
The Matlab Signal Processing Toolbox has the function lpc available. (LPC stands for ``Linear Predictive Coding.'')
The Octave-Forge lpc function (version 20071212) is a wrapper
for the lattice function which implements Burg's method by
default. Burg's method has the advantage of guaranteeing stability
(![]() is minimum phase) while yielding accuracy comparable to the
covariance method. By uncommenting lines in lpc.m, one can
instead use the ``geometric lattice'' or classic autocorrelation
method (called ``Yule-Walker'' in lpc.m). For details,
``type lpc''.
is minimum phase) while yielding accuracy comparable to the
covariance method. By uncommenting lines in lpc.m, one can
instead use the ``geometric lattice'' or classic autocorrelation
method (called ``Yule-Walker'' in lpc.m). For details,
``type lpc''.
Spectral Modeling Synthesis
This section reviews elementary spectral models for sound synthesis. Spectral models are well matched to audio perception because the ear is a kind of spectrum analyzer [293].
For periodic sounds, the component sinusoids are all
harmonics of a fundamental at frequency ![]() :
:
where
Aperiodic sounds can similarly be expressed as a continuous sum of sinusoids at potentially all frequencies in the range of human hearing:11.6
where
Sinusoidal models are most appropriate for ``tonal'' sounds such as
spoken or sung vowels, or the sounds of musical instruments in the
string, wind, brass, and ``tonal percussion'' families. Ideally, one
sinusoid suffices to represent each harmonic or overtone.11.7 To represent the ``attack'' and ``decay''
of natural tones, sinusoidal components are multiplied by an
amplitude envelope that varies over time. That is, the
amplitude ![]() in (10.15) is a slowly varying function of time;
similarly, to allow pitch variations such as vibrato, the phase
in (10.15) is a slowly varying function of time;
similarly, to allow pitch variations such as vibrato, the phase
![]() may be modulated in various ways.11.8 Sums of
amplitude- and/or frequency-enveloped sinusoids are generally called
additive synthesis (discussed further in §10.4.1
below).
may be modulated in various ways.11.8 Sums of
amplitude- and/or frequency-enveloped sinusoids are generally called
additive synthesis (discussed further in §10.4.1
below).
Sinusoidal models are ``unreasonably effective'' for tonal audio. Perhaps the main reason is that the ear focuses most acutely on peaks in the spectrum of a sound [179,305]. For example, when there is a strong spectral peak at a particular frequency, it tends to mask lower level sound energy at nearby frequencies. As a result, the ear-brain system is, to a first approximation, a ``spectral peak analyzer''. In modern audio coders [16,200] exploiting masking results in an order-of-magnitude data compression, on average, with no loss of quality, according to listening tests [25]. Thus, we may say more specifically that, to first order, the ear-brain system acts like a ``top ten percent spectral peak analyzer''.
For noise-like sounds, such as wind, scraping sounds, unvoiced speech, or breath-noise in a flute, sinusoidal models are relatively expensive, requiring many sinusoids across the audio band to model noise. It is therefore helpful to combine a sinusoidal model with some kind of noise model, such as pseudo-random numbers passed through a filter [249]. The ``Sines + Noise'' (S+N) model was developed to use filtered noise as a replacement for many sinusoids when modeling noise (to be discussed in §10.4.3 below).
Another situation in which sinusoidal models are inefficient is at sudden time-domain transients in a sound, such as percussive note onsets, ``glitchy'' sounds, or ``attacks'' of instrument tones more generally. From Fourier theory, we know that transients, too, can be modeled exactly, but only with large numbers of sinusoids at exactly the right phases and amplitudes. To obtain a more compact signal model, it is better to introduce an explicit transient model which works together with sinusoids and filtered noise to represent the sound more parsimoniously. Sines + Noise + Transients (S+N+T) models were developed to separately handle transients (§10.4.4).
A advantage of the explicit transient model in S+N+T models is that transients can be preserved during time-compression or expansion. That is, when a sound is stretched (without altering its pitch), it is usually desirable to preserve the transients (i.e., to keep their local time scales unchanged) and simply translate them to new times. This topic, known as Time-Scale Modification (TSM) will be considered further in §10.5 below.
In addition to S+N+T components, it is useful to superimpose spectral weightings to implement linear filtering directly in the frequency domain; for example, the formants of the human voice are conveniently impressed on the spectrum in this way (as illustrated §10.3 above) [174].11.9 We refer to the general class of such frequency-domain signal models as spectral models, and sound synthesis in terms of spectral models is often called spectral modeling synthesis (SMS).
The subsections below provide a summary review of selected aspects of spectral modeling, with emphasis on applications in musical sound synthesis and effects.
Additive Synthesis (Early Sinusoidal Modeling)
Additive synthesis is evidently the first technique widely used for
analysis and synthesis of audio in computer music
[232,233,184,186,187].
It was inspired directly by Fourier theory
[264,23,36,150] (which followed Daniel
Bernoulli's insights (§G.1)) which states that any sound
![]() can be expressed mathematically as a sum of sinusoids. The
`term ``additive synthesis'' refers to sound being formed by adding
together many sinusoidal components modulated by relatively
slowly varying amplitude and frequency envelopes:
can be expressed mathematically as a sum of sinusoids. The
`term ``additive synthesis'' refers to sound being formed by adding
together many sinusoidal components modulated by relatively
slowly varying amplitude and frequency envelopes:
![$\displaystyle y(t)= \sum\limits_{i=1}^{N} A_i(t)\sin[\theta_i(t)]$](http://www.dsprelated.com/josimages_new/sasp2/img1799.png) |
(11.17) |
where
and all quantities are real. Thus, each sinusoid may have an independently time-varying amplitude and/or phase, in general. The amplitude and frequency envelopes are determined from some kind of short-time Fourier analysis as discussed in Chapters 8 and 9) [62,187,184,186].
An additive-synthesis oscillator-bank is shown in Fig.10.7, as
it is often drawn in computer music [235,234]. Each
sinusoidal oscillator [166]
accepts an amplitude envelope ![]() (e.g., piecewise linear,
or piecewise exponential) and a frequency envelope
(e.g., piecewise linear,
or piecewise exponential) and a frequency envelope ![]() ,
also typically piecewise linear or exponential. Also shown in
Fig.10.7 is a filtered noise input, as used in S+N
modeling (§10.4.3).
,
also typically piecewise linear or exponential. Also shown in
Fig.10.7 is a filtered noise input, as used in S+N
modeling (§10.4.3).
Additive Synthesis Analysis
In order to reproduce a given signal, we must first analyze it
to determine the amplitude and frequency trajectories for each
sinusoidal component. We do not need phase information (![]() in (10.18)) during steady-state segments, since phase is normally
not perceived in steady state tones [293,211].
However, we do need phase information for analysis frames containing an
attack transient, or any other abrupt change in the signal.
The phase of the sinusoidal peaks controls the position of time-domain
features of the waveform within the analysis frame.
in (10.18)) during steady-state segments, since phase is normally
not perceived in steady state tones [293,211].
However, we do need phase information for analysis frames containing an
attack transient, or any other abrupt change in the signal.
The phase of the sinusoidal peaks controls the position of time-domain
features of the waveform within the analysis frame.
Following Spectral Peaks
In the analysis phase, sinusoidal peaks are measured over time in a sequence of FFTs, and these peaks are grouped into ``tracks'' across time. A detailed discussion of various options for this can be found in [246,174,271,84,248,223,10,146], and a particular case is detailed in Appendix H.
The end result of the analysis pass is a collection of amplitude and
frequency envelopes for each spectral peak versus time. If the time
advance from one FFT to the next is fixed (5ms is a typical choice for
speech analysis), then we obtain uniformly sampled amplitude and
frequency trajectories as the result of the analysis. The sampling
rate of these amplitude and frequency envelopes is equal to
the frame rate of the analysis. (If the time advance between
FFTs is
![]() ms, then the frame rate is defined as
ms, then the frame rate is defined as
![]() Hz.) For resynthesis using inverse FFTs, these data may be
used unmodified. For resynthesis using a bank of sinusoidal
oscillators, on the other hand, we must somehow
interpolate the envelopes to create envelopes at the signal
sampling rate (typically
Hz.) For resynthesis using inverse FFTs, these data may be
used unmodified. For resynthesis using a bank of sinusoidal
oscillators, on the other hand, we must somehow
interpolate the envelopes to create envelopes at the signal
sampling rate (typically ![]() kHz or higher).
kHz or higher).
It is typical in computer music to linearly interpolate the
amplitude and frequency trajectories from one frame to the next
[271].11.10 Let's call the piecewise-linear upsampled envelopes
![]() and
and
![]() , defined now for all
, defined now for all ![]() at the normal signal
sampling rate. For steady-state tonal sounds, the phase may be
discarded at this stage and redefined as the integral of the
instantaneous frequency when needed:
at the normal signal
sampling rate. For steady-state tonal sounds, the phase may be
discarded at this stage and redefined as the integral of the
instantaneous frequency when needed:
When phase must be matched in a given frame, such as when it is known to contain a transient event, the frequency can instead move quadratically across the frame to provide cubic phase interpolation [174], or a second linear breakpoint can be introduced somewhere in the frame for the frequency trajectory (in which case the area under the triangle formed by the second breakpoint equals the added phase at the end of the segment).
Sinusoidal Peak Finding
For each sinusoidal component of a signal, we need to determine its
frequency, amplitude, and phase (when needed). As a starting point,
consider the windowed complex sinusoid with complex amplitude
![]() and frequency
and frequency ![]() :
:
| (11.20) |
As discussed in Chapter 5, the transform (DTFT) of this windowed signal is the convolution of a frequency domain delta function at
![\begin{eqnarray*}
X_w(\omega) &=& \sum_{n=-\infty}^{\infty}[w(n)x(n)]e^{ -j\omega nT}
\qquad\hbox{(DTFT($x_w$))} \\
&=& \sum_{n=-(M-1)/2}^{(M-1)/2} \left[w(n){\cal A}_xe^{j\omega_xnT}\right]e^{ -j\omega nT}\\
&=& {\cal A}_x\sum_n w(n) e^{-j(\omega-\omega_x)nT} \\
&=& \zbox {{\cal A}_xW(\omega-\omega_x)}
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img1822.png)
Hence,
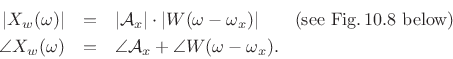
At ![]() , we have
, we have
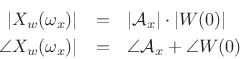
If we scale the window to have a dc gain of 1, then the peak magnitude
equals the amplitude of the sinusoid, i.e.,
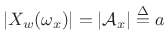 , as shown in Fig.10.8.
, as shown in Fig.10.8.
If we use a zero-phase (even) window, the phase at the peak equals the
phase of the sinusoid, i.e.,
![]() .
.
Tracking Sinusoidal Peaks in a Sequence of FFTs
The preceding discussion focused on estimating sinusoidal peaks in a single frame of data. For estimating sinusoidal parameter trajectories through time, it is necessary to associate peaks from one frame to the next. For example, Fig.10.9 illustrates a set of frequency trajectories, including one with a missing segment due to its peak not being detected in the third frame.
Figure 10.10 depicts a basic analysis system for tracking spectral peaks in the STFT [271]. The system tracks peak amplitude, center-frequency, and sometimes phase. Quadratic interpolation is used to accurately find spectral magnitude peaks (§5.7). For further analysis details, see Appendix H. Synthesis is performed using a bank of amplitude- and phase-modulated oscillators, as shown in Fig.10.7. Alternatively, the sinusoids are synthesized using an inverse FFT [239,94,139].
Sines + Noise Modeling
As mentioned in the introduction to this chapter, it takes many sinusoidal components to synthesize noise well (as many as 25 per critical band of hearing under certain conditions [85]). When spectral peaks are that dense, they are no longer perceived individually, and it suffices to match only their statistics to a perceptually equivalent degree.
Sines+Noise (S+N) synthesis [249] generalizes the
sinusoidal signal models to include a filtered noise component,
as depicted in Fig.10.7. In that figure, white noise is
denoted by ![]() , and the slowly changing linear filter applied to
the noise at time
, and the slowly changing linear filter applied to
the noise at time ![]() is denoted
is denoted
![]() .
.
The time-varying spectrum of the signal is said to be made up of a deterministic component (the sinusoids) and a stochastic component (time-varying filtered noise) [246,249]:
![$\displaystyle s(t) \eqsp \sum_{i=1}^{N} A_i(t) \cos[ \theta_i(t)] + e(t),$](http://www.dsprelated.com/josimages_new/sasp2/img1832.png) |
(11.21) |
where
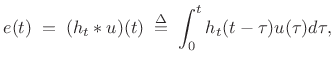 |
(11.22) |
where
Filtering white-noise to produce a desired timbre is an example of subtractive synthesis [186]. Thus, additive synthesis is nicely supplemented by subtractive synthesis as well.
Sines+Noise Analysis
The original sines+noise analysis method is shown in Fig.10.11 [246,249]. The processing path along the top from left to right measures the amplitude and frequency trajectories from magnitude peaks in the STFT, as in Fig.10.10. The peak amplitude and frequency trajectories are converted back to the time domain by additive-synthesis (an oscillator bank or inverse FFT), and this signal is windowed by the same analysis window and forward-transformed back into the frequency domain. The magnitude-spectrum of this sines-only data is then subtracted from the originally computed magnitude-spectrum containing both peaks and ``noise''. The result of this subtraction is termed the residual signal. The upper spectral envelope of the residual magnitude spectrum is measured using, e.g., linear prediction, cepstral smoothing, as discussed in §10.3 above, or by simply connecting peaks of the residual spectrum with linear segments to form a more traditional (in computer music) piecewise linear spectral envelope.
S+N Synthesis
A sines+noise synthesis diagram is shown in Fig.10.12. The spectral-peak amplitude and frequency trajectories are possibly modified (time-scaling, frequency scaling, virtual formants, etc.) and then rendered into the time domain by additive synthesis. This is termed the deterministic part of the synthesized signal.
The stochastic part is synthesized by applying the residual-spectrum-envelope (a time-varying FIR filter) to white noise, again after possible modifications to the envelope.
To synthesize a frame of filtered white noise, one can simply impart a
random phase to the spectral envelope, i.e., multiply it by
![]() , where
, where
![]() is random and
uniformly distributed between
is random and
uniformly distributed between ![]() and
and ![]() . In the time domain,
the synthesized white noise will be approximately Gaussian due
to the central limit theorem (§D.9.1). Because the
filter (spectral envelope) is changing from frame to frame through
time, it is important to use at least 50% overlap and non-rectangular
windowing in the time domain. The window can be implemented directly
in the frequency domain by convolving its transform with the complex
white-noise spectrum (§3.3.5), leaving only overlap-add to be
carried out in the time domain. If the window side-lobes can be fully
neglected, it suffices to use only main lobe in such a convolution
[239].
. In the time domain,
the synthesized white noise will be approximately Gaussian due
to the central limit theorem (§D.9.1). Because the
filter (spectral envelope) is changing from frame to frame through
time, it is important to use at least 50% overlap and non-rectangular
windowing in the time domain. The window can be implemented directly
in the frequency domain by convolving its transform with the complex
white-noise spectrum (§3.3.5), leaving only overlap-add to be
carried out in the time domain. If the window side-lobes can be fully
neglected, it suffices to use only main lobe in such a convolution
[239].
In Fig.10.12, the deterministic and stochastic components are summed after transforming to the time domain, and this is the typical choice when an explicit oscillator bank is used for the additive synthesis. When the IFFT method is used for sinusoid synthesis [239,94,139], the sum can occur in the frequency domain, so that only one inverse FFT is required.
Sines+Noise Summary
To summarize, sines+noise modeling is carried out by a procedure such as the following:
- Compute a sinusoidal model by tracking peaks across STFT
frames, producing a set of amplitude envelopes
 and
frequency envelopes
and
frequency envelopes 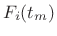 , where
, where  is the frame number and
is the frame number and
 is the spectral-peak number.
is the spectral-peak number.
- Also record phase
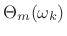 for frames
containing a transient.
for frames
containing a transient.
- Subtract modeled peaks from each STFT spectrum to form a
residual spectrum.
- Fit a smooth spectral envelope
 to each
residual spectrum.
to each
residual spectrum.
- Convert envelopes to reduced form, e.g., piecewise linear
segments with nonuniformly distributed breakpoints (optimized to be
maximally sparse without introducing audible distortion).
- Resynthesize audio (along with any desired transformations) from
the amplitude, frequency, and noise-floor-filter envelopes.
- Alter frequency trajectories slightly to hit the desired phase
for transient frames (as described below equation
Eq.
 (10.19)).
(10.19)).
Because the signal model consists entirely of envelopes (neglecting the phase data for transient frames), the signal model is easily time scaled, as discussed further in §10.5 below.
For more information on sines+noise signal modeling, see, e.g., [146,10,223,248,246,149,271,248,271]. A discussion from an historical perspective appears in §G.11.4.
Sines + Noise + Transients Models
As we have seen, sinusoids efficiently model spectral peaks over time, and filtered noise efficiently models the spectral residual left over after pulling out everything we want to call a ``tonal component'' characterized by a spectral peak the evolves over time. However, neither is good for abrupt transients in a waveform. At transients, one may retain the original waveform or some compressed version of it (e.g., MPEG-2 AAC with short window [149]). Alternatively, one may switch to a transient model during transients. Transient models have included wavelet expansion [6] and frequency-domain LPC (time-domain amplitude envelope) [290].
In either case, a reliable transient detector is needed. This
can raise deep questions regarding what a transient really is; for
example, not everyone will notice every transient as a transient, and
so perceptual modeling gets involved. Missing a transient, e.g., in a
ride-cymbal analysis, can create highly audible artifacts when
processing heavily based on transient decisions. For greater
robustness, hybrid schemes can be devised in which a continuous
measure of ``transientness'' ![]() can be defined between 0 and 1,
say.
can be defined between 0 and 1,
say.
Also in either case, the sinusoidal model needs phase matching when switching to or from a transient frame over time (or cross-fading can be used, or both). Given sufficiently many sinusoids, phase-matching at the switching time should be sufficient without cross-fading.
Sines+Noise+Transients Time-Frequency Maps
Figure 10.13 shows the multiresolution time-frequency map used in the original S+N+T system [149]. (Recall the fixed-resolution STFT time-frequency map in Fig.7.1.) Vertical line spacing in the time-frequency map indicates the time resolution of the underlying multiresolution STFT,11.11 and the horizontal line spacing indicates its frequency resolution. The time waveform appears below the time-frequency map. For transients, an interval of data including the transient is simply encoded using MPEG-2 AAC. The transient-time in Fig.10.13 extends from approximately 47 to 115 ms. (This interval can be tighter, as discussed further below.) Between transients, the signal model consists of sines+noise below 5 kHz and amplitude-modulated noise above. The spectrum from 0 to 5 kHz is divided into three octaves (``multiresolution sinusoidal modeling''). The time step-size varies from 25 ms in the low-frequency band (where the frequency resolution is highest), down to 6 ms in the third octave (where frequency resolution is four times lower). In the 0-5 kHz band, sines+noise modeling is carried out. Above 5 kHz, noise substitution is performed, as discussed further below.
Figure 10.14 shows a similar map in which the transient interval depends on frequency. This enables a tighter interval enclosing the transient, and follows audio perception more closely (see Appendix E).
Sines+Noise+Transients Noise Model
Figure 10.15 illustrates the nature of the noise modeling used in [149]. The energy in each Bark band11.12 is summed, and this is used as the gain for the noise in that band at that frame time.
Figure 10.16 shows the frame gain versus time for a particular Bark band (top) and the piecewise linear envelope made from it (bottom). As illustrated in Figures 10.13 and 10.14, the step size for all of the Bark bands above 5 kHz is approximately 3 ms.
S+N+T Sound Examples
A collection of sound examples illustrating sines+noise+transients
modeling (and various subsets thereof) as well as some audio effects
made possible by such representations, can be found online at
http://ccrma.stanford.edu/~jos/pdf/SMS.pdf.
Discussion regarding S+N+T models in historical context is given in §G.11.5.
Time Scale Modification
Time Scale Modification (TSM) means speeding up or slowing down a sound without affecting the frequency content, such as the perceived pitch of any tonal components. For example, TSM of speech should sound like the speaker is talking at a slower or faster pace, without distortion of the spoken vowels. Similarly, TSM of music should change timing but not tuning.
When a recorded speech signal is simply played faster, such as by lowering its sampling-rate and playing it at the original sampling-rate, the pace of the speech increases as desired, but so does the fundamental frequency (pitch contour). Moreover, the apparent ``head size'' of the speaker shrinks (the so-called ``munchkinization'' effect). This happens because, as illustrated in §10.3, speech spectra have formants (resonant peaks) which should not be moved when the speech rate is varied. The average formant spacing in frequency is a measure of the length of the vocal tract; hence, when speech is simply played faster, the average formant spacing decreases, corresponding to a smaller head size. This illusion of size modulation can be a useful effect in itself, such as for scaling the apparent size of virtual musical instruments using commuted synthesis [47,266]. However, we also need to be able to adjust time scales without this overall scaling effect.
The Fourier dual of time-scale modification is frequency scaling. In this case, we wish to scale the spectral content of a signal up or down without altering the timing of sonic events in the time domain. This effect is used, for example, to retune ``bad notes'' in a recording studio. Frequency scaling can be implemented as TSM preceded or followed by sampling-rate conversion, or it can be implemented directly in a sequence of STFT frames like TSM.
TSM and S+N+T
Time Scale Modification (TSM), and/or frequency scaling, are
relatively easy to implement in a sines+noise+transient (S+N+T) model
(§10.4.4). Figure 10.17 illustrates schematically
how it works. For TSM, the envelopes of the sinusoidal and noise
models are simply stretched or squeezed versus time as desired, while
the time-intervals containing transients are only translated
forward or backward in time--not time-scaled. As a result,
transients are not ``smeared out'' when time-expanding, or otherwise
distorted by TSM. If a ``transientness'' measure ![]() is defined,
it can be used to control how ``rubbery'' a given time-segment is;
that is, for
is defined,
it can be used to control how ``rubbery'' a given time-segment is;
that is, for
![]() , the interval is rigid and can only translate
in time, while for
, the interval is rigid and can only translate
in time, while for
![]() it is allowed stretch and squeeze along
with the adjacent S+N model. In between 0 and 1, the time-interval
scales less than the S+N model. See [149] for more details
regarding TSM in an S+N+T framework.
it is allowed stretch and squeeze along
with the adjacent S+N model. In between 0 and 1, the time-interval
scales less than the S+N model. See [149] for more details
regarding TSM in an S+N+T framework.
TSM by Resampling STFTs Across Time
In view of Chapter 8, a natural implementation of TSM based on the STFT is as follows:
- Perform a short-time Fourier transform (STFT) using hop size
 . Denote the STFT at frame
. Denote the STFT at frame  and bin
and bin  by
by
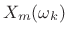 , and
denote the result of TSM processing by
, and
denote the result of TSM processing by
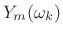 .
.
- To perform TSM by the factor
 , advance the ``frame
pointer''
, advance the ``frame
pointer''  by
by 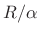 during resynthesis instead of the usual
during resynthesis instead of the usual
 samples.
samples.
For example, if ![]() (
(![]() slow-down), the first STFT frame
slow-down), the first STFT frame
![]() is processed normally, so that
is processed normally, so that ![]() . However, the
second output frame
. However, the
second output frame ![]() corresponds to a time
corresponds to a time ![]() , half way
between the first two frames. This output frame may be created by
interpolating (across time) the STFT magnitude magnitude
spectra of the first. For example, using simple linear interpolation
gives
, half way
between the first two frames. This output frame may be created by
interpolating (across time) the STFT magnitude magnitude
spectra of the first. For example, using simple linear interpolation
gives
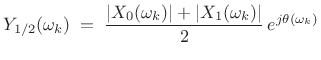 |
(11.23) |
where the phase
| (11.24) |
where
In general, TSM methods based on STFT modification are classified as ``vocoder'' type methods (§G.5). Thus, the TSM implementation outlined above may be termed a weighted overlap-add (WOLA) phase-vocoder method.
Phase Continuation
When interpolating the STFT across time for TSM, it is straightforward to interpolate spectral magnitude, as we saw above. Interpolating spectral phase, on the other hand, is tricky, because there's no exact way to do it [220]. There are two conflicting desiderata when deciding how to continue phase from one frame to the next:
- (1)
- Sinusoids should ``pick up where they left off'' in the previous frame.
- (2)
- The relative phase from bin to bin should be preserved in each FFT.
When condition (2) is violated, the signal frame suffers dispersion in the time domain. For steady-state signals (filtered noise and/or steady tones), temporal dispersion should not be audible, while frames containing distinct pulses will generally become more ``smeared out'' in time.
It is not possible in general to satisfy both conditions (1) and (2) simultaneously, but either can be satisfied at the expense of the other. Generally speaking, ``transient frames'' should emphasize condition (2), allowing the WOLA overlap-add cross-fade to take care of the phase discontinuity at the frame boundaries. For stationary segments, phase continuation, preserving condition (1), is more valuable.
It is often sufficient to preserve relative phase across FFT bins (i.e., satisfy condition (2)) only along spectral peaks and their immediate vicinity [142,143,141,138,215,238].
TSM Examples
To illustrate some fundamental points, let's look at some TSM
waveforms for a test signal consisting of two constant-amplitude
sinusoids near 400 Hz having frequencies separated by 10 Hz (to create
an amplitude envelope having 10 beats/sec). We will perform a
![]() time expansion (
time expansion (![]() ``slow-down'') using the following
three algorithms:
``slow-down'') using the following
three algorithms:
- phase-continued vocoder [70]
- relative-phase-preserved vocoder [241,238,143,215]
- SOLA-FS [70,104]11.13
The results are shown in Figures 10.18 through 10.23.
Phase-Continued STFT TSM
Figure 10.18 shows the phase-continued-frames case in which relative phase is not preserved across FFT bins. As a result, the amplitude envelope is not preserved in the time domain within each frame. Figure 10.19 shows the spectrum of the same case, revealing significant distortion products at multiples of the frame rate due to the intra-frame amplitude-envelope distortion, which then ungracefully transitions to the next frame. Note that modulation sidebands corresponding to multiples of the frame rate are common in nonlinearly processed STFTs.
Relative-Phase-Preserving STFT TSM
Figure 10.20 shows the relative-phase-preserving (sometimes called ``phase-locked'') vocoder case in which relative phase is preserved across FFT bins. As a result, the amplitude envelope is preserved very well in each frame, and segues from one frame to the next look much better on the envelope level, but now the individual FFT bin frequencies are phase-modulated from frame to frame. Both plots show the same number of beats per second while the overall duration is doubled in the second plot, as desired. Figure 10.21 shows the corresponding spectrum; instead of distortion-modulation on the scale of the frame rate, the spectral distortion looks more broadband--consistent with phase-discontinuities across the entire spectrum from one frame to the next.
SOLA-FS TSM
Finally, Figures 10.22 and 10.23 show the time and
frequency domain plots for the SOLA-FS algorithm (a time-domain
method). SOLA-type algorithms perform slow-down by repeating frames
locally. (In this case, each frame could be repeated once to
accomplish the ![]() slow-down.) They maximize cross-correlation
at the ``loop-back'' points in order to minimize discontinuity
distortion, but such distortion is always there, though typically
attenuated by a cross-fade on the loop-back. We can see twice as many
``carrier cycles'' under each beat, meaning that the beat frequency
(amplitude envelope) was not preserved, but neither was it severely
distorted in this case. SOLA algorithms tend to work well on speech,
but can ``stutter'' when attack transients happen to be repeated.
SOLA algorithms should be adjusted to avoid repeating a transient
frame; similarly, they should avoid discarding a transient frame when
speeding up.
slow-down.) They maximize cross-correlation
at the ``loop-back'' points in order to minimize discontinuity
distortion, but such distortion is always there, though typically
attenuated by a cross-fade on the loop-back. We can see twice as many
``carrier cycles'' under each beat, meaning that the beat frequency
(amplitude envelope) was not preserved, but neither was it severely
distorted in this case. SOLA algorithms tend to work well on speech,
but can ``stutter'' when attack transients happen to be repeated.
SOLA algorithms should be adjusted to avoid repeating a transient
frame; similarly, they should avoid discarding a transient frame when
speeding up.
Further Reading
For a comprehensive tutorial review of TSM and frequency-scaling techniques, see [138].
Audio demonstrations of TSM and frequency-scaling based on the sines+noise+transients model of Scott Levine [149] may be found online at http://ccrma.stanford.edu/~jos/pdf/SMS.pdf .
See also the Wikipedia page entitled ``Audio time-scale/pitch modification''.
Gaussian Windowed Chirps (Chirplets)
As discussed in §G.8.2, an interesting generalization of sinusoidal modeling is chirplet modeling. A chirplet is defined as a Gaussian-windowed sinusoid, where the sinusoid has a constant amplitude, but its frequency may be linearly ``sweeping.'' This definition arises naturally from the mathematical fact that the Fourier transform of a Gaussian-windowed chirp signal is a complex Gaussian pulse, where a chirp signal is defined as a sinusoid having linearly modulated frequency, i.e., quadratic phase:
| (11.25) |
Applying a Gaussian window to this chirp yields
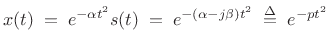 |
(11.26) |
where
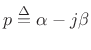 . It is thus clear how naturally
Gaussian amplitude envelopes and linearly frequency-sweeping sinusoids
(chirps) belong together in a unified form called a chirplet.
. It is thus clear how naturally
Gaussian amplitude envelopes and linearly frequency-sweeping sinusoids
(chirps) belong together in a unified form called a chirplet.
The basic chirplet
![]() can be regarded as an
exponential polynomial signal in which the polynomial is of
order 2. Exponential polynomials of higher order have also been
explored [89,90,91].
(See also §G.8.2.)
can be regarded as an
exponential polynomial signal in which the polynomial is of
order 2. Exponential polynomials of higher order have also been
explored [89,90,91].
(See also §G.8.2.)
Chirplet Fourier Transform
The Fourier transform of a complex Gaussian pulse is derived in §D.8 of Appendix D:
This result is valid when
| (11.28) |
we have
| (11.29) |
That is, for
Modulated Gaussian-Windowed Chirp
By the modulation theorem for Fourier transforms,
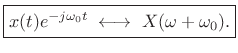 |
(11.30) |
This is proved in §B.6 as the dual of the shift-theorem. It is also evident from inspection of the Fourier transform:
![$\displaystyle \int_{-\infty}^\infty \left[x(t)e^{-j\omega_0 t}\right] e^{-j\omega t} dt \eqsp \int_{-\infty}^\infty x(t)e^{-j(\omega+\omega_0) t} dt \isdefs X(\omega+\omega_0)$](http://www.dsprelated.com/josimages_new/sasp2/img1879.png) |
(11.31) |
Applying the modulation theorem to the Gaussian transform pair above yields
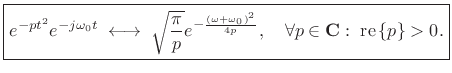 |
(11.32) |
Thus, we frequency-shift a Gaussian chirp in the same way we frequency-shift any signal--by complex modulation (multiplication by a complex sinusoid at the shift-frequency).
Identifying Chirp Rate
Consider again the Fourier transform of a complex Gaussian in (10.27):
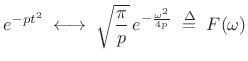 |
(11.33) |
Setting
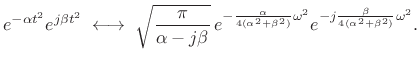 |
(11.34) |
The log magnitude Fourier transform is given by
| (11.35) |
and the phase is
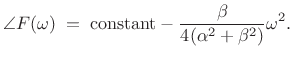 |
(11.36) |
Note that both log-magnitude and (unwrapped) phase are parabolas in
In practice, it is simple to estimate the curvature at a spectral peak using parabolic interpolation:
![\begin{eqnarray*}
c_m &\isdef & \frac{d^2}{d\omega^2} \ln\vert F(\omega)\vert \eqsp - \frac{\alpha}{2(\alpha^2+\beta^2)}\\ [5pt]
c_p &\isdef & \frac{d^2}{d\omega^2} \angle F(\omega) \eqsp - \frac{\beta}{2(\alpha^2+\beta^2)}
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img1886.png)
We can write

Note that the window ``amplitude-rate'' ![]() is always positive.
The ``chirp rate''
is always positive.
The ``chirp rate'' ![]() may be positive (increasing frequency) or
negative (downgoing chirps). For purposes of chirp-rate estimation,
there is no need to find the true spectral peak because the curvature
is the same for all
may be positive (increasing frequency) or
negative (downgoing chirps). For purposes of chirp-rate estimation,
there is no need to find the true spectral peak because the curvature
is the same for all ![]() . However, curvature estimates are
generally more reliable near spectral peaks, where the signal-to-noise
ratio is typically maximum.
In practice, we can form an estimate of
. However, curvature estimates are
generally more reliable near spectral peaks, where the signal-to-noise
ratio is typically maximum.
In practice, we can form an estimate of ![]() from the known FFT
analysis window (typically ``close to Gaussian'').
from the known FFT
analysis window (typically ``close to Gaussian'').
Chirplet Frequency-Rate Estimation
The chirp rate ![]() may be estimated from the relation
may be estimated from the relation
![]() as follows:
as follows:
- Let
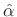 denote the measured (or known) curvature at the
midpoint of the analysis window
denote the measured (or known) curvature at the
midpoint of the analysis window  .
.
- Let
![$ [c_m]$](http://www.dsprelated.com/josimages_new/sasp2/img1890.png) and
and ![$ [c_p]$](http://www.dsprelated.com/josimages_new/sasp2/img1891.png) denote weighted
averages of the measured curvatures
denote weighted
averages of the measured curvatures 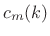 and
and 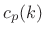 along the log-magnitude and phase of a spectral peak,
respectively.
along the log-magnitude and phase of a spectral peak,
respectively.
- Then the chirp-rate
 estimate may be estimated from the
spectral peak by
estimate may be estimated from the
spectral peak by
![$\displaystyle \zbox {{\hat \beta}\isdefs {\hat \alpha}\frac{[c_p]}{[c_m]}}
$](http://www.dsprelated.com/josimages_new/sasp2/img1894.png)
Simulation Results
Figure 10.24 shows the waveform of a Gaussian-windowed chirp (``chirplet'') generated by the following matlab code:
fs = 8000; x = chirp([0:1/fs:0.1],1000,1,2000); M = length(x); n=(-(M-1)/2:(M-1)/2)'; w = exp(-n.*n./(2*sigma.*sigma)); xw = w(:) .* x(:);
Figure 10.25 shows the same chirplet in a time-frequency plot. Figure 10.26 shows the spectrum of the example chirplet. Note the parabolic fits to dB magnitude and unwrapped phase. We see that phase modeling is most accurate where magnitude is substantial. If the signal were not truncated in the time domain, the parabolic fits would be perfect. Figure 10.27 shows the spectrum of a Gaussian-windowed chirp in which frequency decreases from 1 kHz to 500 Hz. Note how the curvature of the phase at the peak has changed sign.
FFT Filter Banks
This section, based on [265], describes how to make practical audio filter banks using the Short Time Fourier Transform (STFT). This material bridges the filter-bank interpretation of the STFT in Chapter 9 and the discussion of multirate filter banks in Chapter 11. The filter banks of this section are based entirely on the STFT, with consideration of the basic Fourier theorems introduced in Chapter 2. In Chapter 11, filter banks such as used in audio compression are addressed. However, when not doing compression, i.e., when each channel of the filter bank does not have to be critically sampled, the methods of this section may suffice in many applications.
Audio Filter Banks
It is well known that the frequency resolution of human hearing decreases with frequency [71,276]. As a result, any ``auditory filter bank'' must be a nonuniform filter bank in which the channel bandwidths increase with frequency over most of the spectrum. A classic approximate example is the third-octave filter bank.11.14 A simpler (cruder) approximation is the octave filter bank,11.15 also called a dyadic filter bank when implemented using a binary tree structure [287]. Both are examples of constant-Q filter banks [29,30,244], in which the bandwidth of each filter-bank channel is proportional to center frequency [263]. Approximate auditory filter banks, such as constant-Q filter banks, have extensive applications in computer music, audio engineering, and basic hearing research.
If the output signals from all channels of a constant-Q filter bank are all sampled at a particular time, we obtain what may be called a constant-Q transform [29]. A constant-Q transform can be efficiently implemented by smoothing the output of a Fast Fourier Transform (FFT) [30]. More generally, a multiresolution spectrogram can be implemented by combining FFTs of different lengths and advancing the FFTs forward through time (§7.3). Such nonuniform filter banks can also be implemented based on the Goetzel algorithm [33].
While the topic of filter banks is well developed in the literature, including constant-Q, nonuniform FFT-based, and wavelet filter banks, the simple, robust methods presented in this section appear to be new [265]. In particular, classic nonuniform FFT filter banks as described in [226] have not offered the perfect reconstruction property [287] in which the filter-bank sum yields the input signal exactly (to within a delay and/or scale factor) when the filter-band signals are not modified. The voluminous literature on perfect-reconstruction filter banks [287] addresses nonuniform filter banks, such as dyadic filter banks designed based on pseudo quadrature mirror filter designs, but simpler STFT methods do not yet appear to be incorporated. In the cosine-modulated filter-bank domain, subband DCTs have been used in a related way [302], but apparently without consideration for the possibility of a common time domain across multiple channels.11.16
This section can be viewed as an extension of [30] to the FFT filter-bank case. Alternatively, it may be viewed as a novel method for nonuniform FIR filter-bank design and implementation, based on STFT methodology, with arbitrarily accurate reconstruction and controlled aliasing in the downsampled case. While we consider only auditory (approximately constant-Q) filter banks, the method works equally well for arbitrary nonuniform spectral partitions and overlap-add decompositions in the frequency domain.
Basic Idea
The basic idea is to partition FFT bins into the desired nonuniform bands, and perform smaller inverse FFTs on each subband to synthesize downsampled time-domain signals in each band. A simple example for a length 8 FFT octave filter bank is shown in Fig.10.30. We'll next extend this example to a practically useful level via a series of tutorially oriented matlab examples.
![\includegraphics[width=0.8\twidth]{eps/fft8}](http://www.dsprelated.com/josimages_new/sasp2/img1901.png) |
Summing STFT Bins
In the Short-Time Fourier Transform, which implements a uniform FIR filter bank (Chapter 9), each FFT bin can be regarded as one sample of the filter-bank output in one channel. It is elementary that summing adjacent filter-bank signals sums the corresponding pass-bands to create a wider pass-band. Summing adjacent FFT bins in the STFT, therefore, synthesizes one sample from a wider pass-band implemented using an FFT. This is essentially how a constant-Q transform is created from an FFT in [30] (using a different frequency-weighting, or ``smoothing kernel''). However, when making a filter bank, as opposed to only a transform used for spectrographic purposes, we must be able to step the FFT through time and compute properly sampled time-domain filter-bank signals.
The wider pass-band created by adjacent-channel summing requires a higher sampling rate in the time domain to avoid aliasing. As a result, the maximum STFT ``hop size'' is limited by the widest pass-band in the filter bank. For audio filter banks, low-frequency channels have narrow bandwidths, while high-frequency channels are wider, thereby forcing a smaller hop size for the STFT. This means that the low-frequency channels are heavily oversampled when the high-frequency channels are merely adequately sampled (in time) [30,88]. In an octave filter-bank, for example, the top octave, occupying the entire upper half of the spectrum, requires a time-domain step-size of no more than two samples, if aliasing of the band is to be avoided. Each octave down is then oversampled (in time) by an additional factor of 2.
Inverse Transforming STFT Bin Groups
The solution proposed in [265] is to compute
multiple time samples for each high-frequency channel, so that
one hop of the FFT produces all needed samples in each band. That way
all channels can use the same hop-size without redundancy. If the
narrowest band gets one sample per hop, then a band ![]() times as wide
must produce
times as wide
must produce ![]() samples per hop.
samples per hop.
A fast way to compute multiple time samples from the frequency-samples (FFT bins) of a given band is an inverse FFT, as shown in Fig.10.30. In matlab notation, let X(1:N) denote the FFT (length N) of the current frame of data in the STFT, and denote the lower and upper spectral samples for band k by lsn(k) and hsn(k), respectively. Then we may specify the matlab computation of the full-rate time-domain signal corresponding to band k as follows:
BandK = X(lsn(k):hsn(k)); z1 = zeros(1,lsn(k)-1); z2 = zeros(1,N-hsn(k)); BandKzp = [z1, BandK, z2]; % (1) x(k,:) = ifft(BandKzp);where x(k,:) denotes the output signal vector (length N) for the kth filter-bank channel for the current time-domain STFT window.
Let
![]() denote the number of
FFT bins in band
denote the number of
FFT bins in band ![]() . When
. When
![]() is a power of 2, we can apply an
inverse FFT only to the nonzero samples in the band:
is a power of 2, we can apply an
inverse FFT only to the nonzero samples in the band:
xd{k} = ifft(BandK);
where xd{k} now denotes a cell array for holding the
``downsampled'' signal vectors (since the downsampling factor is
typically different for different bands).
We may relate x(k,:) and xd{k} by noting that, when Lk = N/Nk is an integer, we have that the relation
BandK == alias(BandKzp,Lk) % (2)is true, for each element, where alias(x,K) denotes aliasing of K equal partitions of the vector x (§2.3.12):11.17
function y = alias(x,L)
Nx = length(x);
Np = Nx/L; % aliasing-partition length
x = x(:); % ensure column vector
y = zeros(Np,1);
for i=1:L
y = y + x(1+(i-1)*Np : i*Np);
end
By the aliasing theorem (downsampling theorem) for Discrete Fourier Transforms (DFTs) (§2.3.12), the relation (2) in the frequency domain corresponds to
xd{k} == Lk * x(k,1:Lk:end)
in the time domain, i.e., xd{k} is obtained from x(k,:) by
means of downsampling by the factor Lk. This produces
N/Lk == Nk samples. That is, for a band that is Nk bins wide,
we obtain Nk time-domain samples for each STFT frame, when critically
sampled. (At the full rate, we obtain N samples from each channel
for each frame.)
We see that taking an inverse FFT of only the bins in a given channel computes the critically downsampled signal for that channel. Downsampling factors between 1 and Lk can be implemented by choosing a zero-padding factor for the band somewhere between 1 and Lk samples.
Note that this filter bank has the perfect reconstruction (PR) property [287]. That is, the original input signal can be exactly reconstructed (to within a delay and possible scale factor) from the channel signals. The PR property follows immediately from the exact invertibility of the discrete Fourier transform. Specifically, we can recover the original signal frame by taking an FFT of each channel-signal frame and abutting the spectral bins so computed to form the original frame spectrum. Of course, the underlying STFT (uniform filter bank) must be PR as well, as it routinely is in practice.
Improving the Channel Filters
Recall that each FFT bin can be viewed as a sample from a bandpass filter whose frequency response is a frequency-shift of the FFT-window Fourier transform (§9.3). Therefore, the frequency response of a channel filter obtained by summing Nk adjacent FFT bins is given by the sum of Nk window transforms, one for each FFT bin in the sum. As a result, the stop-band of the channel-filter frequency response is a sum of Nk window side lobes, and by controlling window side-lobe level, we may control the stop-band gain of the channel filters.
The transition width from pass-band to stop-band, on the other hand, is given by the main-lobe width of the window transform (§5.5.1). In the previous subsection, by zero-padding the band (line (1) above), we implicitly assumed a transition width of one bin. Only the length N rectangular window can be reasonably said to have a one-bin transition from pass-band to stop-band. Since the first side lobe of a rectangular window transform is only about 13 dB below the main lobe, the rectangular window gives poor stop-band performance, as illustrated in Fig.10.33. Moreover, we often need FFT data windows to be shorter than the FFT size N (i.e., we often need zero-padding in the time domain) so that the frame spectrum will be oversampled, enabling various spectral processing such as linear filtering (Chapter 8).
One might wonder how the length N rectangular window can be all that bad when it gives the perfect reconstruction property, as demonstrated in the previous subsection. The answer is that there is a lot of aliasing in the channel signals, when downsampled, but this aliasing is exactly canceled in the reconstruction, provided the channel signals were not modified in any way.
Going back to §10.7.3, we need to replace the zero-padded band (1) by a proper filtering operation in the frequency domain (a ``spectral window''):
BandK2 = Hk .* X;
x(k,:) = ifft(BandK2); % full rate
BandK2a = alias(BandK2,Nk);
xd{k} = ifft(BandK2a); % crit samp
where the channel filter frequency response Hk may be prepared in
advance as the appropriate weighted sum of FFT-window transforms:Hideal = [z1,ones(1,Nk),z2]; Hk = cconvr(W,Hideal); % circ. conv.where z1 and z2 are the same zero vectors defined in §10.7.3, and cconvr(W,H) denotes the circular convolution of two real vectors having the same length [264]:
function [Y] = cconvr(W,X) wc=fft(W); xc=fft(X); yc = wc .* xc; Y = real(ifft(yc));Note that in this more practical case, the perfect reconstruction property no longer holds, since the operation
BandK2a = alias(Hk .* X, Nk);is not exactly invertible in general.11.18However, we may approach perfect reconstruction arbitrarily closely by only aliasing stop-band intervals onto the pass-band, and by increasing the stop-band attenuation of Hk as desired. In contrast to the PR case, we do not rely on aliasing cancellation, which is valuable when the channel signals are to be modified.
The band filters Hk can be said to have been designed by the window method for FIR filter design [224]. (See functions fir1 and fir2 in Octave and/or the Matlab Signal Processing Toolbox.)
Fast Octave Filter Banks
Let's now apply the above technique to the design of an octave filter bank.11.19 At first sight, this appears to be a natural fit, because it is immediately easy to partition a power of 2 (typical for the FFT size N) into octaves, each having a width in bins that is a power of 2. For example, when N == 8, we have the following stack of frequency-response vectors for the rectangular-window, no-zero-padding, complex-signal case:
H = [ ... 0 0 0 0 1 1 1 1 ; ... 0 0 1 1 0 0 0 0 ; ... 0 1 0 0 0 0 0 0 ; ... 1 0 0 0 0 0 0 0 ];Figure 10.31 depicts the resulting filter bank schematically in the frequency domain.11.20 Thus, H(1,:) is the frequency-response for the top (first) octave, H(2,:) is the frequency-response for the next-to-top (second) octave, H(3,:) is the next octave down, and H(4,:) is the ``remainder'' of the spectrum. (In every octave filter bank, there is a final low-frequency band.
A schematic of the filter-bank implementation using FFTs is shown in Fig.10.30. The division by N called for by ifft(N) is often spread out among the ifft butterfly stages as divisions by 2 (one-bit right-shifts in fixed-point arithmetic) after each of them. For conservation of dynamic range, half of the right-shifts can be spread out among every other forward-FFT butterfly stage [28] as well.
The simple spectral partitioning of Fig.10.31 is appropriate for complex signals--those for which the spectrum is regarded as spanning 0 Hz to the sampling rate. For real signals, we need a spectral partition more like that in Fig.10.32.
Unfortunately, the number of spectral samples in Fig.10.32 is 14--not a power of 2. (The previous length 8 complex case maps to length 14 real case because the dc and Nyquist-limit samples do not have complex-conjugate counterparts.) Discarding the sample at the Nyquist limit--number 8 in Fig.10.32--does not help, since that gives 13 samples--still not a power of 2. In summary, there is no obvious way to octave-partition the spectral samples of a real signal while maintaining the power-of-2 condition for each band and symmetrically partitioning positive and negative frequencies.
A real signal can of course be converted to its corresponding ``analytic signal'' by filtering out the negative-frequency components. This is normally done by designing a Hilbert transform filter [133,224]. However, such filters are large-order FIR filters, exactly like we are trying to design! If we design our filter bank properly, we can use it to zero the negative-frequency components.
Spectral Rotation of Real Signals
Note that if we rotate the spectrum of a real signal by half a
bin, we obtain ![]() positive-frequency samples and
positive-frequency samples and ![]() negative-frequency samples, with no sample at dc or at the Nyquist
limit. This is typically desirable for audio signals because dc is
inaudible and the Nyquist limit is a degenerate point of the spectrum
that, for example, cannot have a phase other than 0 or
negative-frequency samples, with no sample at dc or at the Nyquist
limit. This is typically desirable for audio signals because dc is
inaudible and the Nyquist limit is a degenerate point of the spectrum
that, for example, cannot have a phase other than 0 or ![]() . If
. If ![]() is a power of 2, then so is
is a power of 2, then so is ![]() , and the octave-band partitioning of
the previous subsection can be applied separately to each half of the
spectrum:
, and the octave-band partitioning of
the previous subsection can be applied separately to each half of the
spectrum:
N = 32; x = randn(1,N); % Specific example LN = round(log2(N)); % number of octave bands shifter = exp(-j*pi*[0:N-1]/N); % half-bin xs = x .* shifter; % apply spectral shift X = fft(xs,N); % project xs onto rotated basis XP = X(1:N/2); % positive-frequency components XN = X(N:-1:N/2+1); % neg.-frequency components YP = dcells(XP); % partition to octave bands YN = dcells(XN); % ditto for neg. frequencies YPe = dcells2spec(YP); % unpack "dyadic cells" YNe = dcells2spec(YN); % unpack neg. freqs YNeflr = fliplr(YNe); % undo former flip ys = ifft([YPe,YNeflr],N,2); y = real(ones(LN,1)*conj(shifter) .* ys); % = octave filter-bank signals (real) yr = sum(y); % filter-bank sum (should equal x) yrerr = x - yr; disp(sprintf(... 'Total filter-bank sum L2 error = %0.2f %%',... 100*norm(yrerr)/norm(x)));In the above listing, the function dcells11.21simply forms a cell array in matlab containing the spectral partition (``dyadic cells''). The function dcells2spec11.22is the inverse of dcells, taking a spectral partition and unpacking it to produce a usual spectrum vector.
Improving the Octave Band Filters
To see the true filter-bank frequency response corresponding to Fig.10.31, we may feed an impulse to the filter bank and take a long FFT (for zero padding) of the channel signals to produce the interpolated response shown in Fig.10.33.
The horizontal line along 0 dB in Fig.10.33 was obtained by summing the channel responses, indicating that it is a perfect-reconstruction filter-bank, as expected. However, the stop-band performance of the channels is quite poor, being comparable to the side-lobes of a rectangular window transform (an aliased sinc function). In fact, the stop-band is identical to the rectangular-window side-lobes for the two lowest bands. Notice that the original eight samples of Fig.10.31 still lie along the 0-dB line, and there are still zeros in each channel response beneath the unity-gain point of every other channel's response, so Fig.10.31 can be obtained by sampling Fig.10.33 at those eight points. However, the interpolated response shows that the filter bank is quite poor by audio standards.
![\includegraphics[width=0.8\twidth]{eps/impulse-cheb127h-rect129x-N256-partition-interp}](http://www.dsprelated.com/josimages_new/sasp2/img1908.png) |
Figure 10.34 shows an octave filter bank (again for complex signals) that is better designed for audio usage. Instead of basing the channel filter prototype on the rectangular window, a Dolph-Chebyshev window was used (using the matlab function call chebwin(127,80)). The FFT size is about twice the filter length, thereby allowing for a data frame of equal length (to the filter) without incurring time aliasing, in the usual way for STFTs (Chapter 8). The data window is chosen to overlap-add to a constant, as typical in STFTs, so its choice does not affect the quality of the filter-bank output channel signals. We therefore may continue to use a rectangular data window that advances by its full length each frame. Choosing an odd filter length facilitates zero-phase offline STFT processing, in which the middle FIR sample is treated as occurring at time zero, so that there is no delay in any filter-bank channel [264].
The filter bank is PR in the full-rate case because the underlying STFT is PR, in the absence of modifications, and because the channel filter-bank is constant-overlap-add in the frequency domain (again in the absence of modifications) according to STFT theory (Chapter 8).
Aliasing on Downsampling
While the filter bank of Fig.10.34 gives good stop-band rejection, there is still a significant amount of aliasing when the bands are critically sampled. This happens because the transition bands are aliased about their midpoints. This can be seen in Fig.10.34 by noting that aliasing ``folding frequencies'' lie at the crossover point between each pair of bands. An overlay of the spectra of the downsampled filter-bank outputs, for an impulse input, is shown in Fig.10.35.
![\includegraphics[width=0.8\twidth]{eps/impulse-cheb127h-rect129x-N256-aliased-partition-interp}](http://www.dsprelated.com/josimages_new/sasp2/img1909.png) |
Figure 10.36 shows the aliased spectral signal bands (prior to inverse STFT) for a step input (same filter bank). (This type of plot looks ideal for an impulse input signal because the spectrum is constant, so the aliased bands are also constant.) Note the large slice of dc energy that has aliased from near the sampling rate to near half the sampling rate in the top octave band. The signal and error spectra are shown overlaid in Fig.10.37. In this case, the aliasing causes significant error in the reconstruction.
![\includegraphics[width=0.8\twidth]{eps/step-cheb127h-rect129x-N256-aliased-error-interp}](http://www.dsprelated.com/josimages_new/sasp2/img1911.png) |
Restricting Aliasing to Stop-Bands
To eliminate the relatively heavy transition-band aliasing (when
critically sampling the channel signals), we can define
overlapping bands such that each band encompasses the
transition bands on either side. However, unless a full
![]() oversampling is provided for each band (which is one easy solution),
the bandwidth (in bins) is no longer a power of two, thereby thwarting
use of radix-2
inverse-FFTs to compute the
time-domain band signals.
oversampling is provided for each band (which is one easy solution),
the bandwidth (in bins) is no longer a power of two, thereby thwarting
use of radix-2
inverse-FFTs to compute the
time-domain band signals.
To keep the channel bandwidths at powers of two while restricting aliasing to stop-band energy, the IFFT bands can be widened to include transition bands on either side. That is, the desired pass-band plus the two transition bands span a power-of-two bins. This results in overlapping channel IFFTs. Figure 10.38 shows how the example of Fig.10.34 is modified by this strategy.
![\includegraphics[width=0.8\twidth]{eps/impulse-cheb127h-rect128x-N256-qdcells}](http://www.dsprelated.com/josimages_new/sasp2/img1913.png) |
The basic principle of filter-bank band allocation is to enclose each filter band plus its transition bands within a wider band that is a power-of-two bins wide.11.23 The band should roll off to reach its stop-band at the edge of the wider encompassing band. It is fine to have extra space in the wider band, and this may be filled with a continuation of the enclosed band's stop-band response (or some tapering of it--since we assume stop-band energy is negligible, the difference should be inconsequential). The desired bands may overlap each other by any amount, and may have any desired shape. The encompassing bands then overlap further to reach the next power of two (in width) for each overlapping extended band. (See the gammatone and gammachirp filter banks for examples of heavily overlapping bands in an audio filter bank [111].)
In this approach, pass-bands of arbitrary width are embedded in overlapping IFFT bands that are a power-of-2 wide. As a result of this flexibility, the frequency-rotation trick of §10.7.7 is no longer needed for real filter banks. Instead, we simply allocate any desired bands between dc and half the sampling rate, and then conjugate-symmetry dictates the rest. In addition to a left-over ``dc-Nyquist'' band, there is a similar residual ``Nyquist-limit'' band (a typically negligible band about half the sampling rate). In other words, since the pass-bands may be any width and the encompassing IFFT bands may overlap by any amount, they do not have to ``pack'' conveniently as power-of-two blocks.
The minimum channel bandwidth is defined as two transition bands plus one bin (i.e., the minimum pass-band width is zero, corresponding to one bin, or one spectral sample). For the Dolph-Chebyshev window, the transition bandwidth is known in closed form [155]. In our examples, we have a length 127 window with 80 dB stop-band attenuation in the lowpass prototype [chebwin(127,80)], corresponding to a transition width of 6.35 bins in a length 256 FFT, which was rounded up to 7 bins in software for simplicity of band allocation. Therefore, our minimum channel bandwidth is 15 bins (two transition bands plus one sample for the band center). The next highest power of two is 16, so that is our minimum encompassing IFFT length for any band.
The dc and Nyquist channels are combined into a single channel containing the left-over residual filter-bank response consisting of a low transition down from dc and a high-frequency transition up to the sampling rate (in the complex-signal case). When N is sufficiently large so that these bands contain no audible energy, they may be discarded. We include them in all examples here so as to preserve the (near) perfect reconstruction property of the filter bank. Thus, the 7-bin dc channel is combined with the 7-bin Nyquist channel to form a single 16-bin encompassing residual band that may be discarded in many audio applications (when the initial FFT size is sufficiently large for the sampling rate used).
In the example of Fig.10.38, the
initial FFT size is 256, and the channel bandwidths (pass-bands only,
excluding transitions), from top to
bottom, are 121, 64, 32, 16, and 8 bins. The top band is reduced by 7
bins to leave a transition band to the sampling rate. Similarly, the
lowest band lies above a transition band consisting of bins 0-6. The
encompassing IFFTs (containing transitions) are lengths 256, 128, 64, 32, 32, for the interior
bands, and a length 32 IFFT handles the dc and Nyquist bands (which
are combined into a single 14-bin band about dc, which occupies 28
bins when the transition bands are appended). Letting [lo,hi] denote a
band by its lower and upper bin limit, the non-overlapping adjacent
pass-band edges in ``spectral samples''11.24 of the interior bands are [8, 15],
[16, 31], [32, 63], [64, 127], and [128, 248]; the overlapping
encompassing IFFT band edges are then [1, 32], [9, 40], [25, 88], [57,
184], [1, 256], i.e., they each contain a pass-band and two transition
bands, and have a power-of-2 length. The downsampling factor for each
channel can be computed as the initial FFT size (256) divided by the
IFFT size (![]() ,
, ![]() ,
, ![]() ,
, ![]() , or
, or ![]() ) for the channel.
) for the channel.
Figure 10.39 shows the counterpart of Fig.10.35 for this example. In this case, the aliased signal energy comes only from channel-filter stop-bands. For narrow bands, the aliasing is suppressed by at least 80 dB (the side-lobe level of the chosen Dolph-Chebyshev window transform). For bands significantly wider than one bin (the minimum bandwidth in this example is the dc-Nyquist band at 14 bins), the stop-band consists of a sum of shifts of the window-transform side lobes, and these are found to be more than 80 dB down due to cancellation (more than 90 dB down in most bands of this example).
![\includegraphics[width=0.8\twidth]{eps/impulse-cheb127h-rect128x-N256-aliased-qdcells}](http://www.dsprelated.com/josimages_new/sasp2/img1918.png) |
Tightening the IFFTs
In this example the top band is not downsampled at all, and
the interior bands are oversampled by approximately 2. This is because
the desired pass-band widths started out at a power of 2, so that the
addition of transition bands forced the next higher power of 2 for the
IFFT size. Narrowing the width of the top band from 121 bins to
![]() bins would enable use of a length 128 IFFT for
the top band, and similarly for the lower bands. In other words, when
the desired spectral partition is that of an ideal octave filter bank,
as sketched in Fig.10.31, narrowing each octave-band by
twice the transition width of the lowpass prototype filter (and
``covering down'' to keep them adjacent) will produce a relatively
``tight'' FFT filterbank design in which the IFFT sizes remain the
same length as in the heavily aliased case discussed above
(Fig.10.35).
When applied to the octave filter bank, the pass-bands become a little
narrower than one octave. We may call this a quasi octave
filter bank.
bins would enable use of a length 128 IFFT for
the top band, and similarly for the lower bands. In other words, when
the desired spectral partition is that of an ideal octave filter bank,
as sketched in Fig.10.31, narrowing each octave-band by
twice the transition width of the lowpass prototype filter (and
``covering down'' to keep them adjacent) will produce a relatively
``tight'' FFT filterbank design in which the IFFT sizes remain the
same length as in the heavily aliased case discussed above
(Fig.10.35).
When applied to the octave filter bank, the pass-bands become a little
narrower than one octave. We may call this a quasi octave
filter bank.
Real Filter Bank Example
Finally, Fig.10.40 shows the appearance of the octave filter bank for real signals. In this case, bands are constructed between dc and half the sampling rate, and conjugate symmetry is used to automatically construct the desired bands between half the sampling rate and the sampling rate. The band allocation algorithm therefore needs no modification for the real-signal case.
![\includegraphics[width=0.8\twidth]{eps/impulse-cheb127h-rect128x-N256-real-qdcells}](http://www.dsprelated.com/josimages_new/sasp2/img1920.png) |
Optimal Band Filters
In the filter-bank literature, one class of filter banks is called ``cosine modulated'' filter banks. DFT filter banks are similar. The lowpass-filter prototype in such filter banks can be used in place of the Dolph-Chebyshev window used here. Therefore, any result on optimal design of cosine-modulated filter banks can be adapted to this context. See, for example, [253,302]. Note, however, that in principle a separate optimization is needed for each different channel bandwidth. An optimal lowpass prototype only optimizes channels having a one-bin pass-band, since the prototype frequency-response is merely shifted in frequency (cosine-modulated in time) to create the channel frequency response. Wider channels are made by summing such channel responses, which alters the stop-bands.
In practice, the Dolph-Chebyshev window, used in the examples of this section, typically yields a filter bank magnitude frequency response that is optimal in the Chebyshev sense, when at least one channel is minimum width, because
- there can be only one lowpass prototype filter in any modulated filter bank (such as the DFT filter bank),
- the prototype itself is the optimal Chebyshev lowpass filter of minimum bandwidth, and
- summing shifted copies of the prototype frequency response (to synthesize a wider pass-band) generally improves the stop-band rejection over that of the prototype, thereby meeting the Chebyshev optimality requirement for the filter-bank as a whole (keeping below the worst-case deviation of the prototype).
The Dolph-Chebyshev window has faint impulsive endpoints on the order of the side-lobe level (about 50 dB down in the 80-dB-SBA examples above), and in some applications, this could be considered an undesirable time-domain characteristic. To eliminate them, an optimal Chebyshev window may be designed by means of linear programming with a time-domain monotonicity constraint (§3.13). Alternatively, of course, other windows can be used, such as the Kaiser, or three-term Blackman-Harris window, to name just two (Chapter 3).
FFT Filter-Bank Summary and Fourier Duality with OLA
We have seen in this section how to make general FIR filter banks implemented using the STFT. This approach can be seen as the Fourier dual of time-domain overlap-add (OLA) STFT processing (Chapter 8).
To summarize in terms of OLA duality, we perform any desired overlap-add decomposition of the spectrum of an STFT frame in the frequency domain. Each STFT spectrum is multiplied, in the frequency domain, by a time-limited spectral window (i.e., an FIR-filter frequency-response). To obtain FFT efficiency for arbitrary spectral bands, we extend the width each spectral band (either zero-padding or ``stop-band-padding'') to the next power of 2; this is reminiscent of the OLA step of zero-padding a time-domain frame to the next power of 2. An inverse FFT is performed on the extended band, either in its natural location, or translated to baseband. For the channel signals to have a common sampling rate, each band is embedded in the same spectral domain from dc to half the common sampling rate (or the full sampling rate in the complex case), and the same-length IFFT is used for each spectral band. On the other hand, when the channel signals are downsampled to their natural bandwidths (rounded up to the next power of 2 in FFT bins), the aliasing distortion is fully controlled by the stop-band rejection of the band-filter used.
Pointers to Sound Examples
See the CCRMA Music 421 website for pointers to demonstrations and sound examples related to applications of the STFT. A PDF presentation including pointers to a good number of sound examples can be found at the author's website.11.25
Next Section:
Multirate Filter Banks
Previous Section:
The Filter Bank Summation (FBS) Interpretation of the Short Time Fourier Transform (STFT)








![$\displaystyle \arg\max_{{\hat f}_0} \sum_{k=1}^K
\log\left[\left\vert X(k{\hat f}_0)\right\vert+\epsilon\right]$](http://www.dsprelated.com/josimages_new/sasp2/img1721.png)
![$\displaystyle \arg\max_{{\hat f}_0} \prod_{k=1}^K \left[\left\vert X(k{\hat f}_0)\right\vert+\epsilon\right]
\protect$](http://www.dsprelated.com/josimages_new/sasp2/img1722.png)
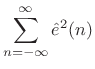
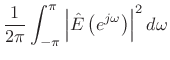
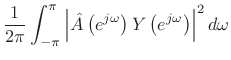
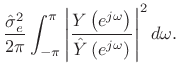
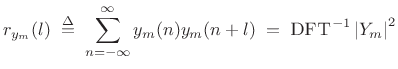
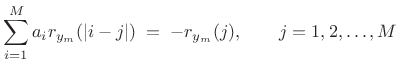
![\includegraphics[width=\textwidth ]{eps/ImpulseTrain}](http://www.dsprelated.com/josimages_new/sasp2/img1783.png)
![\includegraphics[width=\textwidth ]{eps/Speech}](http://www.dsprelated.com/josimages_new/sasp2/img1784.png)
![\includegraphics[width=\textwidth ]{eps/CepstrumBoxcar}](http://www.dsprelated.com/josimages_new/sasp2/img1785.png)
![\includegraphics[width=\textwidth ]{eps/CepstrumEnvBoxcarC}](http://www.dsprelated.com/josimages_new/sasp2/img1786.png)
![\includegraphics[width=\textwidth ]{eps/CepstrumEnvHanningC}](http://www.dsprelated.com/josimages_new/sasp2/img1787.png)
![\includegraphics[width=\textwidth ]{eps/LinearPredictionEnvC}](http://www.dsprelated.com/josimages_new/sasp2/img1788.png)
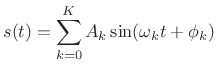
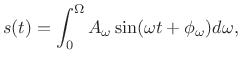
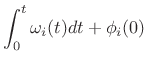
![\begin{psfrags}
% latex2html id marker 27324\psfrag{A1} []{ \Large$ A_1(t)$\ }\psfrag{A2} []{ \Large$ A_2(t)$\ }\psfrag{A3} []{ \Large$ A_3(t)$\ }\psfrag{A4} []{ \Large$ A_4(t)$\ }\psfrag{f1} []{ \Large$ f_1(t)$\ }\psfrag{f2} []{ \Large$ f_2(t)$\ }\psfrag{f3} []{ \Large$ f_3(t)$\ }\psfrag{f4} []{ \Large$ f_4(t)$\ }\psfrag{s} [b]{ {\Huge$\sum$} }\psfrag{noise} [][b]{{\Large$\stackrel{\hbox{[new] noise}}{u(t)}$}}\psfrag{Filter} [][c]{{\Large$\stackrel{\hbox{filter}}{h_t(\tau)}$}}\psfrag{out} []{
{\large$ y(t)= \sum\limits_{i=1}^{4}
A_i(t)\sin\left[\int_0^t\omega_i(t)dt +\phi_i(0)\right]
+ (h_t \ast u)(t) $\ = sine-sum + filtered-noise}}\begin{figure}[htbp]
\includegraphics[width=0.9\twidth]{eps/additive}
\caption{Sinusoidal oscillator bank and filtered
noise for sines+noise spectral modeling synthesis.}
\end{figure}
\end{psfrags}](http://www.dsprelated.com/josimages_new/sasp2/img1810.png)
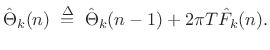
![\includegraphics[width=0.8\twidth]{eps/peak}](http://www.dsprelated.com/josimages_new/sasp2/img1826.png)
![\includegraphics[width=0.8\twidth]{eps/tracks}](http://www.dsprelated.com/josimages_new/sasp2/img1828.png)
![\begin{psfrags}
% latex2html id marker 27619\psfrag{s} []{\Large$s(t)$}\psfrag{tan} []{\Large$\tan^{-1}$}\begin{figure}[htbp]
\includegraphics[width=\twidth]{eps/analysis}
\caption{Block diagram
of a sinusoidal-modeling \emph{analysis} system
(from \cite{SerraT}).}
\end{figure}
\end{psfrags}](http://www.dsprelated.com/josimages_new/sasp2/img1829.png)
![\begin{psfrags}
% latex2html id marker 27835\psfrag{s}{\Large $x(n)$}\begin{figure}[htbp]
\includegraphics[width=\twidth]{eps/smsanal}
\caption{Sines+noise analysis diagram
(from \cite{SerraT}).}
\end{figure}
\end{psfrags}](http://www.dsprelated.com/josimages_new/sasp2/img1839.png)
![\begin{psfrags}
% latex2html id marker 27855\psfrag{IFFT} [][c]{{\Large IFFT $\cdot w$}}\begin{figure}[htbp]
\includegraphics[width=\twidth]{eps/smssynth}
\caption{Sines+noise synthesis diagram
(from \cite{SerraT}).}
\end{figure}
\end{psfrags}](http://www.dsprelated.com/josimages_new/sasp2/img1842.png)
![\includegraphics[width=0.9\twidth]{eps/scottl-tf-aac}](http://www.dsprelated.com/josimages_new/sasp2/img1847.png)
![\includegraphics[width=0.9\twidth]{eps/scottl-tf-smooth}](http://www.dsprelated.com/josimages_new/sasp2/img1848.png)
![\includegraphics[width=0.9\twidth]{eps/scottl-bark-noise}](http://www.dsprelated.com/josimages_new/sasp2/img1849.png)
![\includegraphics[width=0.9\twidth]{eps/scottl-noise-env}](http://www.dsprelated.com/josimages_new/sasp2/img1850.png)
![\includegraphics[width=0.9\twidth]{eps/scottl-time-scale}](http://www.dsprelated.com/josimages_new/sasp2/img1853.png)
![\includegraphics[width=\twidth]{eps/pv-ellis-wave}](http://www.dsprelated.com/josimages_new/sasp2/img1864.png)
![\includegraphics[width=\twidth]{eps/pv-ellis-spec}](http://www.dsprelated.com/josimages_new/sasp2/img1865.png)
![\includegraphics[width=\twidth]{eps/pv-salsman-wave}](http://www.dsprelated.com/josimages_new/sasp2/img1866.png)
![\includegraphics[width=\twidth]{eps/pv-salsman-spec}](http://www.dsprelated.com/josimages_new/sasp2/img1867.png)
![\includegraphics[width=\twidth]{eps/pv-solafs-wave}](http://www.dsprelated.com/josimages_new/sasp2/img1868.png)
![\includegraphics[width=\twidth]{eps/pv-solafs-spec}](http://www.dsprelated.com/josimages_new/sasp2/img1869.png)
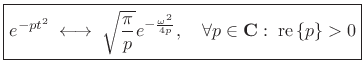
![\includegraphics[width=\twidth]{eps/gwchirp}](http://www.dsprelated.com/josimages_new/sasp2/img1895.png)
![\includegraphics[width=\twidth]{eps/gwchirpsgC}](http://www.dsprelated.com/josimages_new/sasp2/img1896.png)
![\includegraphics[width=\twidth]{eps/gwchirpxform}](http://www.dsprelated.com/josimages_new/sasp2/img1897.png)
![\includegraphics[width=\twidth]{eps/gwchirpdownxform}](http://www.dsprelated.com/josimages_new/sasp2/img1898.png)
![\includegraphics[width=\twidth,height=3in]{eps/gwchirpshort}](http://www.dsprelated.com/josimages_new/sasp2/img1899.png)
![\includegraphics[width=\twidth]{eps/gwchirpshortxform}](http://www.dsprelated.com/josimages_new/sasp2/img1900.png)
![\includegraphics[width=0.8\twidth]{eps/simple-partition}](http://www.dsprelated.com/josimages_new/sasp2/img1904.png)
![\includegraphics[width=0.8\twidth]{eps/simple-real-partition}](http://www.dsprelated.com/josimages_new/sasp2/img1905.png)
![\includegraphics[width=0.8\twidth]{eps/simple-partition-interp}](http://www.dsprelated.com/josimages_new/sasp2/img1907.png)
![\includegraphics[width=0.8\twidth]{eps/step-cheb127h-rect129x-N256-aliased-unpacked}](http://www.dsprelated.com/josimages_new/sasp2/img1910.png)











