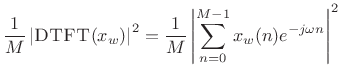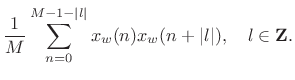Free Books
   Free Books    Spectral Audio Signal Processing  

The Periodogram

The periodogram is based on the definition of the power spectral density (PSD) (see Appendix C). Let $ x_w(n) = w(n)x(n)$ denote a windowed segment of samples from a random process $ x(n)$ , where the window function $ w$ (classically the rectangular window) contains $ M$ nonzero samples. Then the periodogram is defined as the squared-magnitude DTFT of $ x_w$ divided by $ M$ [120, p. 65]:7.7

$\displaystyle P_{x,M}(\omega)$ $\displaystyle \isdef$ $\displaystyle \frac{1}{M} \left\vert\hbox{\sc DTFT}(x_w)\right\vert^2 = \frac{1}{M} \left\vert\sum_{n=0}^{M-1} x_w(n)e^{-j\omega n}\right\vert^2 \protect$ (7.23)
  $\displaystyle \longleftrightarrow$ $\displaystyle \frac{1}{M} \sum_{n=0}^{M-1-\vert l\vert} x_w(n)x_w(n+\vert l\vert), \quad l\in{\bf Z}.$  

In the limit as $ M$ goes to infinity, the expected value of the periodogram equals the true power spectral density of the noise process $ x(n)$ . This is expressed by writing

$\displaystyle {\cal E}\{ \lim_{M\to\infty} P_{x,M}(\omega) \} = S_x(\omega)$ (7.24)

where $ S_x(\omega)$ denotes the power spectral density (PSD) of $ x$ . (``Expected value'' is defined in Appendix C on page [*].)

In terms of the sample PSD defined in §6.7, we have

$\displaystyle P_{x,M}(\omega) = M \hbox{asinc}_M^2 \ast {\hat S}_{x,M}(\omega).$ (7.25)

That is, the periodogram is equal to the smoothed sample PSD. In the time domain, the autocorrelation function corresponding to the periodogram is Bartlett windowed.

In practice, we of course compute a sampled periodogram $ S_x(\omega_k)$ , $ \omega_k = 2\pi/N$ , replacing the DTFT with the length $ N\ge M$ FFT. Essentially, the steps of §6.9 include computation of the periodogram.

As mentioned in §6.9, a problem with the periodogram of noise signals is that it too is random for most purposes. That is, while the noise has been split into bands by the Fourier transform, it has not been averaged in any way that reduces randomness, and each band produces a nearly independent random value. In fact, it can be shown [120] that $ P_{x,M}(\omega)$ is a random variable whose standard deviation (square root of its variance) is comparable to its mean.

In principle, we should be able to recover from $ P_{x,M}(\omega)$ a filter $ H_x(\omega)$ which, when used to filter white noise, creates a noise indistinguishable statistically from the observed sequence $ x(n)$ . However, the DTFT is evidently useless for this purpose. How do we proceed?

The trick to noise spectrum analysis is that many sample power spectra (squared-magnitude FFTs) must be averaged to obtain a ``stable'' statistical estimate of the noise spectral envelope. This is the essence of Welch's method for spectrum analysis of stochastic processes, as elaborated in §6.12 below. The right column of Fig.6.1 illustrates the effect of this averaging for white noise.

Matlab for the Periodogram

Octave and the Matlab Signal Processing Toolbox have a periodogram function. Matlab for computing a periodogram of white noise is given below (see top-right plot in Fig.6.1):

M = 32;
v = randn(M,1);       % white noise
V = abs(fft(v)).^2/M; % periodogram

Next Section:
Welch's Method
Previous Section:
Why an Impulse is Not White Noise