DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Choice of Lossless Feedback Matrix

As mentioned in §3.4, an ``ideal'' late reverberation impulse response should resemble exponentially decaying noise [314]. It is therefore useful when designing a reverberator to start with an infinite reverberation time (the ``lossless case'') and work on making the reverberator a good ``noise generator''. Such a starting point is ofen referred to as a lossless prototype [153,430]. Once smooth noise is heard in the impulse response of the lossless prototype, one can then work on obtaining the desired reverberation time in each frequency band (as will be discussed in §3.7.4 below).

In reverberators based on feedback delay networks (FDNs), the smoothness of the ``perceptually white noise'' generated by the impulse response of the lossless prototype is strongly affected by the choice of FDN feedback matrix as well as the (ideally mutually prime) delay-line lengths in the FDN (discussed further in §3.7.3 below). Following are some of the better known feedback-matrix choices.

Hadamard Matrix

A second-order Hadamard matrix may be defined by

$\displaystyle \mathbf{H}_2 \isdef \frac{1}{\sqrt{2}} \left[\begin{array}{rr} 1 & 1\\ -1 & 1 \end{array}\right], $

with higher order Hadamard matrices defined by recursive embedding, e.g.,

$\displaystyle \mathbf{H}_4 \isdef \frac{1}{\sqrt{2}} \left[\begin{array}{rr} \... ...}{rrrr} 1& 1& 1&1\\ -1& 1&-1&1\\ -1&-1& 1&1\\ 1&-1&-1&1 \end{array}\right]. $

When $ n$ is a power of $ 4$, the Hadamard matrix $ \mathbf{H}_n$ of that order requires no multiplies in fixed-point arithmetic. An $ n\times n$ Hadamard matrix has the maximum possible determinant of any $ n\times n$ complex matrix containing elements which are bounded by $ 1$ in magnitude. This can be seen as an optimal mixing and scattering property of the matrix.

As of version 0.9.30, Faust's math.lib4.12contains a function called hadamard(n) for generating an $ n\times n$ Hadamard matrix, where $ n$ must be a power of $ 2$. A Hadamard feedback matrix is used in the programming example reverb_designer.dsp (a configurable FDN reverberator) distributed with Faust.

A Hadamard feedback matrix is said to be used in the IRCAM Spatialisateur [218].

Householder Feedback Matrix

One choice of lossless feedback matrix $ \mathbf{A}_N$ for FDNs, especially nice in the $ 4\times4$ case, is a specific Householder reflection proposed by Jot [217]:

$\displaystyle \mathbf{A}_N = \mathbf{I}_N - \frac{2}{N}\uv_N\uv_N^T \protect$ (4.4)

where $ \uv_N^T = [1, 1, \dots, 1]$ can be interpreted as the specific vector about which the input vector is reflected in $ N$-dimensional space (followed by a sign inversion). More generally, the identity matrix $ \mathbf{I}_N$ can be replaced by any $ N\times N$ permutation matrix [153, p. 126].

It is interesting to note that when $ N$ is a power of 2, no multiplies are required [430]. For other $ N$, only one multiply is required (by $ 2/N$).

Another interesting property of the Householder reflection $ \mathbf{A}_N$ given by Eq.$ \,$(3.4) (and its permuted forms) is that an $ N\times N$ matrix-times-vector operation may be carried out with only $ 2N-1$ additions (by first forming $ \uv_N^T$ times the input vector, applying the scale factor $ 2/N$, and subtracting the result from the input vector). This is the same computation as physical wave scattering at a junction of identical waveguides (§C.8).

An example implementation of a Householder FDN for $ N=3$ is shown in Fig.3.11. As observed by Jot [153, p. 216], this computation is equivalent to $ N$ parallel feedback comb filters with one new feedback path from the output to the input through a gain of $ -2/N$.

Figure 3.11: FDN using a Householder-reflection feedback matrix.
\includegraphics[width=0.7\twidth]{eps/householder1}

A nice feature of the Householder feedback matrix $ A_N$ is that for $ N\neq 2$, all entries in the matrix are nonzero. This means every delay line feeds back to every other delay line, thereby helping to maximize echo density as soon as possible.

Furthermore, for $ N=4$, all matrix entries have the same magnitude:

$\displaystyle \mathbf{A}_4 = \frac{1}{2} \left[\begin{array}{rrrr} 1 & -1 & -1 ... ... -1 & 1 & -1 & -1\\ -1 & -1 & 1 & -1\\ -1 & -1 & -1 & 1 \end{array}\right]. $

Only the $ N=4$ case is ``balanced'' in this way. For larger $ N$, the diagonal becomes larger than the off-diagonal elements, and as $ N$ becomes very large, the FDN approaches a bank of decoupled parallel comb filters.

Due to the elegant balance of the $ N=4$ Householder feedback matrix, Jot [216] proposes an $ N=16$ FDN based on an embedding of $ N=4$ feedback matrices:

$\displaystyle \mathbf{A}_{16} = \frac{1}{2} \left[\begin{array}{rrrr} \mathbf{A... ...\mathbf{A}_4 & -\mathbf{A}_4 & -\mathbf{A}_4 & \mathbf{A}_4 \end{array}\right] $

Another method is to replace each of the four delay lines in an FDN(4) by a Gerzon vector allpass (see §2.8.5) which is $ 4\times4$ and contains four delay lines.

Householder Reflections

For completeness, this section derives the Householder reflection matrix from geometric considerations [451]. Let $ \mathbf{P}_{\underline{u}}$ denote the projection matrix which orthogonally projects vectors onto $ {\underline{u}}$, i.e.,

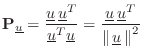
$\displaystyle \mathbf{P}_{\underline{u}}= \frac{\underline{u}\,\underline{u}^T}... ...frac{\underline{u}\,\underline{u}^T}{\left\Vert\,\underline{u}\,\right\Vert^2} $

and

$\displaystyle \mathbf{P}_{\underline{u}}\, \underline{x}= \underline{u}\,\frac{... ...<\underline{u},\underline{x}\right>}{\left\Vert\,\underline{u}\,\right\Vert^2} $

specifically projects $ \underline{x}$ onto $ \underline{u}$. Since the projection is orthogonal, we have

$\displaystyle \left<\underline{x}-\mathbf{P}_{\underline{u}}\underline{x},\unde... ...}-\mathbf{P}_{\underline{u}})\underline{x},\underline{u}\right>=\underline{0}. $

We may interpret $ (\mathbf{I}-\mathbf{P}_{\underline{u}})\underline{x}$ as the difference vector between $ \underline{x}$ and $ \mathbf{P}_{\underline{u}}\underline{x}$, its orthogonal projection onto $ \underline{u}$, since

$\displaystyle (\mathbf{I}-\mathbf{P}_{\underline{u}})\underline{x}+ \mathbf{P}_{\underline{u}}\underline{x}= \underline{x} $

and we have $ (\mathbf{I}-\mathbf{P}_{\underline{u}})\underline{x}\perp \mathbf{P}_{\underline{u}}\underline{x}$ by definition of the orthogonal projection. Consequently, the projection onto $ \underline{u}$ minus this difference vector gives a reflection of the vector $ \underline{x}$ about $ \underline{u}$:

$\displaystyle \underline{y}= \mathbf{P}_{\underline{u}}\underline{x}- (\mathbf{... ...line{u}})\underline{x}= (2\mathbf{P}_{\underline{u}}- \mathbf{I})\underline{x} $

Thus, $ \underline{y}$ is obtained by reflecting $ \underline{x}$ about $ \underline{u}$--a so-called Householder reflection.

Most General Lossless Feedback Matrices

As shown in §C.15.3, an FDN feedback matrix $ \mathbf{A}_N$ is lossless if and only if its eigenvalues have modulus 1 and its $ N$ eigenvectors are linearly independent.

A unitary matrix $ Q$ is any (complex) matrix that is inverted by its own (conjugate) transpose:

$\displaystyle Q^{-1} = Q^H, $

where $ Q^H$ denotes the Hermitian conjugate (i.e., the complex-conjugate transpose) of $ Q$. When $ Q$ is real (as opposed to complex), we may simply call it an orthogonal matrix, and we write $ Q^{-1} = Q^T$, where $ T$ denotes matrix transposition.

All unitary (and orthogonal) matrices have unit-modulus eigenvalues and linearly independent eigenvectors. As a result, when used as a feedback matrix in an FDN, the resulting FDN will be lossless (until the delay-line damping filters are inserted, as discussed in §3.7.4 below).

Triangular Feedback Matrices

An interesting class of feedback matrices, also explored by Jot [216], is that of triangular matrices. A basic fact from linear algebra is that triangular matrices (either lower or upper triangular) have all of their eigenvalues along the diagonal.4.13 For example, the matrix

$\displaystyle \mathbf{A}_3 = \left[\begin{array}{ccc} \lambda_1 & 0 & 0\\ [2pt] a & \lambda_2 & 0\\ [2pt] b & c & \lambda_3 \end{array}\right] $

is lower triangular, and its eigenvalues are $ (\lambda_1, \lambda_2,\lambda_3)$ for all values of $ a$, $ b$, and $ c$.

It is important to note that not all triangular matrices are lossless. For example, consider

$\displaystyle \mathbf{A}_2 = \left[\begin{array}{cc} 1 & 0 \\ [2pt] 1 & 1 \end{array}\right] $

It has two eigenvalues equal to 1, which looks lossless, but a quick calculation shows that there is only one eigenvector, $ [0,1]^T$. This happens because this matrix is a Jordan block of order 2 corresponding to the repeated eigenvalue $ \lambda=1$. A direct computation shows that

$\displaystyle \mathbf{A}_2^n = \left[\begin{array}{cc} 1 & 0 \\ [2pt] n & 1 \end{array}\right] $

which is clearly not lossless.

One way to avoid ``coupled repeated poles'' of this nature is to use non-repeating eigenvalues. Another is to convert $ \mathbf{A}$ to Jordan canonical form by means of a similarity transformation, zero any off-diagonal elements, and transform back [329].

Next Section:
Choice of Delay Lengths
Previous Section:
History of FDNs for Artificial Reverberation