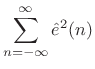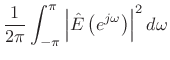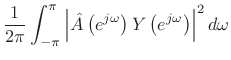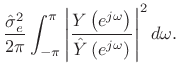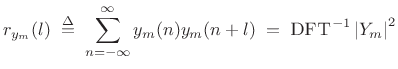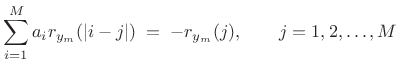DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Linear Prediction Spectral Envelope

Linear Prediction (LP) implicitly computes a spectral envelope that is well adapted for audio work, provided the order of the predictor is appropriately chosen. Due to the error minimized by LP, spectral peaks are emphasized in the envelope, as they are in the auditory system. (The peak-emphasis of LP is quantified in (10.10) below.)

The term ``linear prediction'' refers to the process of predicting a signal sample $ y(n)$ based on $ M$ past samples:

$\displaystyle y(n) \eqsp -a_1 y(n-1) - a_2 y(n-2) - \cdots - a_M y(n-M) + e(n) \protect$ (11.4)

We call $ M$ the order of the linear predictor, and $ \{a_i\}_{i=1}^M$ the prediction coefficients. The prediction error (or ``innovations sequence'' [114]) is denoted $ e(n)$ in (10.4), and it represents all new information entering the signal $ y$ at time $ n$ . Because the information is new, $ e(n)$ is ``unpredictable.'' The predictable component of $ y(n)$ contains no new information.

Taking the z transform of (10.4) yields

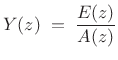$\displaystyle Y(z) \eqsp \frac{E(z)}{A(z)}$ (11.5)

where $ A(z) = 1 + a_1z^{-1}+ \cdots a_M z^{-M}$ . In signal modeling by linear prediction, we are given the signal $ y(n)$ but not the prediction coefficients $ a_i$ . We must therefore estimate them. Let $ {\hat A}(z) = 1 + {\hat a}_1z^{-1} + \cdots {\hat a}_M z^{-M}$ denote the polynomial with estimated prediction coefficients $ {\hat a}_i$ . Then we have

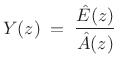$\displaystyle Y(z) \eqsp \frac{{\hat E}(z)}{{\hat A}(z)}$ (11.6)

where $ {\hat E}(z)$ denotes the estimated prediction-error z transform. By minimizing $ \vert\vert\,{\hat E}\,\vert\vert _2$ , we define a minimum-least-squares estimate $ {\hat A}$ . In other words, the linear prediction coefficients $ {\hat a}_i$ are defined as those which minimize the sum of squared prediction errors $ {\hat e}(n)$

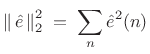$\displaystyle \left\Vert\,{\hat e}\,\right\Vert _2^2 \eqsp \sum_n {\hat e}^2(n)$ (11.7)

over some range of $ n$ , typically an interval over which the signal is stationary (defined in Chapter 6). It turns out that this minimization results in maximally flattening the prediction-error spectrum $ E(z)$ [11,157,162]. That is, the optimal $ {\hat A}(z)$ is a whitening filter (also called an inverse filter). This makes sense in terms of Chapter 6 when one considers that a flat power spectral density corresponds to white noise in the time domain, and only white noise is completely unpredictable from one sample to the next. A non-flat spectrum corresponds to a nonzero correlation between two signal samples separated by some nonzero time interval.

If the prediction-error is successfully whitened, then the signal model can be expressed in the frequency domain as

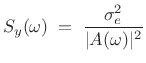$\displaystyle S_y(\omega) \eqsp \frac{\sigma^2_e}{\vert A(\omega)\vert^2}$ (11.8)

where $ S_y(\omega)$ denotes the power spectral density of $ y$ (defined in Chapter 6), and $ \sigma_e^2$ denotes the variance of the (white-noise) prediction error $ e(n)$ . Thus, the spectral magnitude envelope may be defined as

EnvelopeLPC$\displaystyle _y(\omega) \eqsp \frac{\sigma_e}{\vert A(\omega)\vert}$ (11.9)

Linear Prediction is Peak Sensitive

By Rayleigh's energy theorem, $ \vert\vert\,{\hat e}\,\vert\vert _2= \vert\vert\,{\hat E}\,\vert\vert _2$ (as shown in §2.3.8). Therefore,

$\displaystyle \sum_{n=-\infty}^{\infty} {\hat e}^2(n)$ $\displaystyle =$ $\displaystyle \frac{1}{2\pi}\int_{-\pi}^{\pi}\left\vert{\hat E}\left(e^{j\omega}\right)\right\vert^2 d\omega$  
  $\displaystyle \isdef$ $\displaystyle \frac{1}{2\pi}\int_{-\pi}^{\pi}\left\vert{\hat A}\left(e^{j\omega}\right)Y\left(e^{j\omega}\right)\right\vert^2 d\omega$  
  $\displaystyle =$ $\displaystyle \frac{{\hat\sigma}^2_e}{2\pi}\int_{-\pi}^{\pi}\left\vert\frac{Y\left(e^{j\omega}\right)}% {{\hat Y}\left(e^{j\omega}\right)}\right\vert^2 d\omega. \protect$ (11.10)

From this ``ratio error'' expression in the frequency domain, we can see that contributions to the error are smallest when $ \vert{\hat Y}(e^{j\omega})\vert>\vert Y(e^{j\omega})\vert$ . Therefore, LP tends to overestimate peaks. LP cannot make $ \vert{\hat Y}\vert$ arbitrarily large because $ A(z)$ is constrained to be monic and minimum-phase. It can be shown that the log-magnitude frequency response of every minimum-phase monic polynomial $ A(z)$ is zero-mean [162]. Therefore, for each peak overestimation, there must be an equal-area ``valley underestimation'' (in a log-magnitude plot over the unit circle).

Linear Prediction Methods

The two classic methods for linear prediction are called the autocorrelation method and the covariance method [162,157]. Both methods solve the linear normal equations (defined below) using different autocorrelation estimates.

In the autocorrelation method of linear prediction, the covariance matrix is constructed from the usual Bartlett-window-biased sample autocorrelation function (see Chapter 6), and it has the desirable property that $ {\hat A}(z)$ is always minimum phase (i.e., $ 1/{\hat A}(z)$ is guaranteed to be stable). However, the autocorrelation method tends to overestimate formant bandwidths; in other words, the filter model is typically overdamped. This can be attributed to implicitly ``predicting zero'' outside of the signal frame, resulting in the Bartlett-window bias in the sample autocorrelation.

The covariance method of LP is based on an unbiased autocorrelation estimate (see Eq.$ \,$ (6.4)). As a result, it gives more accurate bandwidths, but it does not guarantee stability.

So-called covariance lattice methods and Burg's method were developed to maintain guaranteed stability while giving accuracy comparable to the covariance method of LP [157].

Computation of Linear Prediction Coefficients

In the autocorrelation method of linear prediction, the linear prediction coefficients $ \{a_i\}_{i=1}^M$ are computed from the Bartlett-window-biased autocorrelation function (Chapter 6):

$\displaystyle r_{y_m}(l) \isdefs \sum_{n=-\infty}^\infty y_m(n)y_m(n+l) \eqsp \hbox{\sc DFT}^{-1}\left\vert Y_m\right\vert^2 \protect$ (11.11)

where $ y_m$ denotes the $ m$ th data frame from the signal $ y$ . To obtain the $ M$ th-order linear predictor coefficients $ \{a_1,\ldots,a_M\}$ , we solve the following $ M\times M$ system of linear normal equations (also called Yule-Walker or Wiener-Hopf equations):

$\displaystyle \sum_{i=1}^M a_i r_{y_m}(\vert i-j\vert) \eqsp -r_{y_m}(j), \qquad j=1,2,\ldots,M \protect$ (11.12)

In matlab syntax, the solution is given by `` $ \verb+a=R\p+$ '', where $ \verb+p(j)+ = r_{y_m}(j)$ , and $ \verb+R(i,j)+=r_{y_m}(\vert i-j\vert)$ . Since the covariance matrix $ R$ is symmetric and Toeplitz by construction,11.4 an $ O(M^2)$ solution exists using the Durbin recursion.11.5

If the rank of the $ M\times M$ autocorrelation matrix $ R[i,j]=r_{y_n}(\vert i-j\vert)$ is $ M$ , then the solution to (10.12) is unique, and this solution is always minimum phase [162] (i.e., all roots of $ A(z)$ are inside the unit circle in the $ z$ plane [263], so that $ 1/A(z)$ is always a stable all-pole filter). In practice, the rank of $ R$ is $ M$ (with probability 1) whenever $ y(n)$ includes a noise component. In the noiseless case, if $ y(n)$ is a sum of sinusoids, each (real) sinusoid at distinct frequency $ 0<\omega_i T < \pi$ adds 2 to the rank. A dc component, or a component at half the sampling rate, adds 1 to the rank of $ R$ .

The choice of time window for forming a short-time sample autocorrelation and its weighting also affect the rank of $ R$ . Equation (10.11) applied to a finite-duration frame yields what is called the autocorrelation method of linear prediction [162]. Dividing out the Bartlett-window bias in such a sample autocorrelation yields a result closer to the covariance method of LP. A matlab example is given in §10.3.3 below.

The classic covariance method computes an unbiased sample covariance matrix by limiting the summation in (10.11) to a range over which $ y_m(n+l)$ stays within the frame--a so-called ``unwindowed'' method. The autocorrelation method sums over the whole frame and replaces $ y_m(n+l)$ by zero when $ n+l$ points outside the frame--a so-called ``windowed'' method (windowed by the rectangular window).

Linear Prediction Order Selection

For computing spectral envelopes via linear prediction, the order $ M$ of the predictor should be chosen large enough that the envelope can follow the contour of the spectrum, but not so large that it follows the spectral ``fine structure'' on a scale not considered to belong in the envelope. In particular, for voice, $ M$ should be twice the number of spectral formants, and perhaps a little larger to allow more detailed modeling of spectral shape away from the formants. For a sum of quasi sinusoids, the order $ M$ should be significantly less than twice the number of sinusoids to inhibit modeling the sinusoids as spectral-envelope peaks. For filtered-white-noise, $ M$ should be close to the order of the filter applied to the white noise, and so on.

Summary of LP Spectral Envelopes

In summary, the spectral envelope of the $ m$ th spectral frame, computed by linear prediction, is given by

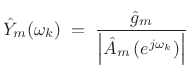$\displaystyle {\hat Y}_m(\omega_k) \eqsp \frac{{\hat g}_m}{\left\vert{\hat A}_m\left(e^{j\omega_k }\right)\right\vert}$ (11.13)

where $ {\hat A}_m$ is computed from the solution of the Toeplitz normal equations, and $ {\hat g}_m = \vert\vert\,{\hat E}_m\,\vert\vert _2$ is the estimated rms level of the prediction error in the $ m$ th frame.

The stable, all-pole filter

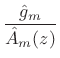$\displaystyle \frac{{\hat g}_m}{{\hat A}_m(z)}$ (11.14)

can be driven by unit-variance white noise to produce a filtered-white-noise signal having spectral envelope $ {\hat g}_m/\vert{\hat A}_m(e^{j\omega_k })\vert$ . We may regard $ {\hat g}_m/{\hat A}_m(e^{j\omega_k })$ (no absolute value) as the frequency response of the filter in a source-filter decomposition of the signal $ y_m(n)$ , where the source is white noise.

It bears repeating that $ \log A(e^{j\omega_k })$ is zero mean when $ A(z)$ is monic and minimum phase (all zeros inside the unit circle). This means, for example, that $ \log {\hat g}_m$ can be simply estimated as the mean of the log spectral magnitude $ \log \vert Y_m(e^{j\omega_k })\vert$ .

For best results, the frequency axis ``seen'' by linear prediction should be warped to an auditory frequency scale, as discussed in Appendix E [123]. This has the effect of increasing the accuracy of low-frequency peaks in the extracted spectral envelope, in accordance with the nonuniform frequency resolution of the inner ear.

Next Section:
Spectral Envelope Examples
Previous Section:
Cepstral Windowing