Summary
Our historical tour touched upon the following milestones in audio spectral modeling, among others:
- Bernoulli's understanding of superimposed sinusoidal vibrations (1733)
- Fourier's theorem (1822)
- Helmholtz's understanding of the ear as a spectrum analyzer (1863)
- Telharmonium (1898)
- Hammond Organ (1934)
- Vocoder (1935)
- Voder (1937)
- Phase Vocoder (1966)
- Additive Synthesis in computer music (1969)
- FM Brass Synthesis (1970)
- Synclavier 8-bit FM/Additive synthesizer (1975)
- FM singing voice (1978)
- Yamaha DX-7 (1983)
- Sinusoidal Modeling (1977,1979,1985)
- Sines + Noise (1988)
- Sines + Noise + Transients (1988,1996,1998,2000)
Choice of Hop Size
A question related to the STFT analysis window is the hop size ![]() ,
i.e., how much we can advance the analysis time origin from frame to
frame. This depends very much on the purposes of the analysis. In
general, more overlap will give more analysis points and therefore
smoother results across time, but the computational expense is
proportionately greater. For purposes of spectrogram display or
additive synthesis parameter extraction, a conservative constraint
is to require that the analysis window overlap-add to a constant
at the chosen hop size:
,
i.e., how much we can advance the analysis time origin from frame to
frame. This depends very much on the purposes of the analysis. In
general, more overlap will give more analysis points and therefore
smoother results across time, but the computational expense is
proportionately greater. For purposes of spectrogram display or
additive synthesis parameter extraction, a conservative constraint
is to require that the analysis window overlap-add to a constant
at the chosen hop size:
where
The COLA constraint can be overly conservative for steady-state signals. For additive synthesis purposes, it is more efficient and still effective to increase the hop size to the number of samples over which the spectrum is not changing appreciably. In the case of the steady-state portion of piano tones, the hop size appears to be limited by the fastest amplitude envelope ``beat'' frequency caused by mistuning strings on one key or by overlapping partials from different keys.
For certain window types (such as sum-of-cosine windows, as discussed
in Chapter 3), there exist perfect overlap factors in the sense
of (H.1). For example, a rectangular window can hop by ![]() ,
where
,
where ![]() is any positive integer, and a Hanning or Hamming window can
use any hop size of the form
is any positive integer, and a Hanning or Hamming window can
use any hop size of the form ![]() . For the Kaiser window, in
contrast, there is no perfect hop size other than
. For the Kaiser window, in
contrast, there is no perfect hop size other than ![]() .
.
The COLA criterion for windows and their hop sizes is not the best
perspective to take when overlap-add synthesis is being constructed
from the modified spectra
![]() [7]. As discussed in Chapter 9, the hop size
[7]. As discussed in Chapter 9, the hop size ![]() is the
decimation factor applied to each FFT filter-bank output, and the
window is the envelope of each filter's impulse response. The
decimation by
is the
decimation factor applied to each FFT filter-bank output, and the
window is the envelope of each filter's impulse response. The
decimation by ![]() causes aliasing, and the frame rate
causes aliasing, and the frame rate ![]() is equal to twice the ``folding frequency'' of this aliasing.
Consequently, to minimize aliasing, the choice of hop size
is equal to twice the ``folding frequency'' of this aliasing.
Consequently, to minimize aliasing, the choice of hop size ![]() should
be such that the folding frequency exceeds the ``cut-off frequency'' of
the window. The cut-off frequency of a window can be defined as the
frequency above which the window transform magnitude is less than or
equal to the worst-case side-lobe level. For convenience, we typically
use the frequency of the first zero-crossing beyond the main lobe as
the definition of cut-off frequency. Following this rule yields
should
be such that the folding frequency exceeds the ``cut-off frequency'' of
the window. The cut-off frequency of a window can be defined as the
frequency above which the window transform magnitude is less than or
equal to the worst-case side-lobe level. For convenience, we typically
use the frequency of the first zero-crossing beyond the main lobe as
the definition of cut-off frequency. Following this rule yields ![]() overlap for the rectangular window,
overlap for the rectangular window, ![]() overlap for Hamming and
Hanning windows, and
overlap for Hamming and
Hanning windows, and ![]() (5/6) overlap for Blackman windows. The
hop size usable with a Kaiser window is determined by its design
parameters (principally, the desired time-bandwidth product of the
window, or, the ``beta'' parameter) [115].
(5/6) overlap for Blackman windows. The
hop size usable with a Kaiser window is determined by its design
parameters (principally, the desired time-bandwidth product of the
window, or, the ``beta'' parameter) [115].
One may wonder what happens to aliasing in the perfect-reconstruction case in which (H.1) is satisfied. The answer is that aliasing does occur in the individual filter-bank outputs, but this aliasing is canceled in the reconstruction by overlap-add if there were no modifications to the STFT. For a general discussion of aliasing cancellation in decimated filter banks, see Chapter 11 (especially §11.4.5) and/or [287].
Filling the FFT Input Buffer (Step 2)
The FFT size ![]() is normally chosen to be the first power of two that
is at least twice the window length
is normally chosen to be the first power of two that
is at least twice the window length ![]() , with the difference
, with the difference ![]() filled with zeros (``zero-padded''). The reason for increasing the FFT
size and filling in with zeros is that zero-padding in the time domain
corresponds to interpolation in the frequency domain, and
interpolating the spectrum is useful in various ways. First, the
problem of finding spectral peaks which are not exact bin frequencies
is made easier when the spectrum is more densely sampled. Second,
plots of the magnitude of the more smoothly sampled spectrum are less
likely to confuse the untrained eye. (Only signals truly periodic in
filled with zeros (``zero-padded''). The reason for increasing the FFT
size and filling in with zeros is that zero-padding in the time domain
corresponds to interpolation in the frequency domain, and
interpolating the spectrum is useful in various ways. First, the
problem of finding spectral peaks which are not exact bin frequencies
is made easier when the spectrum is more densely sampled. Second,
plots of the magnitude of the more smoothly sampled spectrum are less
likely to confuse the untrained eye. (Only signals truly periodic in
![]() samples should not be zero-padded. They should also be windowed
only by the Rectangular window.) Third, for overlap-add synthesis from
spectral modifications, the zero-padding allows for multiplicative
modification in the frequency domain (convolutional modification in
the time domain) without time aliasing in the inverse FFT. The length
of the allowed convolution in the time domain (the impulse response of
the effective digital filter) equals the number of extra zeros (plus
one) in the zero padding.
samples should not be zero-padded. They should also be windowed
only by the Rectangular window.) Third, for overlap-add synthesis from
spectral modifications, the zero-padding allows for multiplicative
modification in the frequency domain (convolutional modification in
the time domain) without time aliasing in the inverse FFT. The length
of the allowed convolution in the time domain (the impulse response of
the effective digital filter) equals the number of extra zeros (plus
one) in the zero padding.
If ![]() is the number of samples in the main lobe when the
zero-padding factor is 1 (
is the number of samples in the main lobe when the
zero-padding factor is 1 (![]() ), then a zero-padding factor of
), then a zero-padding factor of ![]() gives
gives ![]() samples for the same main lobe (and same main-lobe
bandwidth). The zero-padding (interpolation) factor
samples for the same main lobe (and same main-lobe
bandwidth). The zero-padding (interpolation) factor ![]() should
be large enough to enable accurate estimation of the true maximum of
the main lobe after it has been frequency shifted by some arbitrary
amount equal to the frequency of a sinusoidal component in the input
signal. We have determined by computational search that, for a
rectangularly windowed sinusoid (of any frequency), quadratic
frequency interpolation (using the three highest bins) yields at
least
should
be large enough to enable accurate estimation of the true maximum of
the main lobe after it has been frequency shifted by some arbitrary
amount equal to the frequency of a sinusoidal component in the input
signal. We have determined by computational search that, for a
rectangularly windowed sinusoid (of any frequency), quadratic
frequency interpolation (using the three highest bins) yields at
least ![]() (of the distance from the sinc peak to the first
zero-crossing) accuracy if the zero-padding factor
(of the distance from the sinc peak to the first
zero-crossing) accuracy if the zero-padding factor ![]() is 5 or
higher.
is 5 or
higher.
![\includegraphics[width=\twidth,height=0.9\textheight]{eps/fig3}](http://www.dsprelated.com/josimages_new/sasp2/img3045.png) |
As mentioned in the previous section, we facilitate phase detection
by using a zero-phase window, i.e., the windowed data (using an odd
length window) is centered about the time origin. A zero-centered,
length ![]() data frame appears in the length
data frame appears in the length ![]() FFT input buffer as
shown in Fig.H.1c. The first
FFT input buffer as
shown in Fig.H.1c. The first ![]() samples of the windowed
data, the ``negative-time'' portion, will be stored at the end of the
buffer, from sample
samples of the windowed
data, the ``negative-time'' portion, will be stored at the end of the
buffer, from sample ![]() to
to ![]() , and the remaining
, and the remaining ![]() samples, the zero- and ``positive-time'' portion, will be stored
starting at the beginning of the buffer, from sample 0
to
samples, the zero- and ``positive-time'' portion, will be stored
starting at the beginning of the buffer, from sample 0
to
![]() . Thus, all zero padding occurs in the middle of the
FFT input buffer.
. Thus, all zero padding occurs in the middle of the
FFT input buffer.
Peak Detection (Steps 3 and 4)
Due to the sampled nature of spectra obtained using the STFT, each
peak (location and height) found by finding the maximum-magnitude
frequency bin is only accurate to within half a bin. A bin represents
a frequency interval of ![]() Hz, where
Hz, where ![]() is the FFT size.
Zero-padding increases the number of FFT bins per Hz and thus
increases the accuracy of the simple peak detection. However, to
obtain frequency accuracy on the level of
is the FFT size.
Zero-padding increases the number of FFT bins per Hz and thus
increases the accuracy of the simple peak detection. However, to
obtain frequency accuracy on the level of ![]() of the distance
from a sinc maximum to its first zero crossing (in the case of a
rectangular window), the zero-padding factor required is
of the distance
from a sinc maximum to its first zero crossing (in the case of a
rectangular window), the zero-padding factor required is ![]() .
(Note that with no zero padding, the STFT analysis parameters are
typically arranged so that the distance from the sinc peak to its
first zero-crossing is equal to the fundamental frequency of a
harmonic sound. Under these conditions,
.
(Note that with no zero padding, the STFT analysis parameters are
typically arranged so that the distance from the sinc peak to its
first zero-crossing is equal to the fundamental frequency of a
harmonic sound. Under these conditions, ![]() of this interval is
equal to the relative accuracy in the fundamental frequency
measurement. Thus, this is a realistic specification in view of pitch
discrimination accuracy.) Since we would nominally take two periods
into the data frame (for a Rectangular window), a
of this interval is
equal to the relative accuracy in the fundamental frequency
measurement. Thus, this is a realistic specification in view of pitch
discrimination accuracy.) Since we would nominally take two periods
into the data frame (for a Rectangular window), a ![]() Hz sinusoid
at a sampling rate of
Hz sinusoid
at a sampling rate of ![]() KHz would have a period of
KHz would have a period of
![]() samples, so that the FFT size would have to exceed
one million. A more efficient spectral interpolation scheme is to
zero-pad only enough so that quadratic (or other simple) spectral
interpolation, using only bins immediately surrounding the
maximum-magnitude bin, suffices to refine the estimate to
samples, so that the FFT size would have to exceed
one million. A more efficient spectral interpolation scheme is to
zero-pad only enough so that quadratic (or other simple) spectral
interpolation, using only bins immediately surrounding the
maximum-magnitude bin, suffices to refine the estimate to ![]() accuracy. PARSHL uses a parabolic interpolator which fits a parabola
through the highest three samples of a peak to estimate the true peak
location and height (cf. Fig.H.2).
accuracy. PARSHL uses a parabolic interpolator which fits a parabola
through the highest three samples of a peak to estimate the true peak
location and height (cf. Fig.H.2).
We have seen that each sinusoid appears as a shifted window transform which is a sinc-like function. A robust method for estimating peak frequency with very high accuracy would be to fit a window transform to the sampled spectral peaks by cross-correlating the whole window transform with the entire spectrum and taking and interpolated peak location in the cross-correlation function as the frequency estimate. This method offers much greater immunity to noise and interference from other signal components.
To describe the parabolic interpolation strategy, let's define a
coordinate system centered at
![]() , where
, where ![]() is the bin
number of the spectral magnitude maximum, i.e.,
is the bin
number of the spectral magnitude maximum, i.e.,
![]() for all
for all
![]() . An example is shown in
Figure 4. We desire a general parabola of the form
. An example is shown in
Figure 4. We desire a general parabola of the form
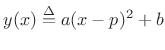 |
(H.2) |
such that
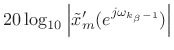 |
(H.3) | ||
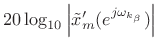 |
(H.4) | ||
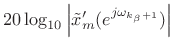 |
(H.5) |
We have found empirically that the frequencies tend to be about twice as accurate when dB magnitude is used rather than just linear magnitude. An interesting open question is what is the optimum nonlinear compression of the magnitude spectrum when quadratically interpolating it to estimate peak locations.
Solving for the parabola peak location ![]() , we get
, we get
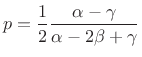 |
(H.6) |
and the estimate of the true peak location (in bins) will be
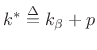 |
(H.7) |
and the peak frequency in Hz is
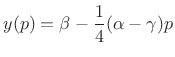 |
(H.8) |
The magnitude spectrum is used to find
Once an interpolated peak location has been found, the entire local maximum in the spectrum is removed. This allows the same algorithm to be used for the next peak. This peak detection and deletion process is continued until the maximum number of peaks specified by the user is found.
Peak Matching (Step 5)
The peak detection process returns the prominent peaks in a given frame sorted by frequency. The next step is to assign some subset of these peaks to oscillator trajectories, which is done by the peak matching algorithm. If the number of spectral peaks were constant with slowly changing amplitudes and frequencies along the sound, this task would be straightforward. However, it is not always immediately obvious how to connect the spectral peaks of one frame with those of the next.
To describe the peak matching process, let's assume that the frequency
tracks were initialized at frame ![]() and we are currently at frame
and we are currently at frame
![]() . Suppose that at frame
. Suppose that at frame ![]() the frequency values for the
the frequency values for the ![]() tracks are
tracks are
![]() , and that we want to match them
to the
, and that we want to match them
to the ![]() peaks, with frequencies
peaks, with frequencies
![]() , of frame
, of frame
![]() .
.
Each track looks for its peak in frame ![]() by finding the one which
is closest in frequency to its current value. The
by finding the one which
is closest in frequency to its current value. The ![]() th track claims
frequency
th track claims
frequency ![]() for which
for which
![]() is minimum. The change in
frequency must be less than a specified maximum
is minimum. The change in
frequency must be less than a specified maximum
![]() , which
can be a frequency-dependent limit (e.g., linear, corresponding to a
relative frequency change limit). The possible situations are as follows:
, which
can be a frequency-dependent limit (e.g., linear, corresponding to a
relative frequency change limit). The possible situations are as follows:
12pt (1) If a match is found inside the maximum change limit, the track is continued (unless there is a conflict to resolve, as described below).
12pt
(2) If no match is made, it is assumed that the track with frequency
![]() must ``turn off'' entering frame
must ``turn off'' entering frame ![]() , and
, and ![]() is matched
to itself with zero magnitude. Since oscillator amplitudes are
linearly ramped from one the frame to the next, the terminating
track will ramp to zero over the duration of one frame hop.
This track will still exist (at zero amplitude), and if it
ever finds a frame with a spectral peak within its capture range
is matched
to itself with zero magnitude. Since oscillator amplitudes are
linearly ramped from one the frame to the next, the terminating
track will ramp to zero over the duration of one frame hop.
This track will still exist (at zero amplitude), and if it
ever finds a frame with a spectral peak within its capture range
![]() , it will ``turned back on,'' ramping its amplitude
up to the newly detected value. It is sometimes necessary to introduce
some hysteresis into the turning on and off process in order to prevent
``burbling'' of the tracks whose peaks sometimes make the cut and
sometimes don't. Normally this problem can be avoided by searching
for many more spectral peaks than there are oscillators to allocate.
, it will ``turned back on,'' ramping its amplitude
up to the newly detected value. It is sometimes necessary to introduce
some hysteresis into the turning on and off process in order to prevent
``burbling'' of the tracks whose peaks sometimes make the cut and
sometimes don't. Normally this problem can be avoided by searching
for many more spectral peaks than there are oscillators to allocate.
12pt (3) If a track finds a match which has already been claimed by another track, we give the peak to the track which is closest in frequency, and the ``losing'' track looks for another match. If the current track loses the conflict, it simply picks the best available non-conflicting peak. If the current track wins the conflict, it calls the assignment procedure recursively on behalf of the dislodged track. When the dislodged track finds the same peak and wants to claim it, it will see there is a conflict which it loses and will move on. This process is repeated for each track, solving conflicts recursively, until all existing tracks are matched or ``turned-off''.
After each track has extended itself forward in time or turned off,
the peaks of frame ![]() which have not been used are considered to be
new trajectories and a new track is ``started-up'' for each one of
them up to the maximum number of oscillators specified (which again
should be less than the number of spectral peaks detected). The new
oscillator tracks are started at frame
which have not been used are considered to be
new trajectories and a new track is ``started-up'' for each one of
them up to the maximum number of oscillators specified (which again
should be less than the number of spectral peaks detected). The new
oscillator tracks are started at frame ![]() with zero magnitude and
ramp to the correct amplitude at the current frame
with zero magnitude and
ramp to the correct amplitude at the current frame ![]() .
.
Once the program has finished, the peak trajectories for a sound look as in Fig.H.4.
Parameter Modifications (Step 6)
The possibilities that STFT techniques offer for modifying the analysis results before resynthesis have an enormous number of musical applications. Quatieri and McAulay [222] give a good discussion of some useful modifications for speech applications. By scaling and/or resampling the amplitude and the frequency trajectories, a host of sound transformations can be accomplished.
Time-scale modifications can be accomplished by resampling the
amplitude, frequency, and phase trajectories. This can be done
simply by changing the hop size ![]() in the resynthesis (although for
best results the hop size should change adaptively, avoiding
time-scale modifications during voice consonants or attacks, for
example). This has the effect of slowing down or speeding up the
sound while maintaining pitch and formant structure. Obviously this
can also be done for a time-varying modification by having a
time-varying hop size
in the resynthesis (although for
best results the hop size should change adaptively, avoiding
time-scale modifications during voice consonants or attacks, for
example). This has the effect of slowing down or speeding up the
sound while maintaining pitch and formant structure. Obviously this
can also be done for a time-varying modification by having a
time-varying hop size ![]() . However, due to the sinusoidal
representation, when a considerable time stretch is done in a
``noisy'' part of a sound, the individual sinewaves start to be heard
and the noise-like quality is lost.
. However, due to the sinusoidal
representation, when a considerable time stretch is done in a
``noisy'' part of a sound, the individual sinewaves start to be heard
and the noise-like quality is lost.
Frequency transformations, with or without time scaling, are also possible. A simple one is to scale the frequencies to alter pitch and formant structure together. A more powerful class of spectral modifications comes about by decoupling the sinusoidal frequencies (which convey pitch and inharmonicity information) from the spectral envelope (which conveys formant structure so important to speech perception and timbre). By measuring the formant envelope of a harmonic spectrum (e.g., by drawing straight lines or splines across the tops of the sinusoidal peaks in the spectrum and then smoothing), modifications can be introduced which only alter the pitch or only alter the formants. Other ways to measure formant envelopes include cepstral smoothing [198] and the fitting of low-order LPC models to the inverse FFT of the squared magnitude of the spectrum [157]. By modulating the flattened (by dividing out the formant envelope) spectrum of one sound by the formant-envelope of a second sound, ``cross-synthesis'' is obtained. Much more complex modifications are possible.
Not all spectral modifications are ``legal,'' however. As mentioned earlier, multiplicative modifications (simple filtering, equalization, etc.) are straightforward; we simply zero-pad sufficiently to accommodate spreading in time due to convolution. It is also possible to approximate nonlinear functions of the spectrum in terms of polynomial expansions (which are purely multiplicative). When using data derived filters, such as measured formant envelopes, it is a good idea to smooth the spectral envelopes sufficiently that their inverse FFT is shorter in duration than the amount of zero-padding provided. One way to monitor time-aliasing distortion is to measure the signal energy at the midpoint of the inverse-FFT output buffer, relative to the total energy in the buffer, just before adding it to the final outgoing overlap-add reconstruction; little relative energy in the ``maximum-positive'' and ``minimum negative'' time regions indicates little time aliasing. The general problem to avoid here is drastic spectral modifications which correspond to long filters in the time domain for which insufficient zero-padding has been provided. An inverse FFT of the spectral modification function will show its time duration and indicate zero-padding requirements. The general rule (worth remembering in any audio filtering context) is ``be gentle in the frequency domain.''
Synthesis (Step 7)
The analysis portion of PARSHL returns a set of amplitudes
![]() , frequencies
, frequencies
![]() , and phases
, and phases
![]() ,
for each frame index
,
for each frame index ![]() , with a ``triad'' (
, with a ``triad'' (
![]() ) for each track
) for each track ![]() . From this analysis data the
program has the option of generating a synthetic sound.
. From this analysis data the
program has the option of generating a synthetic sound.
The synthesis is done one frame at a time. The frame at hop ![]() ,
specifies the synthesis buffer
,
specifies the synthesis buffer
![$\displaystyle s^m(n) = \sum_{r=1}^{R^m} \hat{A}_{r}^m \cos [n\hat{\omega}_{r}^m + \hat{\theta}_{r}^m]$](http://www.dsprelated.com/josimages_new/sasp2/img3081.png) |
(H.9) |
where
The parameter interpolation across time used in PARSHL is the same
as that used by McAulay and Quatieri [174]. Let
(
![]() ) and
(
) and
(
![]() ) denote the sets of
parameters at frames
) denote the sets of
parameters at frames ![]() and
and ![]() for the
for the ![]() th frequency track.
They are taken to represent the state of the signal at time 0
(the
left endpoint) of the frame.
th frequency track.
They are taken to represent the state of the signal at time 0
(the
left endpoint) of the frame.
The instantaneous amplitude
![]() is easily obtained by linear
interpolation,
is easily obtained by linear
interpolation,
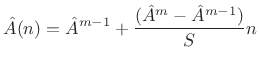 |
(H.10) |
where
Frequency and phase values are tied together (frequency is the phase
derivative), and they both control the instantaneous phase
![]() . Given that four variables are affecting the
instantaneous phase:
. Given that four variables are affecting the
instantaneous phase:
![]() , and
, and
![]() , we need at least
three degrees of freedom for its control, while linear interpolation
only gives one. Therefore, we need at least a cubic polynomial as
interpolation function, of the form
, we need at least
three degrees of freedom for its control, while linear interpolation
only gives one. Therefore, we need at least a cubic polynomial as
interpolation function, of the form
| (H.11) |
We will not go into the details of solving this equation since McAulay and Quatieri [174] go through every step. We will simply state the result:
| (H.12) |
where
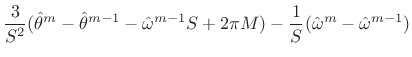 |
(H.13) | ||
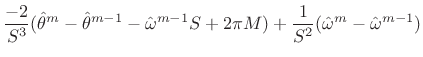 |
(H.14) |
This will give a set of interpolating functions depending on the value of
![$\displaystyle x= {1\over 2\pi} \left[(\hat{\theta}^{m-1} + \hat{\omega}^{m-1} S - \hat{\theta}^m) + (\hat{\omega}^m - \hat{\omega}^{m+1}) {S\over 2}\right]$](http://www.dsprelated.com/josimages_new/sasp2/img3096.png) |
(H.15) |
and finally, the synthesis equation turns into
![$\displaystyle s^m(n) = \sum_{r=1}^{R^m} \hat{A}_{r}^m(n) \cos [\hat{\theta}_{r}^m(n)]$](http://www.dsprelated.com/josimages_new/sasp2/img3097.png) |
(H.16) |
which smoothly goes from frame to frame and where each sinusoid accounts for both the rapid phase changes (frequency) and the slowly varying phase changes.
Figure H.5 shows the result of the analysis/synthesis process using phase information and applied to a piano tone.
![\includegraphics[width=\twidth]{eps/fig8}](http://www.dsprelated.com/josimages_new/sasp2/img3098.png) |
Magnitude-only Analysis/Synthesis
A traditional result of sound perception is that the ear is sensitive principally to the short-time spectral magnitude and not to the phase, provided phase continuity is maintained. Our experience has been that this may or may not be true depending on the application, and in §H.0.9 we will discuss it. Obviously if the phase information is discarded, the analysis, the modification, and the resynthesis processes are simplified enormously. Thus we will use the magnitude-only option of the program whenever the application allows it.
In the peak detection process we calculate the magnitude and phase of each peak by using the complex spectrum. Once we decide to discard the phase information there is no need for complex spectra and we simply can calculate the magnitude of the peak by doing the parabolic interpolation directly on the log magnitude spectrum.
The synthesis also becomes easier; there is no need for a cubic function to interpolate the instantaneous phase. The phase will be a function of the instantaneous frequency and the only condition is phase continuity at the frame boundaries. Therefore, the frequency can be linearly interpolated from frame to frame, like the amplitude. Without phase matching the synthesized waveform will look very different from the original (Fig.H.5), but the sound quality for many applications will be perceptually the same.
Preprocessing
The task of the program can be simplified and the analysis/synthesis results improved if the sound input is appropriately manipulated before running the program.
Most important is to equalize the input signal. This controls what it means to find spectral peaks in order of decreasing magnitude. Equalization can be accomplished in many ways and here we present some alternatives.
12pt
(1) A good equalization strategy for audio applications is to weight
the incoming spectrum by the inverse of the equal-loudness contour
for hearing at some nominal listening level (e.g., ![]() dB). This makes
spectral magnitude ordering closer to perceptual audibility ordering.
dB). This makes
spectral magnitude ordering closer to perceptual audibility ordering.
12pt (2) For more analytical work, the spectrum can be equalized to provide all partials at nearly the same amplitude (e.g., the asymptotic roll-off of all natural spectra can be eliminated). In this case, the peak finder is most likely to find and track all of the partials.
12pt (3) A good equalization for noise-reduction applications is to ``flatten'' the noise floor. This option is useful when it is desired to set a fixed (frequency-independent) track rejection threshold just above the noise level.
12pt (4) A fourth option is to perform adaptive equalization of types (2) or (3) above. That is, equalize each spectrum independently, or compute the equalization as a function of a weighted average of the most recent power spectrum (FFT squared magnitude) estimates.
Apart from equalization, another preprocessing strategy which has proven very useful is to reverse the sound in time. The attack of most sounds is quite ``noisy'' and PARSHL has a hard time finding the relevant partials in such a complex spectrum. Once the sound is reversed the program will encounter the end of the sound first, and since in most instrumental sounds this is a very stable part, the program will find a very clear definition of the partials. When the program gets to the sound attack, it will already be tracking the main partials. Since PARSHL has a fixed number of oscillators which can be allocated to discovered tracks, and since each track which disappears removes its associated oscillator from the scene forever,H.3 analyzing the sound tail to head tends to allocate the oscillators to the most important frequency tracks first.
Applications
The simplest application of PARSHL is as an analysis tool since we can get a very good picture of the evolution of the sound in time by looking at the amplitude, frequency and phase trajectories. The tracking characteristics of the technique yield more accurate amplitudes and frequencies than if the analysis were done with an equally spaced bank of filters (the traditional STFT implementation).
In speech applications, the most common use of the STFT is for data-reduction. With a set of amplitude, frequency and phase functions we can get a very accurate resynthesis of many sounds with much less information than for the original sampled sounds. From our work it is still not clear how important is the phase information in the case of resynthesis without modifications, but McAulay and Quatieri [174] have shown the importance of phase in the case of speech resynthesis.
Some of the most interesting musical applications of the STFT techniques are given by their ability to separate temporal from spectral information, and, within each spectrum, pitch and harmonicity from formant information. In §H.0.5, Parameter Modifications, we discussed some of them, such as time scaling and pitch transposition. But this group of applications has a lot of possibilities that still need to be carefully explored. From the few experiments we have done to date, the tools presented give good results in situations where less flexible implementations do not, namely, when the input sound has inharmonic spectra and/or rapid frequency changes.
The main characteristic that differentiates this model from the traditional ones is the selectivity of spectral information and the phase tracking. This opens up new applications that are worth our attention. One of them is the use of additive synthesis in conjunction with other synthesis techniques. Since the program allows tracking of specific spectral components of a sound, we have the flexibility of synthesizing only part of a sound with additive, synthesis, leaving the rest for some other technique. For example, Serra [247] has used this program in conjunction with LPC techniques to model bar percussion instruments, and Marks and Polito [163] have modeled piano tones by using it in conjunction with FM synthesis [38]. David Jaffe has had good success with birdsong, and Rachel Boughton used PARSHL to create abstractions of ocean sounds.
One of the problems encountered when using several techniques to synthesize the same sound is the difficulty of creating the perceptual fusion of the two synthesis components. By using phase information we have the possibility of matching the phases of the additive synthesis part to the rest of the sound (independently of what technique was used to generate it). This provides improved signal ``splicing'' capability, allowing very fast cross-fades (e.g., over one frame period).
PARSHL was originally written to properly analyze the steady state of piano sounds; it did not address modeling the attack of the piano sound for purposes of resynthesis. The phase tracking was primarily motivated by the idea of splicing the real attack (sampled waveform) to its synthesized steady state. It is well known that additive synthesis techniques have a very hard time synthesizing attacks, both due to their fast transition and their ``noisy'' characteristics. The problem is made more difficult by the fact that we are very sensitive to the quality of a sound's attack. For plucked or struck strings, if we are able to splice two or three periods, or a few milliseconds, of the original sound into our synthesized version the quality can improve considerably, retaining a large data-reduction factor and the possibility of manipulating the synthesis part. When this is attempted without the phase information, the splice, even if we do a smooth cross-fade over a number of samples, can be very noticeable. By simply adding the phase data the task becomes comparatively easy, and the splice is much closer to inaudible.
Conclusions
In this appendix, an analysis/synthesis technique based on a sinusoidal representation was presented that has proven to be very appropriate for signals which are well characterized as a sum of inharmonic sinusoids with slowly varying amplitudes and frequencies. The previously used harmonic vocoder techniques have been relatively unwieldy in the inharmonic case, and less robust even in the harmonic case. PARSHL obtains the sinusoidal representation of the input sound by tracking the amplitude, frequency, and phase of the most prominent peaks in a series of spectra computed using a Cooley-Tukey Fast Fourier Transform (FFT) of successive, overlapping, windowed data frames, taken over the duration of a sound. We have mentioned some of the musical applications of this sinusoidal representation.
Continuing the work with this analysis/synthesis technique we are implementing PARSHL on a Lisp Machine with an attached FPS AP120B array processor. We plan to study further its sound transformation possibilities and the use of PARSHL in conjunction with other analysis/synthesis techniques such as Linear Predictive Coding (LPC) [162].
The basic ``FFT processor'' at the heart of PARSHL provides a ready point of departure for many other STFT applications such as FIR filtering, speech coding, noise reduction, adaptive equalization, cross-synthesis, and many more. The basic parameter trade-offs discussed in this appendix are universal across all of these applications.
Although PARSHL was designed to analyze piano recordings, it has proven very successful in extracting additive synthesis parameters for radically inharmonic sounds. It provides interesting effects when made to extract peak trajectories in signals which are not describable as sums of sinusoids (such as noise or ocean recordings). PARSHL has even demonstrated that speech can be intelligible after reducing it to only the three strongest sinusoidal components.
The surprising success of additive synthesis from spectral peaks suggests a close connection with audio perception. Perhaps timbre perception is based on data reduction in the brain similar to that carried out by PARSHL. This data reduction goes beyond what is provided by critical-band masking. Perhaps a higher-level theory of ``timbral masking'' or ``main feature dominance'' is appropriate, wherein the principal spectral features serve to define the timbre, masking lower-level (though unmasked) structure. The lower-level features would have to be restricted to qualitatively similar behavior in order that they be ``implied'' by the louder features. Another point of view is that the spectral peaks are analogous to the outlines of figures in a picture--they capture enough of the perceptual cues to trigger the proper percept; memory itself may then serve to fill in the implied spectral features (at least for a time).
Techniques such as PARSHL provide a powerful analysis tool toward extracting signal parameters matched to the characteristics of hearing. Such an approach is perhaps the best single way to obtain cost-effective, analysis-based synthesis of any sound.
Acknowledgments
The authors of [271] thank Dynacord, Inc., for supporting the development of the first version of PARSHL in the summer of 1985. We also wish to acknowledge the valuable contributions of Gerold Schrutz (of Dynacord) during that time.
Software Listing
The software listing below is in the SAIL programming language (generally a superset of ALGOL). Since procedures are defined before they are used, the listing starts out defining basic utilities, progressing to higher levels until finally the top level is reached. As a result, it is usually easier start read the top level procedure at the end first, and then work backwards to fill in the details.
The SAIL keyboard had various non-standard characters which are spelled out here using TeX equivalents such as &alpha#alpha; and &beta#beta;.
COMMENT Track instantaneous amplitudes and frequencies of multiple sinusoids; COMMENT Side-result: FFT-based filtering and/or inharmonic additive synthesis; COMMENT Completed in the summer of 1985 by Julius O. Smith III BEGIN "PARSHL" REQUIRE "{}<>" DELIMITERS; DEFINE #="comment",CrLf="'15&'12",tab={""&'11},Sam16="4",Cr="'15", ALT={'175&""},Thru={step 1 until}; REQUIRE "JOSLIB.REQ[LIB,JOS]" SOURCE!FILE; REQUIRE "REQUIRING UDP2:SIGLIB.REL[SIG,MUS] LIBRARY" MESSAGE; REQUIRE "UDP2:SIGLIB.REL[SIG,MUS]" LIBRARY; REQUIRE "JAMLIB.REL[SUB,SYS]" LIBRARY; REQUIRE "TRMTYP.SAI[LIB,JOS]" SOURCE!FILE; REQUIRE "DISPLA.REQ[LIB,JOS]" SOURCE!FILE; EXTERNAL PROCEDURE TRPINI(INTEGER CODE); # Enable floating point exception code; EXTERNAL PROCEDURE SUPCT; # Disable \alpha-I,\alpha-R,\alpha-T,\alpha-L etc; REQUIRE "RECORD.REQ[LIB,JOS]" SOURCE!FILE; # REQUIRE "MYIO.REQ[LIB,JOS]" SOURCE!FILE; COMMENT Declare File IO stuff; REQUIRE "FLTIO.REQ[LIB,JOS]" SOURCE!FILE; COMMENT Declare GetFlt; EXTERNAL BOOLEAN PROCEDURE AinInt(REFERENCE INTEGER Val; STRING Name); EXTERNAL BOOLEAN PROCEDURE AinReal(REFERENCE REAL Val; STRING Name); EXTERNAL STRING PROCEDURE Cvfs(REAL Val); EXTERNAL SIMPLE BOOLEAN PROCEDURE FNparse( STRING Arg; REFERENCE STRING Device; REFERENCE STRING Filename); EXTERNAL STRING PROCEDURE DEV(STRING Name); COMMENT Return DEVICE part of filename; EXTERNAL STRING PROCEDURE NAME(STRING Name); COMMENT Return NAME part of filename; EXTERNAL STRING PROCEDURE EXT(STRING Name); COMMENT Return extension part of filename; EXTERNAL STRING PROCEDURE PPN(STRING Name); COMMENT Return PPN part of filename; COMMENT SOUND IO DECLARATIONS; REQUIRE "SYS:DEFAUL.HDR" SOURCE!FILE; # REQUIRE "RHEAD.REL[SYS,MUS]" LOAD!MODULE; # REQUIRE "WHEAD.REL[SYS,MUS]" LOAD!MODULE; EXTERNAL BOOLEAN PROCEDURE SANDI( INTEGER Chan, StSamp, Nsamps; REFERENCE REAL ARRAY X; INTEGER FilSamps, Headed, FilPak, Xpack(-1)); EXTERNAL BOOLEAN PROCEDURE SANDO( INTEGER Chan, StSamp, Nsamps; REFERENCE REAL ARRAY X; REFERENCE INTEGER ARRAY Hist; REFERENCE INTEGER FilSamps; INTEGER Headed, FilPak, Xpack(-1)); # ReadH (rp, hdbuf, Fail, true if don't want printout); EXTERNAL PROCEDURE ReadH ( RECORD!POINTER (File) Rp; REFERENCE REAL ARRAY Hdbuf; REFERENCE INTEGER FAIL; BOOLEAN Silence (FALSE)); # WriteH (head, clock, pack, #chans, #ticks, maxamp, cstr); EXTERNAL PROCEDURE WriteH ( REFERENCE REAL ARRAY Head; REAL Clock; INTEGER Pack, #chans, #ticks; REAL Maxamp; STRING Cstr ); INTEGER ARRAY OutH,AmpH,FrqH[0:128]; REAL ARRAY Head[1:128]; INTEGER Nread,Brk; REAL Maxamp; BOOLEAN FAIL,Eof; STRING Ifile,Idev,Ofile,Odev; STRING AmpFile,AmpDev,FrqFile,FrqDev,Tstr; RECORD!POINTER (File) InFptr, OutFptr; RECORD!POINTER (File) AmpFptr, FrqFptr; DEFINE InF(x) = {File:x[InFptr]}, OutF(x) = {File:x[OutFptr]}; DEFINE AmpF(x) = {File:x[AmpFptr]}, FrqF(x) = {File:x[FrqFptr]}; COMMENT Filter input; # REQUIRE "JOSLIB.REQ[LIB,JOS]" SOURCE!FILE; # REQUIRE "RECORD.REQ[LIB,JOS]" SOURCE!FILE; # REQUIRE "FLTIO.REQ[LIB,JOS]" SOURCE!FILE; COMMENT Declare GetFlt; DEFINE MaxCoeffs = "8192"; COMMENT Maximum number of filter coefficients; STRING Ffile; INTEGER Ni,No; REAL ARRAY Ic,Oc[1:MaxCoeffs]; INTEGER Nfft,Nspec,Nh,Nx,Nhop,Ndec,i,Nhops; INTERNAL INTEGER Trace; DEFINE ShowSpectra="(Trace LAND 1)"; DEFINE TDpyFFA = " IF ShowSpectra THEN DpyFFA "; DEFINE ShowTime="(Trace LAND 2)"; DEFINE TDpyEd = " IF ShowTime THEN DpyEd "; DEFINE ShowPeakFinder="(Trace LAND 4)"; DEFINE Debug1="(Trace LAND 8)", Debug2="(Trace LAND 16)", Debug3="(Trace LAND 32)"; BOOLEAN HaveOfile,HaveIfile,HaveFfile,HavePack; STRING TmpStr; EXTERNAL INTEGER !SKIP!; IFC FALSE THENC # SAIL Esc-I interrupt facility; SIMPLE PROCEDURE EscI; # This is called upon <esc>I interrupt; START!CODE "EscI" TLZE '10,'400000; # If sign bit is on; MOVN '10,'10; # Convert sign-magnitude to 2' comp; MOVEM '10, Trace; # Save Ac 10; CALLI 0, '400024; # DISMIS (return to user level); END "EscI"; PROCEDURE Int!init; BEGIN EXTERNAL INTEGER JOBAPR; # JOB DATA AREA user interrupt routine pointer; JOBAPR <- LOCATION(EscI); ENABLE(15); # Enable user interrupt handling; Trace <- 0; END; COMMENT REQUIRE Int!Init INITIALIZATION; COMMENT rmoved by BIL because he thinks this is extremely dangerous -- you are depending on getting only esc-i interrupts and nothing else. The SAIL runtime world that tries to handle arithmetic exceptions (for example) depends on JOBAPR pointing to some procedure that can handle such interrupts (UDP2:TRIGS[NEW,SAI]/4P and UDP2:NWORLD[NEW,SAI]/31,32P); ELSEC IFC NOT DECLARATION(GOGTAB) THENC EXTERNAL INTEGER ARRAY GOGTAB[0:'300]; ENDC SIMPLE PROCEDURE Esci; Trace <- GOGTAB['200]; PROCEDURE Int!Init; BEGIN ENABLE(15); INTMAP(15,Esci,0); Trace <- 0; END; REQUIRE Int!Init INITIALIZATION; ENDC # Global declarations; BOOLEAN DoFlt,DoSynth,DoOut,SwapOut; # Flags for type of function wanted; REAL MinSep,Thresh,Hyst,DFmax1,DFmax2,DAmax,SigScl,Fc1,Fc2,Fs,DBscl; INTEGER MaxLins,MaxOscs,Nframes,Npartials,Frame,MinWid; BOOLEAN Quiet,InstantRise; COMMENT DerivedName - Generate name from root name and code string; STRING PROCEDURE DerivedName(STRING GivenName, CodeString); BEGIN "DerivedName" INTEGER i,j,ln,lc; STRING Gname,DevStr; STRING RootName; # REQUIRE "JOSLIB.REQ[LIB,JOS]" SOURCE!FILE; EXTERNAL STRING PROCEDURE DEV(STRING Name); COMMENT Return DEVICE part of filename; EXTERNAL STRING PROCEDURE NAME(STRING Name); COMMENT Return NAME part of filename; EXTERNAL STRING PROCEDURE EXT(STRING Name); COMMENT Return extension part of filename; EXTERNAL STRING PROCEDURE PPN(STRING Name); COMMENT Return PPN part of filename; Gname <- NAME(GivenName); ln <- LENGTH(Gname); lc <- LENGTH(CodeString); IF lc+ln LEQ 6 THEN RootName <- Gname&CodeString ELSE RootName <- Gname[1 to 6-lc]&CodeString; IF EQU(RootName,Gname) THEN BEGIN # Gak! Must generate a new name!; PRINT(" DerivedName got a name collision",CrLf); IF ln>1 THEN RootName <- Gname[1 to 6-lc-1]&CodeString&"2" ELSE RootName <- Gname[1 to 6-lc]&CodeString[1 to lc-1]&"2"; IF EQU(RootName,Gname) THEN RootName <- RootName[1 to 5]&"3"; END; DevStr <- Dev(GivenName); IF DevStr NEQ NULL THEN DevStr <- DevStr&":"; RETURN(DevStr&RootName&Ext(GivenName)&Ppn(GivenName)); END "DerivedName"; COMMENT Fprint - Print documentation from DSK; # Put this in JOSLIB; PROCEDURE Fprint(STRING Fname); COMMENT Print contents of file in fname; BEGIN STRING Help,Ttystr; INTEGER Fchan,Brk,Eof,Bt; BOOLEAN FAIL; DEFINE FF={('14&"")}; OPEN(Fchan <- GETCHAN,"DSK",0,2,0,2000,Brk,Eof); COMMENT Ascii input; LOOKUP(Fchan,Fname,FAIL); IF FAIL THEN USERERR(0,1," Can't find HELP file "&Fname); IF FAIL THEN RETURN; SETBREAK(Bt <- GETBREAK,FF,NULL,"sin"); DO BEGIN "pages" Help <- INPUT(Fchan,Bt); IF NOT EQU(Help[1 FOR 7],"COMMENT") THEN BEGIN MyOutDpy(Help,-3,-1); MyOutDpy ("Type RETURN to continue - ALT to return to command level",31,-1); MyOutDpy (Fname,33,-1); Ttystr <- INCHWL; Break!N; IF Ttystr="H" OR Ttystr = "?" THEN MyOutDpy(" This IS help!!",32,-1); IF !skip!="H" OR !skip! = "?" THEN MyOutDpy(" This IS help!!",32,-1); IF !skip! = ALT THEN BEGIN PRINT(CrLf); DONE "pages"; END; END; END "pages" UNTIL Eof; Relbreak(Bt); RELEASE(Fchan); END; COMMENT Help - Command Summaries; RECURSIVE PROCEDURE HELP(STRING Topic(NULL)); BEGIN "help" Break!N; IF EQU(Topic,"?") THEN BEGIN Fprint("PARSHL.JOS[MUS,DOC]"); PRINT(CrLf,CrLf," Type \alpha-? for command summary",CrLf); # PRINT(" Type <command!letter>\alpha-? for individual command description",CrLf); PRINT(" Type ?\alpha-? or ?,?<RETURN> for full documentation",CrLf,CrLf); RETURN; END; IF EQU(Topic,"TopLevel") THEN MyOutDpy(" Outer Level Command Summary [s> => string, [n> => integer, [d> => real number, \alpha- => CONTROL, and \beta- => META ALT - Exit PARSHL. ?\alpha-? - Print complete documentation. (Also ?,?[CR> does this.) [n>\alpha-W - Analysis Window (1=rect,2=triang,3:5=Hamming,6=Kaiser,7=Cheb) [n>\alpha-T - FFT length (must be a power of 2). [n>\alpha-D - Number of samples of input signal per FFT frame. [n>\alpha-H - Number of samples of input signal to advance between FFT's. [n>\alpha-L - Length of filter impulse response (if known). [n>\alpha-C - Decimation factor (1 => no decimation, 2 => every other sample, etc.) [s>\alpha-I - Input sound file. [s>\alpha-O - Output sound file. [n>\alpha-P - Output sound file packing mode. (\alpha-P with no arg explains codes.) [s>\alpha-F - Input filter file. ; - Comment. [ESC>[n>I codes: (n can be any sum of the following): [n> display(s) enabled --- ------------------ 0 none (type [ESC>I to turn off all running displays) 1 time buffers ([ESC>1I) 2 spectral buffers ([ESC>2I) 4 peak-finder 8 debug level 1 16 debug level 2 32 debug level 3 ------------------------------------------------------------------------ ",-3,-1); IF EQU(Topic,"SubLevel") THEN MyOutDpy(" Inner Level Command Summary [s] => string, [n] => integer, [d] => real number, \alpha- => CONTROL, and \beta- => META ALT - Exit to Outer level. ?\alpha-? - Print complete documentation. (Also ?,?[CR] does this.) [d]\alpha-M - Minimum spacing between partials in Hz [n]\alpha-N - Maximum number of partials to track [n]\alpha-O - Maximum number of oscillators to use [d]\alpha-F - First (lowest) partial frequency allowed (Hz) [d]\alpha-L - Last (highest) partial frequency allowed (Hz) [d]\alpha-T - Peak detection threshold in dB [d]\alpha-H - Spectral wiggle tolerance in dB [d]\alpha-D - Maximum allowed frequency deviation per frame in Hz at LOW frequency [d]\alpha-U - Maximum allowed frequency deviation per frame in Hz at HIGH frequency [n]\alpha-B - Buffer display code. If negative, all time buffers are displayed. \alpha-S - Show spectra of filter input and output on each FFT hop. (\beta-S disables.) ; - Comment. ------------------------------------------------------------------------ ",-3,-1); END "help"; COMMENT DpyFFA - Display interleaved dB spectra as computed by FFA in SIGLIB; PROCEDURE DpyFFA(REAL ARRAY S; INTEGER Nfft; STRING T; REAL Fs(1)); COMMENT For displaying interleaved dB spectra as computed by FFA in SIGLIB; BEGIN "DpyFFA" INTEGER i,Nspec; REAL ARRAY Spec[1:(Nfft DIV 2)+1]; Nspec <- (Nfft DIV 2) + 1; FOR i <- 1 STEP 1 UNTIL Nspec DO Spec[i] <- (10.0/LOG(10.0))*LOG( (S[2*i-1]^2+S[2*i]^2) MAX 1.0@-35); DpyEd(Spec,Nspec,T,"MAGNITUDE (DB)",0,Fs/2); END "DpyFFA"; COMMENT Qinterp - Quadratic interpolation; INTERNAL SIMPLE REAL PROCEDURE Qinterp(REAL Ym1,Y0,Yp1; BOOLEAN InteriorX(TRUE)) ; COMMENT Fit a parabola Y[X] = A*X^2+B, through the three equally spaced Y-values Ym1 = Y[-1], Y0 = Y[0], and Yp1=Y[1], and return the X-value where the extremum is attained. For example, if -1 is returned, then Y[-1] is the point of zero slope in the parabola through the three points. If InteriorX is TRUE then if the extremum lies outside the interval [-1,1], a warning is printed and the returned value is clipped to lie at either 1 or -1 as appropriate. ; BEGIN "Qinterp" REAL X; X <- (Yp1 - Ym1)/(2*(2*Y0 - Yp1 - Ym1)); IF InteriorX AND (ABS(X)>1) THEN PRINT(" Qinterp: Clipping analytic extremum to ", X <- (IF X>0 THEN 1 ELSE -1),CrLf); IF Debug3 THEN PRINT("Qinterp: Given Y's ",Ym1," ",Y0," ",Yp1, ", extremum is at X = ",X,CRLF); RETURN(X); END "Qinterp"; COMMENT FindPeaks - Generic peak finder; IFC NOT DECLARATION(IntNoSet) THENC DEFINE IntNoSet={(1 LSH 35)}; IFC NOT DECLARATION(RealNoSet) THENC DEFINE RealNoSet={(-1.0@35)}; INTEGER PROCEDURE FindPeaks(REAL ARRAY X,Peaks,PeakLocs; REAL Thresh(RealNoSet),Hyst(RealNoSet); INTEGER MaxPeaks(IntNoSet),MinWidth(IntNoSet),BlankWidth(IntNoSet), I1(IntNoSet),I2(IntNoSet)); COMMENT Find amplitudes and indices of all peaks in X = array of values to be searched for peaks. (It is overwritten.) Peaks[1:MaxPeaks] = peak amplitudes. PeakLocs[1:MaxPeaks] = peak indices. Thresh = Threshold below which no peaks are to be sought Hyst = Wiggles less than Hyst in magnitude are ignored. MaxPeaks = Maximum number of peaks to be found (starting w largest) MinWidth = Minimum peak width in indices, after blanking. Narrower peaks are removed and ignored. BlankWidth = Minimum blanking interval in indeces. If = IntNoSet, then blank to nearest local minimum to within Hyst interval. Blanking is done before width is measured for efficiency reasons (would rather measure width first). i1,i2 = index boundaries for the search within X. The return value is the number of peaks actually found. ; BEGIN "FindPeaks" INTEGER i,j,Npeaks,NdxReach,Owid,Odig,Peak,Poff,PLoff,M1,M2,Nfound,Lb,Ub; REAL Xmax,Xmin; GETFORMAT(Owid,Odig); SETFORMAT(0,5); NdxReach <- (IF (BlankWidth NEQ IntNoSet) THEN (BlankWidth-1)/2 MAX 1 ELSE 0); Poff <- ARRINFO(Peaks,1)-1; PLoff <- ARRINFO(PeakLocs,1)-1; Npeaks <- (IF MaxPeaks NEQ IntNoSet THEN MaxPeaks ELSE ARRINFO(Peaks,2)-Poff); Npeaks <- Npeaks MIN (ARRINFO(Peaks,2)-Poff) MIN (ARRINFO(PeakLocs,2)-PLoff); Lb <- ARRINFO(X,1); Ub <- ARRINFO(X,2); IF I2=IntNoSet THEN I2 <- ARRINFO(X,2); IF I1=IntNoSet THEN I1 <- ARRINFO(X,1); I1 <- (Lb MAX I1 MIN Ub); I2 <- (I1 MAX I2 MIN Ub); ArrMin(Xmin,X,I1,I2); ArrMax(Xmax,X,I1,I2); IF Thresh=RealNoSet THEN Thresh <- Xmin; IF Hyst=RealNoSet THEN Hyst <- (Xmax-Xmin)/100; M1 <- M2 <- 0; COMMENT [m1,m2] = index interval of last peak; Nfound <- 0; FOR Peak <- 1 STEP 1 UNTIL Npeaks DO BEGIN "fp" INTEGER MaxLoc,TmpI; REAL MaxVal,ClobVal,TmpR; IF M1=I1 AND M2=I2 THEN DONE "fp"; MaxLoc <- ArrMax(MaxVal,X,I1,I2); IF MaxVal<Thresh THEN DONE "fp"; Nfound <- Nfound + 1; PeakLocs[Nfound+PLoff] <- MaxLoc + Qinterp(X[(MaxLoc-1) MAX I1],MaxVal,X[(MaxLoc+1) MIN I2]); IF MaxLoc=I1 AND Debug1 THEN PRINT("*** Peak is at right of search interval for peak ",Nfound," ***",CrLf); IF MaxLoc=I2 AND Debug1 THEN PRINT("*** Peak is at left of search interval for peak ",Nfound," ***",CrLf); Peaks[Nfound+Poff] <- MaxVal; COMMENT Now slice off peak so we don't find it again; M1 <- (MaxLoc-NdxReach) MAX I1; M2 <- (MaxLoc+NdxReach) MIN I2; ArrMin(ClobVal,X,M1,M2); TmpR <- X[M1]; WHILE M1>I1 AND TmpR+Hyst GEQ X[M1-1] DO BEGIN TmpR <- TmpR MIN X[M1-1]; M1 <- M1-1 END; ClobVal <- ClobVal MIN TmpR; TmpR <- X[M2]; WHILE M2<I2 AND TmpR+Hyst GEQ X[M2+1] DO BEGIN TmpR <- TmpR MIN X[M2+1]; M2 <- M2+1 END; ClobVal <- ClobVal MIN TmpR; FOR i <- M1 STEP 1 UNTIL M2 DO X[i] <- ClobVal; IF (M2-M1+1 < MinWidth) OR MaxLoc=I1 OR MaxLoc=I2 # JOS/10/25/85; THEN BEGIN "Throw it back" Nfound <- Nfound-1; CONTINUE "fp"; END "Throw it back"; IF ShowPeakFinder THEN DpyEd(X,I2-ARRINFO(X,1)+1,"X remains after peak "& CVS(Nfound)&" at i="&CVS(MaxLoc)); END "fp"; SETFORMAT(Owid,Odig); RETURN(Nfound); END "FindPeaks"; COMMENT FindPartials - Find all significant spectral lines for current frame; PROCEDURE FindPartials(REFERENCE INTEGER Npartials; REAL ARRAY XmagDB,LinAmp,LinFrq; REAL Fs,MinSep,Thresh,Hyst; INTEGER Nfft,Frame,MinWid; REAL Fc1(RealNoSet),Fc2(RealNoSet)); COMMENT Find amplitudes (dB) and frequencies (Hz) of all partials in XmagDB. Npartials = the maximum number of partials to find. It is set to the actual number of partials found on return. XmagDB[1:Nfft/2+1] = DB magnitude spectrum LinAmp[1:Nharms,1:Nframes] = Partial amplitudes LinFrq[1:Nharms,1:Nframes] = Partial frequencies Fs = sampling rate (Hz) MinSep = minimum line spacing (Hz) Thresh,Hyst are args to FindPeaks Nfft = Size of FFT used in computing XmagDB Frame = current time frame number MinWid = minimum acceptable peak width in FFT bins. Fc1,Fc2 = lower and upper frequency bounds in Hz. No partials will be allowed outside this interval. ; BEGIN "FindPartials" REQUIRE "HACKS.REL[SUB,SYS]" LIBRARY; EXTERNAL SIMPLE PROCEDURE QISort(REAL ARRAY A,Data; INTEGER LB,UB); INTEGER i,j,Nspec,BinInt,BinReach,Owid,Odig,Partial,MinWid; REAL ARRAY Xsave[1:Nspec <- Nfft/2+1]; GETFORMAT(Owid,Odig); SETFORMAT(0,7); BinInt <- (MinSep/Fs)*Nfft+.5; # Blanking interval for spectral peak (in bins); IF Frame=1 THEN PRINT(CrLf," Blanking interval is ",BinInt," bins",CrLf); ARRTRAN(Xsave,XmagDB); # Save input array; Npartials <- FindPeaks(XmagDB,LinAmp,LinFrq,Thresh,Hyst, Npartials,MinWid,BinInt,((1+Nfft*Fc1/Fs) MAX 1),((1+Nfft*Fc2/Fs) MIN Nspec)); ARRTRAN(XmagDB,Xsave); # Sort for ascending frequency (for convenience only); IF Npartials>0 THEN QIsort(LinFrq,LinAmp,1,Npartials); IF Debug2 THEN PRINT(CrLf); FOR Partial <- 1 STEP 1 UNTIL Npartials DO BEGIN "fp" LinFrq[Partial] <- Fs*(LinFrq[Partial]-1)/Nfft; IF Debug2 GEQ Partial THEN PRINT("Frame=",Frame," Amp(dB)=",LinAmp[Partial], " Freq(Hz)=",LinFrq[Partial],"=",Partial,"*",MinSep,"*", LinFrq[Partial]/(Partial*MinSep),CrLf); END "fp"; IF ShowPeakFinder THEN BEGIN "ShowHarms" REAL ARRAY CFrqs[1:Nspec]; REAL Val; Val <- LinAmp[1]; j <- 1; FOR Partial <- 1 STEP 1 UNTIL Npartials DO BEGIN FOR i <- j STEP 1 UNTIL Nfft*(LinFrq[Partial]/Fs) DO CFrqs[i] <- Val; j <- i; Val <- LinAmp[Partial]; END; Dpy2(XmagDB,CFrqs,i, "Centers of pitch-wide search regions for frame "&CVS(Frame), "MAGNITUDE (DB)",0,Fs/2,-30,30); END "ShowHarms"; SETFORMAT(Owid,Odig); END "FindPartials"; COMMENT OutPartials - Write partial amplitudes and frequencies to disk; PROCEDURE OutPartials(INTEGER Npartials,Nframes; REAL ARRAY Amps,Frqs; REAL Fs,Thresh); BEGIN "OutPartials" INTEGER N,AmpP,FrqP; N <- Npartials*Nframes; Sando(AmpF(Channel),AmpP,N,Amps,AmpH,AmpP,TRUE,AmpF(Pack)); Sando(FrqF(Channel),FrqP,N,Frqs,FrqH,FrqP,TRUE,FrqF(Pack)); Sando(AmpF(Channel),0,0,Amps,AmpH,AmpP,TRUE,AmpF(Pack)); Sando(FrqF(Channel),0,0,Frqs,FrqH,FrqP,TRUE,FrqF(Pack)); END "OutPartials"; COMMENT Decimate - Downsample by integer factors; INTEGER PROCEDURE Decimate(REAL ARRAY A; INTEGER N,M,I(0)); COMMENT Downsample array A[1:N] by M. I nonzero means initialize; COMMENT Return the number of samples produced; BEGIN "Decimate" OWN INTEGER P; INTEGER j; IF M LEQ 1 THEN RETURN(N); IF I NEQ 0 OR P LEQ 0 THEN P <- 1; j <- 0; FOR i <- P STEP M UNTIL N DO A[j <- j+1] <- A[i]; P <- i-N; RETURN(j); END "Decimate"; COMMENT GetWin - Compute overlap-add analysis window; INTEGER WinType; DEFINE Rectangular="1", Triangular="2", Hamming="3", GenHamming="4", Hanning="5", Kaiser="6", Chebyshev = "7", Nwins = "7"; PRELOAD!WITH "Rectangular", "Triangular", "Hamming", "GenHamming", "Hanning", "Kaiser", "Chebyshev"; STRING ARRAY WinNames[1:Nwins]; DEFINE WinStr = "WinNames[WinType]"; PROCEDURE GetWin(REAL ARRAY W; INTEGER Wtype,Nw; REAL P3(-1.),P4(-1.)); COMMENT Generate analysis window taking special care to ensure that it will overlap-add to unity in the case of a Hamming window with hopsize = Nw/(2K) Wtype Window ----- ------ 1 Rectangular 2 Triangular 3 Hamming 4 Generalized Hamming 5 Hanning 6 Kaiser 7 Chebyshev ; BEGIN "GetWin" # REQUIRE "SIGLIB.REL[SUB,SYS]" LIBRARY; EXTERNAL PROCEDURE !WINFLT(REAL ARRAY H; REFERENCE INTEGER NH; REFERENCE INTEGER WINTYP; REFERENCE INTEGER BNDTYP; REAL ARRAY P); REAL ARRAY WinPars[1:4]; WinPars[1] <- 0; # Lower cutoff frequency; WinPars[2] <- 0; # Upper cutoff frequency; IF WinType=Kaiser AND P3<0 THEN DO BEGIN IF NOT AinReal(P3 <- 60,"Kaiser stop-band rejection in DB") THEN RETURN; IF P3 < 0 THEN PRINT("Stop-Band rejection must be POSITIVE dB...like 60",CRLF); END UNTIL P3 GEQ 0; IF WinType=GenHamming AND P3<0 THEN DO IF NOT AinReal(P3 <- 0.54,"Alpha (0:4)") THEN RETURN UNTIL (0 LEQ P3 LEQ 4); IF WinType=Chebyshev AND P4 LEQ 0 THEN DO BEGIN "GetCheb" IF NOT AinReal(P3, "Chebyshev stop-band rejection in DB (or minus transition width in Hz/Srate)") THEN RETURN; IF P3<0 THEN BEGIN P4 <- P3; P3 <- 0; END ELSE P4 <- 0; END "GetCheb" UNTIL (0 LEQ P4<1/2 AND 0 LEQ P3); WinPars[3] <- P3; WinPars[4] <- P4; IF (Nw MOD 2) = 1 THEN BEGIN REAL ARRAY TmpBuf[1:2*Nw+1]; !WinFlt(TmpBuf,Nw,Wtype,1,WinPars); # Analysis window = lowpass, Fc=0; ARRTRAN(W,TmpBuf); IF Wtype>Rectangular THEN W[Nw] <- 0; # For odd lengths, last sample zeroed; END ELSE BEGIN REAL ARRAY TmpBuf[1:2*Nw+1]; INTEGER i; !WinFlt(TmpBuf,i <- 2*Nw+1,Wtype,1,WinPars); FOR i <- 1 STEP 1 UNTIL Nw DO W[i] <- TmpBuf[2*i]; END; BEGIN "nrmlz" # REQUIRE "JOSLIB.REQ[LIB,JOS]" SOURCE!FILE; EXTERNAL REAL PROCEDURE MaxArr(INTEGER n; REAL ARRAY y); INTEGER i; REAL Wmax,Wscl; Wmax <- MaxArr(Nw,W); Wscl <- 1.0/Wmax; FOR i <- 1 STEP 1 UNTIL Nw DO W[i] <- W[i]*Wscl; END "nrmlz"; Tdpyed(W,Nw,"GETWIN: Window returned"); END "GetWin"; BOOLEAN PROCEDURE GetIfile(STRING IfileTry); BEGIN "GetIfile" DO BEGIN FNparse(IfileTry,Idev,Ifile); PRINT(Tab,"Reading file ",Idev,":",Ifile,Crlf); RELEASE(InF(Channel)); OPEN(InF(Channel) <- GETCHAN,Idev,'17,0,0,200,Brk,Eof); LOOKUP(InF(Channel),Ifile,FAIL); IF FAIL THEN BEGIN PRINT("File not found",CrLf); PRINT("Input sound file: "); IfileTry <- INCHWL; IF !SKIP!=ALT THEN RETURN(FALSE); END ELSE BEGIN ReadH(InFptr,Head,FAIL,Quiet); # Read and print header; InF(Name) <- Ifile; END END UNTIL NOT FAIL; RETURN(TRUE); END "GetIfile"; BOOLEAN PROCEDURE GetOfile(STRING OfileTry); BEGIN "GetOfile" DO BEGIN Ofile <- OfileTry; FNparse(OfileTry,Odev,Ofile); PRINT(Tab,"Writing file ",Odev,":",Ofile,Crlf); RELEASE(OutF(Channel)); OPEN(OutF(Channel) <- GETCHAN,Odev,'17,0,0,200,Brk,Eof); ENTER(OutF(Channel),Ofile,FAIL); IF FAIL THEN BEGIN PRINT("Can't ENTER output file",CrLf); PRINT("Output sound file: "); OfileTry <- INCHWL; IF !SKIP!=ALT THEN RETURN(FALSE); END ELSE HaveOfile <- TRUE; END UNTIL NOT FAIL; RETURN(TRUE); END "GetOfile"; COMMENT Get user input parameters; SUPCT; # Disable \alpha-IC,\alpha-T,\alpha-L; TTYUP(TRUE); # Convert to upper case on input; TrpIni('26); # all except integer overflow (1) and real uflow ('10); # The following is apparently too severe: TRPINI(-1); # Enable decent floating point exception code; Find!Type; # Get terminal characteristics; Quiet <- (IF dpytype=ddtype THEN FALSE ELSE TRUE); PRINT(CrLf,"PARSHL: ", COMPILER!BANNER[LENGTH(SCANC(COMPILER!BANNER,Tab,"","sinz"))+11 FOR 17],CrLf); InFptr <- NEW!RECORD (File); OutFptr <- NEW!RECORD (File); AmpFptr <- NEW!RECORD (File); FrqFptr <- NEW!RECORD (File); BEGIN "GetPars" REQUIRE "{}<>" DELIMITERS; DEFINE #="comment",thru={ step 1 until },crlf={('15)&('12)},ALT={'175&""},CR={('15)&""}; # REQUIRE "JOSLIB.REQ[LIB,JOS]" SOURCE!FILE; EXTERNAL PROCEDURE READ_COMMAND(STRING Prompt;REFERENCE STRING Cbits,Arg2,Arg1,Cmd); EXTERNAL PROCEDURE SUPCT; COMMENT Inhibit activation on \alpha-T,\alpha-L,\alpha-B - the SUPCT bit; EXTERNAL STRING PROCEDURE Cvbs(BOOLEAN B); EXTERNAL STRING PROCEDURE Cvfs(REAL r); # STRING Ffile,Ifile,Ofile; # INTEGER Nfft,Nspec,Nh,Nx,Nhop,Ndec; STRING Prompt; IF Nfft LEQ 0 THEN # the test is for saving defaults across <CALL> START; BEGIN "defaults" Nfft <- 1024; Nx <- 676; Nh <- 0; Nhop <- Nx/2; Ndec <- 1; WinType <- Hamming; Trace <- 0; DoFlt <- FALSE; DoSynth <- TRUE; SwapOut <- FALSE; InstantRise <- FALSE; END "defaults"; Idev <- Odev <- "UDP2"; Ifile <- "PC3R.SND[XF,JOS]"; Ffile <- "TEST.FLT"; Ofile <- DerivedName(Ifile,"S"); HaveIfile <- HaveFfile <- HaveOfile <- HavePack <- FALSE; WHILE TRUE DO BEGIN "OmniLoop" WHILE TRUE DO BEGIN "OuterParameters" STRING Bucky,Arg2, Arg1,Cmd; INTEGER Boolhak,Brk; COMMENT Enforce parameter consistency constraints; WinType <- (1 MAX WinType MIN Nwins); Nx <- Nx MAX 1; IF Nfft < (i <- 2**(1+(i <- LOG(Nfft)/LOG(2)))) THEN PRINT(" Transform size increased to next power of 2 = ",Nfft <- i,CrLf); IF Nh > Nfft THEN PRINT(" Transform size increased to ", Nfft <- 2**(1+(i <- LOG(Nh+Nx)/LOG(2))),CrLf); IF SwapOut THEN DoFlt <- DoSynth <- FALSE; IF SwapOut THEN BEGIN OutF(Pack) <- 3; HavePack <- TRUE END; IF DoFlt AND (Nh+Nx GEQ Nfft) THEN PRINT("*** FILTER WILL TIME ALIAS ***",CrLf, " (FFT size should be at least frame size plus filter length - 1.)",CrLf, " To avoid time aliasing, set FFT size to at least ",Nh+Nx-1,CrLf, " or reduce data frame size and/or filter length",CrLf); DoOut <- (DoFlt OR DoSynth OR SwapOut); IF NOT DoOut THEN PRINT(" Warning: No output signal will be generated",CrLf, "Only amplitude and frequency envelopes will be computed.",CrLf); IF NOT (DoFlt OR DoSynth) THEN Ndec <- 1; Prompt <- Crlf& "Window("&CVS(WinType)&"="&WinStr& ") TransformSize("&CVS(Nfft)& ") DataLength("&CVS(Nx)& ") HopSize("&CVS(Nhop)& ")"&CRLF&" "& (IF DoFlt THEN "LengthFilter("&CVS(Nh)&") " ELSE NULL)& "Input("&Idev&":"&Ifile& ") Output("&Odev&":"&Ofile& ") PackingOut("&CVS(OutF(Pack))& ") "&(IF DoFlt THEN "Filter("&Ffile&")" ELSE NULL)&CrLf&" "& (IF (DoFlt OR DoSynth) THEN "Compression("&CVS(Ndec)&") " ELSE NULL)& "AdditiveSynthesis("&CVBS(DoSynth)& ") UseFilter("&CVBS(DoFlt)& ") XchangeOut("&CVBS(SwapOut)& ") or ?:"; COMMENT General command is "arg2,arg1,cmd" or "arg2,arg1 \alpha-cmd" or "arg2,arg1 \beta-cmd" or "arg2,arg1 \alpha-\beta-cmd"; READ_COMMAND (Prompt,Bucky,Arg2,Arg1,Cmd); COMMENT Allow boolean B to be set TRUE with \alpha-B or B<return> or FALSE with \beta-B or <any arg>,B<return>; Boolhak <- INTSCAN(Bucky,0); IF Boolhak \leq 1 THEN Boolhak <- 0; CASE Cmd OF BEGIN "SetParameters" ["?"] HELP(IF Arg1 THEN Arg1[1 FOR 1] ELSE "TopLevel"); ["W"] WinType <- INTSCAN(Arg1,Brk); ["T"] Nfft <- INTSCAN(Arg1,Brk); ["D"] Nx <- INTSCAN(Arg1,Brk); ["H"] Nhop <- INTSCAN(Arg1,Brk); ["L"] Nh <- INTSCAN(Arg1,Brk); ["C"] Ndec <- INTSCAN(Arg1,Brk); ["A"] DoSynth <- NOT (Arg1 + Boolhak); ["U"] DoFlt <- NOT (Arg1 + Boolhak); ["X"] SwapOut <- NOT (Arg1 + Boolhak); ["Z"] Trace <- INTSCAN(Arg1,Brk); ["I"] IF (HaveIfile <- GetIfile(IF Arg1 NEQ NULL THEN Arg1 ELSE Ifile)) THEN BEGIN IF NOT HaveOfile THEN Ofile <- DerivedName(Ifile,"S"); IF NOT HavePack THEN BEGIN OutF(Pack) <- (IF SwapOut THEN 3 ELSE InF(Pack)); HavePack <- TRUE; END; END; ["O"] HaveOfile <- GetOfile(IF Arg1 NEQ NULL THEN Arg1 ELSE Ofile); ["P"] IF Arg1 NEQ NULL THEN OutF(Pack) <- INTSCAN(Arg1,0) ELSE BEGIN PRINT(CrLf,"Packing codes are (0=12b, 1=18b, 3=FP, 4=16b SAM, 5=20b SAM)",CrLf, "Output packing code:"); Arg1 <- INCHWL; IF !SKIP!=ALT THEN CONTINUE "OmniLoop"; OutF(Pack) <- (IF Arg1=NULL THEN Sam16 ELSE INTSCAN(Arg1,0)); PRINT("Packing code set to ",OutF(Pack),CrLf); HavePack <- TRUE; END; ["F"] BEGIN Ffile <- Arg1&".FLT"; IF NOT (HaveFfile <- GetFlt(Ni,No,Ic,Oc,Ffile,FALSE,FALSE)) THEN CONTINUE "OmniLoop"; IF No>1 THEN PRINT(" Recursive part of filter ignored.",CRLF); Nh <- Ni; END; [";"] ; COMMENT For comments in command lines; [ALT] ["E"] CALL(0,"EXIT"); [CR] DONE "OuterParameters"; ELSE PRINT(" what?",Crlf) END "SetParameters"; END "OuterParameters"; IF NOT (HaveIfile OR (HaveIfile <- GetIfile(Ifile))) THEN CALL(0,"EXIT"); IF NOT HaveOfile THEN Ofile <- DerivedName(Ifile,"S"); IF NOT HavePack THEN BEGIN OutF(Pack) <- (IF SwapOut THEN 3 ELSE InF(Pack)); HavePack <- TRUE; END; IF InF(#chans)>1 THEN BEGIN PRINT(Crlf,"Sorry, can only do 1-channel files."); HaveIfile <- FALSE; CONTINUE "OmniLoop"; END; IF NOT (HaveOfile OR NOT DoOut OR (HaveOfile <- GetOfile(Ofile))) THEN CALL(0,"EXIT"); IF DoFlt AND NOT HaveFfile THEN DO BEGIN IF NOT (HaveFfile <- GetFlt(Ni,No,Ic,Oc,Ffile,FALSE,FALSE)) THEN CALL(0,"EXIT"); IF No>1 THEN PRINT(" Recursive part of filter ignored.",CRLF); Nh <- Ni; END UNTIL HaveFfile; Nframes <- (InF(#samps)-Nx)/Nhop + 1; # Number of frames to process; TmpStr <- "PARSHL: Input file was "&Idev&":"&Ifile&CrLf&Tab& (IF DoFlt THEN "Filter="&Ffile&CrLf&Tab ELSE NULL)&" "& (IF DoSynth THEN " AS" ELSE NULL)& " Nframes="&CVS(Nframes)& " Nfft="&CVS(Nfft)& " Window="&WinStr& " Nframe="&CVS(Nx)& " Nhop="&CVS(Nhop)& " Compression="&CVS(Ndec)&CrLf&Tab& "NOT FINISHED"&CrLf& "(+)"&Tab&InF(Text)&Crlf; IF DoOut THEN BEGIN "SUOutSound" OutH[0] <- 0; OutF(Dev ) <- ODev; OutF(Name ) <- Ofile; OutF(Clock ) <- InF(Clock)/Ndec; OutF(#chans) <- InF(#chans); OutF(#ticks) <- InF(#ticks)*Ndec; OutF(#samps) <- 0; OutF(Text ) <- TmpStr; WriteH(Head,OutF(Clock),OutF(Pack),OutF(#chans),OutF(#ticks),0,OutF(Text)); USETO(OutF(Channel),1); ARRYOUT(OutF(Channel),Head[1],128); END "SUOutSound"; BEGIN "SUAmps" DO BEGIN "GAF" Tstr <- DerivedName((IF HaveOfile THEN Odev ELSE Idev)&":"& (IF HaveOfile THEN Ofile ELSE Ifile),"A"); FNparse(Tstr,AmpDev <- NULL,AmpFile); PRINT(CrLf,"Output amplitude envelopes file (=",AmpDev,":",AmpFile,"): "); Tstr <- INCHWL; IF !SKIP!=ALT THEN CALL(0,"EXIT"); FNparse(Tstr,AmpDev,AmpFile); PRINT(Tab,"Writing file ",AmpDev,":",AmpFile,Crlf); OPEN(AmpF(Channel) <- GETCHAN,AmpDev,'17,0,0,200,Brk,Eof); ENTER(AmpF(Channel),AmpFile,FAIL); IF FAIL THEN PRINT("Can't ENTER amplitudes output file",CrLf); END "GAF" UNTIL NOT FAIL; AmpH[0] <- 0; AmpF(Dev ) <- AmpDev; AmpF(Name ) <- AmpFile; AmpF(Clock ) <- InF(Clock)/Ndec; AmpF(#chans) <- InF(#chans); AmpF(#ticks) <- InF(#ticks)*Ndec; AmpF(#samps) <- 0; AmpF(Pack ) <- 3; AmpF(Text ) <- TmpStr; WriteH(Head,AmpF(Clock),AmpF(Pack),AmpF(#chans),AmpF(#ticks),0,AmpF(Text)); # Block size parameter (not yet supported by WriteH); Head[8] <- MEMORY[LOCATION(Nframes),REAL]; USETO(AmpF(Channel),1); ARRYOUT(AmpF(Channel),Head[1],128); END "SUAmps"; BEGIN "SUFrqs" DO BEGIN "GFF" EXTERNAL STRING PROCEDURE NAME(STRING Name); COMMENT Return NAME part of filename; EXTERNAL STRING PROCEDURE EXT(STRING Name); COMMENT Return extension part of filename; EXTERNAL STRING PROCEDURE PPN(STRING Name); COMMENT Return PPN part of filename; Tstr <- Name(AmpFile); Tstr <- Tstr[1 TO LENGTH(Tstr)-1]; # Strip off trailing "A"; Tstr <- Tstr&Ext(AmpFile)&Ppn(AmpFile); Tstr <- DerivedName(AmpDev&":"&Tstr,"F"); FNparse(Tstr,FrqDev <- NULL,FrqFile); PRINT(CrLf,"Output frequency envelopes file (=",FrqDev,":",FrqFile,"): "); Tstr <- INCHWL; IF !SKIP!=ALT THEN CALL(0,"EXIT"); FNparse(Tstr,FrqDev,FrqFile); PRINT(Tab,"Writing file ",FrqDev,":",FrqFile,Crlf); OPEN(FrqF(Channel) <- GETCHAN,FrqDev,'17,0,0,200,Brk,Eof); ENTER(FrqF(Channel),FrqFile,FAIL); IF FAIL THEN PRINT("Can't ENTER Frq output file",CrLf) END "GFF" UNTIL NOT FAIL; FrqH[0] <- 0; FrqF(Dev ) <- FrqDev; FrqF(Name ) <- FrqFile; FrqF(Clock ) <- InF(Clock)/Ndec; FrqF(#chans) <- InF(#chans); FrqF(#ticks) <- InF(#ticks)*Ndec; FrqF(Pack ) <- 3; FrqF(#samps) <- 0; FrqF(Text ) <- TmpStr; WriteH(Head,FrqF(Clock),FrqF(Pack),FrqF(#chans),FrqF(#ticks),0,FrqF(Text)); # Block size parameter (not yet supported by WriteH); Head[8] <- MEMORY[LOCATION(Nframes),REAL]; USETO(FrqF(Channel),1); ARRYOUT(FrqF(Channel),Head[1],128); END "SUFrqs"; CALL (InF(Channel), "SHOWIT"); # Simulate an <esc>2x for the input channel; SETFORMAT(0,5); # For buffer begin-time print-out and squelched frqs; Nspec <- (Nfft DIV 2) + 1; Maxamp <- 0; Nhops <- 0; # Counts up to Nframes unless aborted with ESC-I; # changed from 2 to 4, XJS 3.12.87; SigScl <- 4/Nx; # Guess for Hamming window, 50% overlap; REQUIRE CrLf&" IS SIGSCL CORRECT?? (Synth scaling)"&CrLf MESSAGE; COMMENT Additional input parameters for PARSHL analysis; IF MaxLins LEQ 0 THEN BEGIN "Idefaults" MinSep <- InF(Clock)/(Nx/4); # This is right when there are 4 period per frame; # Each valid peak should be (Nfft/Nx)*4 bins wide (4 for Hamming); MinWid <- 2.0*Nfft/Nx+1; # Half of expected width plus 1 (side-lobes rejected); MaxLins <- 60 MIN 0.5*InF(Clock)/MinSep; MaxOscs <- 40 MIN 0.5*InF(Clock)/MinSep; Fc1 <- InF(Clock)/1000; Fc2 <- InF(Clock)/2; Thresh <- -30; Hyst <- 0.1; # DAmax <- 10; # Disabled; DFmax1 <- MinSep/2; DFmax2 <- DFmax1; END "Idefaults"; WHILE TRUE DO BEGIN "InnerParameters" STRING Bucky,Arg2, Arg1,Cmd; INTEGER Boolhak,Brk; MinSep <- (0 MAX MinSep MIN InF(Clock)/4); MinWid <- (0 MAX MinWid MIN Nspec); MaxLins <- (1 MAX MaxLins MIN Nspec); MaxOscs <- (1 MAX MaxOscs MIN MaxLins); Thresh <- (-760 MAX Thresh MIN 760); Hyst <- (Hyst MAX 0); DFmax1 <- (0 MAX DFmax1 MIN InF(Clock)/2); DFmax2 <- (0 MAX DFmax2 MIN InF(Clock)/2); Prompt <- Crlf& "MinSpacing("&Cvfs(MinSep)&"Hz"& ") BinMin("&CVS(MinWid)& ") Nlines("&CVS(MaxLins)& ") Oscs("&CVS(MaxOscs)& ") InstantRise("&Cvbs(InstantRise)&")"&CRLF& " FirstFrq("&Cvfs(Fc1)& ") LastFrq("&Cvfs(Fc2)& ") Thresh("&Cvfs(Thresh)&"dB"&")"&CRLF& " Hyst("&Cvfs(Hyst)&"dB"& ") DFmax("&Cvfs(DFmax1)&"Hz"& ") UltDFmax("&Cvfs(DFmax2)&"Hz"& ") or ?:"; READ_COMMAND (Prompt,Bucky,Arg2,Arg1,Cmd); Boolhak <- INTSCAN(Bucky,0); IF Boolhak \leq 1 THEN Boolhak <- 0; CASE Cmd OF BEGIN "SetParameters" ["?"] HELP(IF Arg1 THEN Arg1[1 FOR 1] ELSE "SubLevel"); ["M"] MinSep <- REALSCAN(Arg1,Brk) MAX 0.0; ["N"] MaxLins <- INTSCAN(Arg1,Brk) MAX 1; ["O"] MaxOscs <- INTSCAN(Arg1,Brk) MAX 1; ["F"] Fc1 <- REALSCAN(Arg1,Brk) MAX 0.0; ["L"] Fc2 <- REALSCAN(Arg1,Brk) MIN InF(Clock)/2; ["T"] Thresh <- REALSCAN(Arg1,Brk); ["I"] InstantRise <- NOT (Arg1 + Boolhak); ["H"] Hyst <- REALSCAN(Arg1,Brk) MAX 0.0; ["D"] DFmax1 <- DFmax2 <- (REALSCAN(Arg1,Brk) MAX 0.0); ["U"] DFmax2 <- REALSCAN(Arg1,Brk) MAX 0.0; ["B"] MinWid <- INTSCAN(Arg1,Brk) MAX 0; ["Z"] Trace <- INTSCAN(Arg1,Brk); [";"] ; COMMENT For comments in command lines; [ALT] ["E"] CONTINUE "OmniLoop"; [CR] DONE "InnerParameters"; ELSE PRINT(" hmmm?",Crlf) END "SetParameters"; END "InnerParameters"; DONE "OmniLoop"; END "OmniLoop"; END "GetPars"; COMMENT Allocation of analysis data structures; BEGIN "ALAR" # Allocate arrays; # REQUIRE "SIGLIB.REL[SUB,SYS]" LIBRARY; EXTERNAL PROCEDURE !FFA(REAL ARRAY B; REFERENCE INTEGER NFFT); EXTERNAL PROCEDURE !FFS(REAL ARRAY B; REFERENCE INTEGER NFFT); INTEGER Yp,Xp,Bp,Nout,i; REAL ARRAY X[1:Nfft+2],H[1:Nfft+2],XmagDB[1:Nspec], OutBuf[1:2*Nfft],WinBuf[1:Nx]; REAL ARRAY Amps,Frqs[1:MaxLins,1:Nframes]; # Output database; INTEGER ARRAY Nactive[1:Nframes]; # No. active lines each frame; # Data structures for additive synthesis oscillators. (Use explained next page); INTEGER CurOsc,CurLin,Nlins,Noscs,PrvNoscs; INTEGER ARRAY OscOfLin[1:MaxLins]; # Osc no. assigned to each Lin; INTEGER ARRAY PrvLinOfOsc[1:MaxOscs]; # Lin no. assigned to each osc; INTEGER ARRAY LinOfOsc[1:MaxOscs]; # PrvLinOfOsc for next frame; INTEGER ARRAY OscPhs[1:MaxOscs]; # Current phases (sum of frequency); REAL ARRAY PrvOscAmp[1:MaxOscs]; # Current amplitudes (Linar ramps to targets); REAL ARRAY PrvOscFrq[1:MaxOscs]; # Current frequency (Linar ramp to that of Lin); REAL ARRAY OscAmp[1:MaxOscs]; # Target amplitude; REAL ARRAY OscFrq[1:MaxOscs]; # Target frequency; REAL ARRAY LinAmpDB[1:MaxLins]; # Target amplitudes of some osc in dB; REAL ARRAY LinAmp[1:MaxLins]; # Target amplitudes of some osc; REAL ARRAY LinFrq[1:MaxLins]; # Current instantaneous frequency; # REAL ARRAY LinPhs[1:MaxLins]; # Phase is the first thing thrown away; COMMENT Oscillator allocation utilities; DEFINE UDTrace = " (ABS(Trace)>2) "; DEFINE PrvOscOn(x) = { (PrvLinOfOsc[x] > 0) }, PrvOscFree(x) = { (PrvLinOfOsc[x] = 0) }, PrvOscSquelched(x) = { (PrvLinOfOsc[x] < 0) }, OscOn(x) = { (LinOfOsc[x] > 0) }, OscFree(x) = { (LinOfOsc[x] = 0) }, OscSquelched(x) = { (LinOfOsc[x] < 0) }, StopOsc(x) = { BEGIN LinOfOsc[x] <- -ABS(PrvLinOfOsc[x]); IF UDtrace THEN PRINT (" Osc ",x," turned off.",CrLf) END }, LinFree(x) = { (OscOfLin[x] = 0) }, LinClaimed(x) = { (OscOfLin[x] > 0) }; INTEGER PROCEDURE NxtPrvOscOn(INTEGER CurOsc); COMMENT Return next active oscillator after CurOsc, with wrap-around. Return 0 if no active oscillators; BEGIN "NxtPrvOscOn" INTEGER cnt,Found; Found <- 0; FOR cnt <- 1 Thru MaxOscs DO BEGIN CurOsc <- CurOsc+1; IF CurOsc>MaxOscs THEN CurOsc <- CurOsc-MaxOscs; IF PrvOscOn(CurOsc) THEN BEGIN Found <- CurOsc; DONE END; IF UDtrace THEN PRINT (" Skipping inactive Prv Osc number ",CurOsc,CrLf); END; IF UDtrace THEN PRINT (" Next active Prv Osc is number ",CurOsc,CrLf); IF Found=0 THEN PRINT(CrLf,"*!*!* Next active Prv Osc not found!",CrLf); RETURN(Found) END "NxtPrvOscOn"; INTEGER PROCEDURE NxtOscOn(INTEGER CurOsc); COMMENT Return next active oscillator after CurOsc, with wrap-around. Return 0 if no active oscillators; BEGIN "NxtOscOn" INTEGER cnt,Found; Found <- 0; FOR cnt <- 1 Thru MaxOscs DO BEGIN CurOsc <- CurOsc+1; IF CurOsc>MaxOscs THEN CurOsc <- CurOsc-MaxOscs; IF OscOn(CurOsc) THEN BEGIN Found <- CurOsc; DONE END; IF UDtrace THEN PRINT (" Skipping inactive Osc number ",CurOsc,CrLf); END; IF UDtrace THEN PRINT (" Next active Osc is number ",CurOsc,CrLf); IF Found=0 THEN PRINT(CrLf,"*!*!* Next active osc not found!",CrLf); RETURN(Found) END "NxtOscOn"; INTEGER PROCEDURE NxtOscFree(INTEGER CurOsc); COMMENT Return next free oscillator after CurOsc, with wrap-around. Return 0 if no free oscillators; BEGIN "NxtOscFree" INTEGER cnt,Found; Found <- 0; FOR cnt <- 1 Thru MaxOscs DO BEGIN CurOsc <- CurOsc+1; IF CurOsc>MaxOscs THEN CurOsc <- CurOsc-MaxOscs; IF OscFree(CurOsc) THEN BEGIN Found <- CurOsc; DONE END; IF UDtrace THEN PRINT (" Skipping non-free Osc number ",CurOsc,CrLf); END; IF UDtrace THEN PRINT (" Next free Osc is number ",CurOsc,CrLf); IF Found=0 THEN PRINT(CrLf,"*!*!* Next free osc not found!",CrLf); RETURN(Found) END "NxtOscFree"; INTEGER PROCEDURE NxtOscEnding(INTEGER CurOsc); COMMENT Return next Ending oscillator after CurOsc, with wrap-around. Return 0 if no Ending oscillators; BEGIN "NxtOscEnding" INTEGER cnt,Found; Found <- 0; FOR cnt <- 1 Thru MaxOscs DO BEGIN CurOsc <- CurOsc+1; IF CurOsc>MaxOscs THEN CurOsc <- CurOsc-MaxOscs; IF OscSquelched(CurOsc) THEN BEGIN Found <- CurOsc; DONE END; IF UDtrace THEN PRINT (" Skipping non-Ending Osc number ",CurOsc,CrLf); END; IF UDtrace THEN PRINT (" Next Ending Osc is number ",CurOsc,CrLf); IF Found=0 THEN PRINT(CrLf,"*!*!* Next Ending osc not found!",CrLf); RETURN(Found) END "NxtOscEnding"; INTEGER PROCEDURE ClosestOscFree(REAL NewFrq); COMMENT Return free oscillator with frequency closest to NewFrq. Return 0 if no free oscillators; BEGIN "ClosestOscFree" INTEGER Cnt,Found; REAL Dis,BestDis; Found <- NxtOscFree(0); IF Found=0 THEN BEGIN PRINT(CrLf,"*!*!* Next free osc not found!",CrLf); RETURN(Found) END; BestDis <- 1.0@38; Found <- 0; FOR cnt <- 1 Thru MaxOscs DO BEGIN IF OscFree(Cnt) THEN IF LinOfOsc[Cnt] NEQ 0 THEN IF (Dis <- ABS(NewFrq-LinFrq[ABS(LinOfOsc[Cnt])]))<BestDis THEN BEGIN Found <- Cnt; BestDis <- Dis; END; END; IF Found=0 THEN Found <- NxtOscFree(0) # None were ever used before; ELSE IF UDtrace THEN BEGIN PRINT (" Desired frq = ",NewFrq,CrLf); PRINT (" Closest frq = ",LinFrq[ABS(LinOfOsc[Found])],CrLf); PRINT (" Closest free osc is number ",Found,CrLf); END; RETURN(Found) END "ClosestOscFree"; COMMENT CkFrqs is OBSOLETE (replaced by GetClosestFrq); INTEGER PROCEDURE CkFrqs(INTEGER CurOsc; REAL DFlim); # Search for a line within specs, starting from where last one was. We assume partials are always quick-sorted by frequency so that usually the answer is a next-door neighbor ; BEGIN "CkFrqs" INTEGER LstLin; REAL TF,PF,DF,t; CurOsc <- NxtPrvOscOn(CurOsc); IF CurOsc LEQ 0 THEN RETURN(CurOsc); PF <- OscFrq[CurOsc]; # Former target frequency of oscillator CurOsc; LstLin <- PrvLinOfOsc[CurOsc] MIN Nlins; # Line this osc had last frame; IF LstLin<1 THEN BEGIN PRINT(" *** Nlins=0? ***"); RETURN(CurOsc) END; TF <- LinFrq[LstLin]; # Target frequency using last frame assignment; DF <- ABS(TF-PF); # Absolute change in frequency; IF UDtrace THEN PRINT( " Prv Frq for Osc ",CurOsc," was Line ",LstLin,"=",PF,CrLf, " Trg Frq for Osc ",CurOsc," on same Line ",LstLin,"=",TF,CrLf, " Del Frq for Osc ",CurOsc," would then be ",100*DF,"%",CrLf); IF DF > DFlim THEN BEGIN "DFerror" INTEGER Found; IF UDtrace THEN PRINT( "$$$ Frequency tolerance exceeded for Osc ",CurOsc," Frame ",Frame,CrLf); Found <- 0; DEFINE FrqInRange = { ABS(LinFrq[CurLin]-PF) LEQ DFlim }; DEFINE GotIt = { BEGIN Found <- CurLin; IF Trace THEN PRINT(" Found = ",Found,CrLf); DONE END }; FOR CurLin <- LstLin-1 STEP -1 UNTIL 1 DO IF FrqInRange THEN Gotit; IF Found=0 THEN FOR CurLin <- LstLin+1 STEP 1 UNTIL Nlins DO IF FrqInRange THEN Gotit; IF Found=0 THEN BEGIN "LineLost" PRINT(" LINE AT ",PF,"Hz LOST!",CrLf); StopOsc(CurOsc); END "LineLost" ELSE IF OscOfLin[Found] NEQ 0 THEN BEGIN "ohno" # Serious problem. The fix is to go find the other nearby line; PRINT("*!*!* LINE ",Found, " HAS CAPTURED OSCILLATORS ",OscOfLin[Found]," AND ",CurOsc,CrLf, " I HAVE TO DELETE ONE OSCILLATOR AND PROBABLY LOSE A NEARBY LINE",CrLf); StopOsc(CurOsc); END "ohno" ELSE BEGIN "LineFound" LinOfOsc[CurOsc] <- Found; OscOfLin[Found] <- CurOsc; Noscs <- Noscs+1; IF UDtrace THEN PRINT( " *New* line number is ",LinOfOsc[CurOsc], "=",LinFrq[LinOfOsc[CurOsc]], " hopefully closer to PF=",PF,CrLf) END "LineFound" END "DFerror" ELSE BEGIN "DFok" LinOfOsc[CurOsc] <- LstLin; OscOfLin[LstLin] <- CurOsc; Noscs <- Noscs+1; IF UDtrace THEN PRINT(" # SAME # line number used for osc ",CurOsc,CrLf) END "DFok"; RETURN(CurOsc); END "CkFrqs"; RECURSIVE PROCEDURE GetClosestFrq(INTEGER CurOsc; REAL DFmax); # Go through all active lines and find the one closest (BestFrq) to the previous frequency (PF) of oscillator CurOsc. If the difference between BestFrq and PF exceeds the frequency change limit (DFmax), the oscillator is turned off. (If it is already off it stays off.) On the other hand, if ABS(BestFrq-PF)<DFmax, a check is made to see if any other running osc has claimed this line already. If so, it is determined who is closer, and the loser is turned off. If the DFmax test passes and there are no collisions, the line is claimed by placing its number in LinOfOsc[CurOsc]. The osc is then running because LinOfOsc[CurOsc] will then be positive. ; BEGIN "GetClosestFrq" INTEGER j,BestLin,CurLin; REAL PF,CurDist,MinDist,BestFrq; # IF NOT PrvOscOn(CurOsc) THEN PRINT(" *** GetClosestFrq: Called on squelched osc ",CurOsc," ***",CrLf); PF <- OscFrq[CurOsc]; # Former target frequency of oscillator CurOsc; IF UDtrace THEN PRINT(" Prv frq for osc ",CurOsc," = ",PF,CrLf); BestLin <- 0; MinDist <- 1.0@38; DEFINE Dist(x,y) = { ABS((x)-(y)) }; FOR CurLin <- 1 STEP 1 UNTIL Nlins DO IF MinDist>(CurDist <- Dist(PF,LinFrq[CurLin])) THEN IF LinFree(CurLin) THEN BEGIN "PotentiallyMine" MinDist <- CurDist; BestLin <- CurLin END "PotentiallyMine" ELSE BEGIN "PotentiallyHis" INTEGER OtherOsc; REAL CurFrq; CurFrq <- LinFrq[CurLin]; OtherOsc <- OscOfLin[CurLin]; # Osc who has already claimed this line; IF CurDist<Dist(CurFrq,OscFrq[OtherOsc]) THEN BEGIN "HeCantHaveIt" MinDist <- CurDist; BestLin <- CurLin; IF UDtrace THEN PRINT(" GetClosestFrq Recursing on bumped osc ",OtherOsc,CrLf); OscOfLin[CurLin] <- CurOsc; # Tentatively claim this while other guy fishes; GetClosestFrq(OtherOsc,DFmax); # Go fish, OtherOsc; OscOfLin[CurLin] <- 0; # Unclaim; END "HeCantHaveIt" END "PotentiallyHis"; IF BestLin LEQ 0 THEN BEGIN "SureIsCrowded" PRINT(" *!*!* Osc ",CurOsc," could find no best line!!",CrLf); StopOsc(CurOsc); RETURN END "SureIsCrowded"; # Now BestLin points to the best line for osc CurOsc with all contention resolved; BestFrq <- LinFrq[BestLin]; IF UDtrace THEN PRINT(" Bst frq for osc ",CurOsc," = ",BestFrq,CrLf); IF MinDist > DFmax THEN BEGIN "DFerror" # And after all that!; IF UDtrace THEN PRINT("$$$ Frequency tolerance exceeded for Osc ",CurOsc,CrLf); StopOsc(CurOsc); # If already stopped, StopOsc is a noop; END "DFerror" ELSE BEGIN "TakeIt" LinOfOsc[CurOsc] <- BestLin; OscOfLin[BestLin] <- CurOsc; IF UDtrace THEN PRINT(" Osc ",CurOsc," grabs line ",BestLin,CrLf); END "TakeIt"; RETURN; END "GetClosestFrq"; COMMENT UpdateMap - Assign oscillators target values to partials. UpdateMap figures out which spectral lines go with which running oscillators. It makes extensive reference to the data structure of the previous page. (The routine is declared here to avoid a long argument list.) FindPartials prepares a list of partial amplitudes and frequencies active in the current frame. Since the partials (or lines) are found in order of decreasing amplitude, they can get arbitrarily reordered from frame to frame. It helps to sort by frequency the partials. However, there is still the problem of partials appearing and disappearing. This version of UpdateMap assumes lines to be sorted by ascending frequency. Here is a strategy: Initialization is trivial, so assume we are into the analysis at time Frame. Suppose there are Noscs active oscillators. Then (1) Each active oscillator looks for its line by finding the one which is closest in frequency. If it cannot find its line then it assumes the line disappeared and puts itself into the ramp-off state. (The previous amplitude tells whether this is a reasonable assumption, but the information is not being put to use here.) When an oscillator finds its line, it marks the line as taken. This prevents crossing partials from putting two oscillators on the same line and losing the other one. Thus, an oscillator must find its line among those not already taken. A count is made of the total number of line-to-osc assignments. There cannot be more successfully assigned oscs than than lines because of the "taken" mark interlock. However, there can be lines left over after all bands have been searched. (2) If there are one or more new lines, a pass is made through the Lines-in-Use array, and an oscillator is dispatched onto each line found not to be taken. An oscillator marks a line as taken by storing its id in an array. Therefore, if a collision occurs, the oscillator on the closest track can be given the line. In the current implementation, only a warning is issued. Each oscillator has 3 states: On, off, stopping. On means that the oscillator is to ramp from its previous amplitude to the current amplitude over Nhop samples. Off means no output. Stopping means the oscillator is ramping to zero. If we can ramp to zero from any amplitude in Nhop samples, we only need On and Off states (Stopping is then equivalent to Off with a previous amplitude > 0). However, it is also possible that ramps should comprise several hops when going from an arbitrary amplitude to 0. A hop is typically on the order of two periods of sound. JOS 14-JUN-85 : After getting the above working, I think the osc-to-line assignment strategy should be changed so that an oscillator is assigned a fixed frequency band. That way, an oscillator will not jump from line to line as we see now. This wastes oscillators (because bands with no lines are generating zeros) but consolidation can take place later. For now, I think it is best to have convenient AMPS and FRQS functions which are easy to look at. When an oscillator loses its line and gets dispatched on another line far away in frequency, it makes the AMPS and FRQS arrays unintelligible. Thus, UpDateMap is based on these changes. DAJ mentions what if a line is crossing back and forth between two bands? Instead, how about doing the previous version, but when assigning free oscs to new lines, find the osc with closest previous frequency. A losing case here is when a new line appears close to (but below) another line and captures the other lines osc. JOS 15-JUN-85 : After talking with Gerold, it was decided that we will do the following allocation strategy: * The input sound is reversed in time to allow postponement of the attack analysis until the end. * Working backwards through the sound, we dispatch a new oscillator on each new sinusoidal line which appears. Once committed to a frequency, an oscillator cannot be reassigned to a new frequency except by tracking valid glissandos. * For each frame, each oscillator finds the line which is closest to its current frequency. The current frequency is normally the frequency of the line in the previous frame used by this oscillator, except when the oscillator is off. A stopped osc remembers its last valid frequency as its current frequency. The difference between the closest line frequency and the current frequency are compared to a maximum-change limit. If this limit is exceeded the oscillator is turned off (or left off). Otherwise, a check is made to see if the best line has been claimed by another oscillator already in the current frame. If not, the osc claims the line and we go process the next osc. If there is a collision, we give the line to the osc which has to move the shortest distance in frequency to reach the new line. The osc which does not get the new line (in a collision) is turned off and its "current frequency" is rolled back to what it was before it claimed the new line. *** NOTE *** This is not optimal. It may be that OSC 1 claims LINE K+1 instead of LINE K which it normally claims. OSC 2 comes along and takes back LINE K. OSC 1 is turned off, and nobody can claim LINE K which is still there. Ideally, if an OSC is bumped from a line it claimed because another OSC came along later with a better fit to it, the bumped osc should get another pass to look for a "consolation line". [JOS: Implemented 15-JUN-85 9:21] REMARK: When the frequency deviation exceeds the allowed level, it is normally because the line for that oscillator dropped out. However, we can also get shaken loose by excessive frequency vibrato. In this case one oscillator turns off and another will hopefully start up elsewhere. 8-JUL-85 Consider allowing Oscs to find their peaks in DBspec instead of LinFrqs. Operation would be exactly as now, except the raw DB mag spectrum is searched for a local max nearest the current osc frq. Marking of a peak as "taken" is as before but now using the FindPeak method of peak removal. Every osc must be allowed to search the raw initial spectrum. GRS has suggested doing groups reduction on the mag^2 spectrum (summing power within a group and letting center frq of the group stand for line frq for the group). This way, PARSHL runs as if there were only 16 or so lines in the spectrum. Each group becomes a "virtual line" with its own AMP and FRQ. ; COMMENT (UpdateMap) - Initialization; PROCEDURE UpdateMap; COMMENT Arguments (See "Allocation of analysis data structures" above); BEGIN "UpdateMap" INTEGER i,Nadd,Owid,Odig; STRING CrLfd; REAL PROCEDURE DFmax(INTEGER CurOsc); # Return maximum allowed glissando for oscillator CurOsc; BEGIN "DFmax" OWN BOOLEAN ARRAY Inited[1:1]; # Array so <CALL>START<CR> will clear it; OWN REAL Alpha, Beta, DFmaxr; IF NOT Inited[1] THEN BEGIN "DFinit" REAL f1,f2; INTEGER kase; Inited[1] <- TRUE; f1 <- Fc1 MAX 0; f2 <- Fc2 MIN Fs/2; IF DFmax1=DFmax2 THEN kase <- 3 ELSE IF f1=0 THEN kase <- 2 ELSE kase <- 1; Alpha <- (CASE kase OF (0,(DFmax2/f2-DFmax1/f1)/(f2-f1),(DFmax2-DFmax1)/(f2-f1),0)); Beta <- (CASE kase OF (0,(DFmax1*f2/f1-DFmax2*f1/f2)/(f2-f1),(DFmax1*f2-DFmax2*f1)/(f2-f1),DFmax1)); END "DFinit"; DFmaxr <- Alpha*OscFrq[CurOsc]+Beta; IF Debug3 THEN PRINT(" Computed DFmax for OSC ",CurOsc," at freq ",OscFrq[CurOsc]," is ",DFmaxr,CrLf); RETURN(DFmaxr); END "DFmax"; GETFORMAT(Owid,Odig); IF Frame LEQ 1 THEN BEGIN "initialize" Noscs <- Nactive[Frame] MIN MaxOscs; Nlins <- Nactive[Frame] MIN MaxLins; FOR CurOsc <- 1 STEP 1 UNTIL Noscs DO BEGIN LinOfOsc[CurOsc] <- (CurLin <- CurOsc); PrvLinOfOsc[CurOsc] <- LinOfOsc[CurOsc]; # For next entry; OscOfLin[CurLin] <- CurOsc; OscPhs[CurOsc] <- 0; OscAmp[CurOsc] <- LinAmp[CurLin]; PrvOscAmp[CurOsc] <- (IF InstantRise THEN LinAmp[CurLin] ELSE 0); PrvOscFrq[CurOsc] <- LinFrq[CurLin]; OscFrq[CurOsc] <- LinFrq[CurLin]; END; PRINT(" Initialization of ",Noscs," oscillators to the tallest of ",Nlins," lines.",CrLf); RETURN END "initialize"; SETFORMAT(0,7); COMMENT (UpdateMap) - Association of spectral lines to oscs; Nlins <- Nactive[Frame]; # Number of Lins currently active; REQUIRE " PrvLinOfOsc only used for trace messages?" MESSAGE; ARRTRAN(PrvLinOfOsc,LinOfOsc); ARRCLR(LinOfOsc); ARRCLR(OscOfLin); IF UDtrace THEN BEGIN PRINT(CrLf,"------- UpdateMap entry on frame ",Frame," --------", CrLf, " Number of lines = ",Nlins," ... Number of oscs = ",Noscs,CrLf, " PrvLinOfOsc follows:",CrLf); FOR i <- 1 Thru MaxOscs DO PRINT(" ",PrvLinOfOsc[i]); END; FOR CurOsc <- 1 STEP 1 UNTIL Noscs DO GetClosestFrq(CurOsc,DFmax(CurOsc)); # Allocate oscillators to new lines, if any; Nadd <- (Nlins MIN MaxOscs)-Noscs; IF Nadd>0 THEN BEGIN "Add" PRINT("$$$ Adding ",Nadd," oscillator(s) $$$",CrLf); CurLin <- 0; FOR CurOsc <- Noscs+1 Thru Noscs+Nadd DO BEGIN "AddOsc" DO CurLin <- CurLin+1 UNTIL OscOfLin[CurLin]=0; ; # Find lin with no osc; OscOfLin[CurLin] <- CurOsc; LinOfOsc[CurOsc] <- CurLin; IF UDtrace THEN PRINT(" Osc ",CurOsc," dispatched to ",LinFrq[CurLin]," Hz",CrLf); END "AddOsc"; Noscs <- Noscs+Nadd; END "Add"; IF UDtrace THEN BEGIN PRINT(CrLf," <- *^Y <- *^YUpdateMap exit on frame ",Frame,CrLf, " PrvLinOfOsc follows:",CrLf); FOR CurOsc <- 1 Thru MaxOscs DO PRINT(" ",PrvLinOfOsc[CurOsc]); PRINT(CrLf," LinOfOsc follows:",CrLf); FOR CurOsc <- 1 Thru MaxOscs DO PRINT(" ",LinOfOsc[CurOsc]); PRINT(CrLf," OscOfLin follows:",CrLf); FOR CurLin <- 1 Thru MaxOscs DO PRINT(" ",OscOfLin[CurLin]); END; COMMENT (UpdateMap) - Update new amp/frq target; # Update target values for synthesis up to latest spectral frame; FOR CurOsc <- 1 Thru MaxOscs DO BEGIN "OutAF" PrvOscFrq[CurOsc] <- OscFrq[CurOsc]; IF OscOn(CurOsc) THEN OscFrq[CurOsc] <- LinFrq[LinOfOsc[CurOsc]]; PrvOscAmp[CurOsc] <- OscAmp[CurOsc]; OscAmp[CurOsc] <- (IF OscOn(CurOsc) THEN LinAmp[LinOfOsc[CurOsc]] ELSE 0); IF PrvOscAmp[CurOsc]=0 THEN PrvOscFrq[CurOsc] <- OscFrq[CurOsc]; END "OutAF"; CrLfd <- FALSE; DEFINE CkCrLf={ (IF NOT CrLfd THEN CrLf ELSE NULL) }; # Gad, what an awkward thing; FOR CurOsc <- 1 STEP 1 UNTIL Noscs DO BEGIN IF PrvOscFree(CurOsc) AND OscOn(CurOsc) THEN PRINT(CkCrLf," $$$ Osc ",CurOsc," *starting* on frequency ",OscFrq[CurOsc]," $$$",Crlfd <- CrLf); IF PrvOscSquelched(CurOsc) AND OscOn(CurOsc) THEN PRINT(CkCrLf," $$$ Osc ",CurOsc," *revived* on frequency ",OscFrq[CurOsc]," $$$",CrLfd <- CrLf); IF OscSquelched(CurOsc) AND PrvOscOn(CurOsc) THEN PRINT(CkCrLf," $$$ Osc ",CurOsc," *squelched* on frequency ",OscFrq[CurOsc]," $$$",CrLfd <- CrLf); END; SETFORMAT(Owid,Odig); END "UpdateMap"; COMMENT Synthesize - Use database to run oscillators up to latest targets; DEFINE UseFixedPoint = "FALSE"; # Set true for fast execution; DEFINE SinSiz = "512"; # No. wds in Sine table for synthesis; IFC UseFixedPoint THENC INTEGER ELSEC REAL ENDC ARRAY SinBuf[0:SinSiz-1]; # Sine table; REAL Mag; # Mag * Frq = Sine table increment; PROCEDURE Synthesize(INTEGER Nhop,Bp,Fs,Frame); # Crank out MaxOscs sinusoids from amplitude PrvOscAmp[i] to OscAmp[i], and frequency PrvOscFrq[i] to OscFrq[i] (integrating OscPhs[i]). Add result to OutBuf[Bp+1:Bp+Nhop]. Only Noscs oscs will be active, but there are also some Ending ones which have to be ramped to 0. Hence a loop from 1 to MaxOscs is required. At present, there is no way to specify skipping the first N partials in the synthesis. Since the oscs are not necessarily sorted by frequency, this requires a little fooling around. See the QuickSort (QIsort) in FindPartials for ideas. I think I would sort the oscillator numbers according to increasing frequency, and then testing OscOn I would skip over the first active oscillators in the loop to MaxOscs below. ; REQUIRE CrLf&" Need code to skip 1st N partials here "&CrLf MESSAGE; BEGIN "Synthesize" INTEGER IntIdx,Zosc,Nsamp,FpSinSiz; IFC UseFixedPoint THENC REQUIRE " Using fixed-point synthesis" MESSAGE; INTEGER ARRAY SynBuf[1:Nhop]; # Synthesis output buffer (for speed); INTEGER Y1,Y2,Y, Remain,Amp,Damp,Inc,Dinc,Phs; # Set up fixed-point number system (for maximum execution speed); DEFINE Nbits="14"; # No. bits to right of binary point; # Number of oscs summable is 2^(36-2*Nbits); DEFINE One = "(1 LSH Nbits)"; # A "1" in fixed-point; DEFINE R2Fp(x) = {((x) * One)}; # REAL to Fixed-Point (Fp), no round; DEFINE Fp2I(x) = {((x) ASH -Nbits)}; # Fp to INTEGER, no round; DEFINE Frac(x) = {((x) LAND (One-1))}; # Mask off fractional part; DEFINE FpFp(x,y)={((x)*(y) ASH -Nbits)}; # Fixed-point times fixed-point; ELSEC REQUIRE " Using floating-point synthesis"&CrLf MESSAGE; REAL ARRAY SynBuf[1:Nhop]; # Synthesis output buffer (for speed); REAL Y1,Y2,Y, Remain,Amp,Damp,Inc,Dinc,Phs; INTEGER PROCEDURE Floor(REAL x); RETURN(x); DEFINE One = "1"; DEFINE R2Fp(x) = {(x)}; DEFINE Fp2I(x) = { Floor(x) }; DEFINE Frac(x) = { (X-Floor(x)) }; DEFINE FpFp(x,y)={((x)*(y))}; ENDC IF Frame LEQ 1 THEN BEGIN "InitSine" REAL Pi,Dang; Pi <- 4*ATAN(1); Dang <- 2*Pi/SinSiz; FOR i <- 0 STEP 1 UNTIL SinSiz-1 DO SinBuf[i] <- R2Fp(SIN(i*Dang)); Mag <- SinSiz/Fs; END "InitSine"; FOR Zosc <- 1 STEP 1 UNTIL MaxOscs DO BEGIN "OscLoop" Amp <- R2Fp(PrvOscAmp[Zosc]); # Current amplitude (linear); Damp <- R2Fp(OscAmp[Zosc]-PrvOscAmp[Zosc])/Nhop; # Per-sample increment; IF Amp=Damp=0 # Only Noscs oscs are active; THEN CONTINUE "OscLoop"; # so avoid inactive ones; Inc <- R2Fp(Mag*PrvOscfrq[Zosc]); # Current table increment; Dinc <- R2Fp(Mag*(OscFrq[Zosc]-PrvOscfrq[Zosc])/Nhop); # Per-sample step; Phs <- OscPhs[Zosc]; # Current oscillator phase; FOR Nsamp <- 1 STEP 1 UNTIL Nhop DO # Synthesize one sinusoid; BEGIN "SynLoop" IntIdx <- Fp2I(Phs); # Sine table address; Remain <- Frac(Phs); # Linear interpolation amount; DEFINE SineMask = "(SinSiz-1)"; # For power-of-2 table length only; Y1 <- SinBuf[IntIdx LAND SineMask]; Y2 <- SinBuf[(IntIdx+1) LAND SineMask]; Y <- Y1 + FpFp(Remain,(Y2 - Y1)); SynBuf[Nsamp] <- SynBuf[Nsamp] + FpFp(Amp,Y); Amp <- Amp + Damp; Inc <- Inc + Dinc; Phs <- Phs + Inc; END "SynLoop"; FpSinSiz <- SinSiz*One; Phs <- (IF Phs GEQ FpSinSiz THEN Phs-FpSinSiz ELSE IF Phs<0 THEN Phs+FpSinSiz ELSE Phs); OscPhs[Zosc] <- Phs; END; FOR Nsamp <- Bp+1 STEP 1 UNTIL Bp+Nhop DO OutBuf[Nsamp] <- OutBuf[Nsamp] + (SynBuf[Nsamp-Bp]/One); # No rounding; END "Synthesize"; COMMENT Processing; GetWin(WinBuf,WinType,Nx); # Load window buffer; IF DoFlt THEN BEGIN FOR i <- 1 STEP 1 UNTIL Nh DO H[i] <- IC[i]; # Load filter into 1st part of buffer; TDpyEd(H,Nh,"Filter Impulse response"); !FFA(H,Nfft); # FFT filter impulse response; TDpyFFA(H,Nfft,"Filter spectrum",InF(Clock)); END; DBscl <- (10.0/LOG(10.0)); # Incredibly, this is not performed at compile time; Fs <- InF(Clock); Xp <- Bp <- Yp <- 0; # Input, OLA, and output sample pointers; PRINT("At time: "); DO BEGIN "RI" INTEGER i; PRINT(Cvfs(Xp/Fs)," "); ARRCLR(X); IF Xp+Nx>InF(#samps) THEN Nx <- InF(#samps) - Xp; Sandi(InF(Channel),Xp,Nx,X,InF(#samps),TRUE,InF(Pack)); Xp <- Xp + Nhop; Nhops <- Nhops + 1; Frame <- Xp/Nhop; Tdpyed(X,Nx,"Input frame "&CVS(Frame)); IF WinType>1 THEN FOR i <- 1 STEP 1 UNTIL Nx DO X[i] <- X[i] * WinBuf[i]; Tdpyed(X,Nx,"Windowed input frame "&CVS(Frame)); !FFA(X, Nfft); TDpyFFA(X,Nfft,"Windowed input frame spectrum",Fs); FOR i <- 1 STEP 2 UNTIL Nfft+1 DO BEGIN "DoFilter" INTEGER Ip1; REAL Xi,Hi,Xip1,Hip1; Ip1 <- i+1; Xi <- X[i]; Hi <- H[i]; Xip1 <- X[Ip1]; Hip1 <- H[Ip1]; XmagDB[(i+1) % 2] <- DBscl*LOG(Xi*Xi+Xip1*Xip1 MAX 1.0@-20); IF DoFlt THEN BEGIN X[i] <- Xi*Hi - Xip1*Hip1; X[Ip1] <- Xi*Hip1 + Xip1*Hi; END END "DoFilter"; IF SwapOut THEN BEGIN REAL ARRAY Xout[1:Nspec]; ARRTRAN(Xout,XmagDB); # Xout[1:257] gets clobbered if packing mode not 3; Tdpyed(Xout,Nspec,"*** OUTPUT DB (SWAP) SPECTRUM ***"); IF Sando(OutF(Channel),Yp,Nspec,Xout,OutH,Yp,TRUE,OutF(Pack)) THEN PRINT(" *** Sando unhappy ***",CrLf); PRINT(" * "); END; FindPartials(Nactive[Frame] <- MaxLins,XmagDB,LinAmpDB,LinFrq,Fs,MinSep, Thresh,Hyst,Nfft,Frame,MinWid,Fc1,Fc2); FOR i <- 1 Thru Nactive[Frame] DO LinAmp[i] <- 10^(LinAmpDB[i]/20)*SigScl; UpdateMap; # Unravel partials into consistent tracks (for synthsis); FOR CurOsc <- 1 Thru MaxOscs DO BEGIN "AmpsFrqs" Amps[CurOsc,Frame] <- OscAmp[CurOsc]; Frqs[CurOsc,Frame] <- OscFrq[CurOsc]; END "AmpsFrqs"; # TDpyFFA(X,Nfft,"Filtered windowed input frame spectrum",Fs); IF DoFlt THEN BEGIN "ola" !FFS(X, Nfft); # Inverse FFT (unnecessarily slow); Tdpyed(X,Nx+Nh,"Filtered windowed input frame"); FOR i <- Bp+1 STEP 1 UNTIL Bp+Nfft DO OutBuf[i] <- OutBuf[i] + X[i-Bp]; # For hack; END "ola"; IF DoSynth THEN BEGIN "callsynth" Tdpyed(OutBuf,Bp+Nhop,"OLA buffer BEFORE additive synthesis"); Synthesize(Nhop,Bp,Fs,Frame); # Generate synthesis up to sample Bp+Nhop in OutBuf; Tdpyed(OutBuf,Bp+Nhop,"OLA buffer AFTER additive synthesis"); END "callsynth"; IF NOT SwapOut THEN BEGIN Bp <- Bp + Nhop; IF Bp GEQ Nfft THEN IF DoOut THEN BEGIN "Wout" Tdpyed(OutBuf,Nfft,"*** OUTPUT OLA buffer BEFORE decimation"); Nout <- Decimate(OutBuf,Nfft,Ndec); # Downsample; Tdpyed(OutBuf,Nout,"*** OUTPUT OLA buffer AFTER decimation"); Sando(OutF(Channel),Yp,Nout,OutBuf,OutH,Yp,TRUE,OutF(Pack)); FOR i <- 1 STEP 1 UNTIL Nfft DO OutBuf[i] <- OutBuf[i+Nfft]; FOR i <- Nfft+1 STEP 1 UNTIL 2*Nfft DO OutBuf[i] <- 0; Bp <- Bp - Nfft; PRINT(" * "); END "Wout" END END "RI" UNTIL Xp GEQ InF(#samps) OR Trace=-999 OR Frame GEQ Nframes; TmpStr <- "PARSHL: From "&Idev&":"&Ifile&"; "& (IF DoFlt THEN "Filter="&Ffile ELSE NULL)&CrLf&Tab& (IF DoSynth THEN " AS" ELSE NULL)& " Nhops="&CVS(Nhops)& " Window="&WinStr& " Nfft="&CVS(Nfft)& " Nframe="&CVS(Nx)& " Nhop="&CVS(Nhop)& " Compression="&CVS(Ndec)&CrLf&Tab& " MinSpace="&Cvfs(MinSep)&"Hz"& " Lines="&CVS(MaxLins)& " Oscs="&CVS(MaxOscs)& " FirstFrq="&Cvfs(Fc1)&"Hz"& " LastFrq="&Cvfs(Fc2)&"Hz"&CrLf&Tab& " Thresh="&Cvfs(Thresh)&"dB"& " Hyst="&Cvfs(Hyst)&"dB"& " DFmax1="&Cvfs(DFmax1)&"Hz"& " UltDFmax="&Cvfs(DFmax2)&"Hz"&CrLf& " (+)"&Tab&InF(Text)&Crlf; IF DoOut THEN BEGIN "flush" Nout <- Decimate(OutBuf,Bp+Nh,Ndec); # Downsample; Sando(OutF(Channel),Yp,Nout,OutBuf,OutH,Yp,TRUE,OutF(Pack)); # Last piece; Sando(OutF(Channel),0,0,X,OutH,Yp,TRUE,OutF(Pack)); # Flush output buffer; WriteH(Head, OutF(Clock), OutF(Pack), OutF(#chans), OutF(#ticks), Maxamp, TmpStr); USETO (OutF(Channel), 1); ARRYOUT (OutF(Channel), Head [1], 128); RELEASE(InF(Channel)); RELEASE(OutF(Channel)); END "flush"; OutPartials(MaxOscs,Nframes,Amps,Frqs,Fs,Thresh); WriteH(Head, AmpF(Clock), AmpF(Pack), AmpF(#chans), AmpF(#ticks), Maxamp, TmpStr); USETO(AmpF(Channel),1); ARRYOUT(AmpF(Channel),Head[1],128); RELEASE(AmpF(Channel)); WriteH(Head, FrqF(Clock), FrqF(Pack), FrqF(#chans), FrqF(#ticks), Maxamp, TmpStr); USETO(FrqF(Channel),1); ARRYOUT(FrqF(Channel),Head[1],128); RELEASE(FrqF(Channel)); IF Trace THEN BEGIN REAL ARRAY TmpRA[1:Nframes]; FOR i <- 1 STEP 1 UNTIL Nframes DO TmpRA[i] <- Nactive[i]; DpyEd(TmpRA,Nframes,"Number of active partials versus frame number") END; END "ALAR"; PRINT("R R;REDUCE to convert Amplitudes and Frequencies to SEG functions",CrLf); PRINT("R R;SND2MF to convert Amplitudes and Frequencies to MERGE file format",CrLf); END "PARSHL".
Next Section:
Bibliography
Previous Section:
Future Prospects








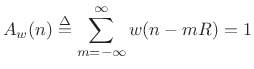
![\includegraphics[width=\twidth]{eps/fig4}](http://www.dsprelated.com/josimages_new/sasp2/img3048.png)
![\includegraphics[width=\twidth]{eps/fig5}](http://www.dsprelated.com/josimages_new/sasp2/img3049.png)
![\includegraphics[width=\twidth]{eps/fig6}](http://www.dsprelated.com/josimages_new/sasp2/img3076.png)











