Welch's Method with Windows

As usual, the purpose of the window function (Chapter 3) is to reduce side-lobe level in the spectral density estimate, at the expense of frequency resolution, exactly as in the case of sinusoidal spectrum analysis.

When using a non-rectangular analysis window, the window hop-size cannot exceed half the frame length without introducing a non-uniform sensitivity to the data over time. In the rectangular window case, we can set and have non-overlapping windows. For Hamming, Hanning, and any other generalized Hamming window, one normally sees for odd-length windows. For the Blackman window, is typical. In general, the hop size is chosen so that the analysis window overlaps and adds to a constant at that hop size. This consideration is explored more fully in Chapter 8. An equivalent parameter used by most matlab implementations is the overlap parameter .

Note that the number of blocks averaged in (6.27) increases as decreases. If denotes the total number of signal samples available, then the number of complete blocks available for averaging may be computed as

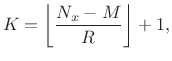(7.28)

Matlab for Welch's Method

Octave and the Matlab Signal Processing Toolbox have a pwelch function. Note that these functions also provide confidence intervals (not covered here). Matlab for generating the data shown in Fig.6.1 (employing Welch's method) appears in Fig.6.2.

M = 32;
Ks=[1 8 32 128]
nkases = length(Ks);
for kase = 1:4
  K = Ks(kase);
  N = M*K;
  Nfft = 2*M; % zero pad for acyclic autocorrelation
  Sv = zeros(Nfft,1); % PSD "accumulator"
  for m=1:K
    v = randn(M,1);  % noise sample
    V = fft(v,Nfft);
    Vms = abs(V).^2; % same as conj(V) .* V
    Sv = Sv + Vms;   % sum scaled periodograms
  end
  Sv = Sv/K;     % average of all scaled periodograms
  rv = ifft(Sv); % Average Bartlett-windowed sample autocor.
  rvup = [rv(Nfft-M+1:Nfft)',rv(1:M)']; % unpack FFT
  rvup = rvup/M; % Normalize for no bias at lag 0
end

Sign in