Chapter Outline
- ``Introduction to the DFT'' points out the mathematical
elements which will be discussed in this book, all motivated by the
DFT.
- ``Introduction to Complex Numbers'' is about factoring
polynomials, the quadratic formula, the complex plane, and Euler's
formula.
- ``Proof of Euler's Identity'' derives Euler's identity
in detail. This is an important tool for working with complex
numbers, and one of the critical elements of the DFT definition we
need to understand.
- ``Sinusoids and Exponentials'' is devoted to two of the
most elementary signals in signal processing--sinusoids and
exponentials. Also covered are complex sinusoids, audio decay
time (
 ), in-phase and quadrature sinusoidal components,
analytic signals, positive and negative frequencies, constructive and
destructive interference, invariance of sinusoidal frequency in linear
time-invariant systems, circular motion as the vector sum of in-phase
and quadrature sinusoidal motions, sampled sinusoids, and generating
sampled sinusoids from powers of a unit-modulus complex number.
), in-phase and quadrature sinusoidal components,
analytic signals, positive and negative frequencies, constructive and
destructive interference, invariance of sinusoidal frequency in linear
time-invariant systems, circular motion as the vector sum of in-phase
and quadrature sinusoidal motions, sampled sinusoids, and generating
sampled sinusoids from powers of a unit-modulus complex number.
- ``Geometric Signal Theory'' provides an introduction to
vector spaces, inner products, orthogonality, projection of one signal
onto another, norms, and elementary vector space operations. In this
setting, the DFT can be regarded as a change of coordinates from one
basis set (shifted impulses) to another (sinusoids at different
frequencies).
- ``The DFT Derived'' derives the DFT as a projection of a
length
 signal
signal 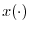 onto the set of
onto the set of  sampled complex
sinusoids generated by the
sampled complex
sinusoids generated by the  th roots of unity.
th roots of unity.
- ``Fourier Theorems for the DFT'' derives basic Fourier
symmetry relations, the shift theorem, convolution theorem,
correlation theorem, power theorem, and theorems pertaining to
interpolation and downsampling.
- ``Example Applications of the DFT'' illustrates
practical FFT analysis in Matlab
 and Octave (an open-source
matlab) through a series of examples. The various Fourier theorems of
the preceding chapter provide a ``thinking vocabulary'' for
understanding these applications.
and Octave (an open-source
matlab) through a series of examples. The various Fourier theorems of
the preceding chapter provide a ``thinking vocabulary'' for
understanding these applications.
Elementary and supporting information is provided in a series of appendices. Topics include introductions to sampling theory, Taylor series expansions, logarithms, decibels, digital audio number systems, matrices, round-off noise, Fourier series, and continuous-time Fourier theorems, such as the similarity and differentiation theorems. As a segue to computer-based approaches, a well used Fast Fourier Transform (FFT) algorithm is derived. Finally, various software examples in the Matlab (or Octave) programming language are presented.
This book is first in a series of course readers for my signal processing courses at CCRMA:
- Mathematics of the Discrete Fourier Transform (DFT):
http://www.dsprelated.com/dspbooks/mdft/ - Introduction to Digital Filters:
http://www.dsprelated.com/dspbooks/filters/ - Physical Audio Signal Processing
(the ``physical modeling book''):
http://www.dsprelated.com/dspbooks/pasp/ - Spectral Audio Signal Processing
(the ``spectral modeling book''):
http://www.dsprelated.com/dspbooks/sasp/ - Audio Digital Filter Design
(an update of Chapter 1 of my PhD/EE thesis [66]):
http://ccrma.stanford.edu/~jos/adfd/
Next Section:
Acknowledgments
Previous Section:
Index for this Document



















