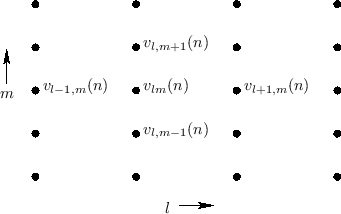
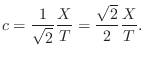DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Digital Waveguide Mesh

In §C.12, the theory of multiport scattering was derived, i.e., the reflections and transmissions that occur when $ N$ digital waveguides having wave impedances $ R_i$ are connected together. It was noted that when $ N$ is a power of two, there are no multiplies in the scattering relations Eq.$ \,$(C.105), and that this fact has been used to build multiply-free reverberators and other structures using digital waveguide meshes [430,518,146,396,520,521,398,399,401,55,202,321,320,322,422,33].

The Rectilinear 2D Mesh

Figure C.32: The 2D rectilinear digital waveguide mesh.
\includegraphics[width=4in]{eps/SchematicWaveguideMesh}

Figure C.32 shows the basic layout of the rectilinear 2D waveguide mesh. It can be thought of as simulating a plane using 1D digital waveguides in the same way that a tennis racket acts as a membrane composed of 1D strings.

At each node (string intersection), we have the following simple formula for the node velocity $ v$ in terms of the four incoming traveling-wave components:

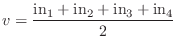
$\displaystyle v = \frac{\mbox{in}_{1} + \mbox{in}_{2} + \mbox{in}_{3} + \mbox{in}_{4}}{2} $

By continuity of velocity in a series connection (all string endpoints must move together at the node), the outgoing velocity-wave components must be given by

$\displaystyle \hbox{out}_k = v -$   in$\displaystyle _{k}, \qquad k=1,2,3,4. $

Dispersion

Since the digital waveguide mesh is lossless by construction (when modeling lossless membranes and volumes), and since it is also linear and time-invariant by construction, being made of ordinary digital filtering computations, there is only one type of error exhibited by the mesh: dispersion. Dispersion can be quantified as an error in propagation speed as a function of frequency and direction along the mesh. The mesh geometry (rectilinear, triangular, hexagonal, tetrahedral, etc.) strongly influences the dispersion properties. Many cases are analyzed in [55] using von Neumann analysis (see also Appendix D).

The triangular waveguide mesh [146] turns out to be the simplest mesh geometry in 2D having the least dispersion variation as a function of direction of propagation on the mesh. In other terms, the triangular mesh is closer to isotropic than all other known elementary geometries. The interpolated waveguide mesh [398] can also be configured to optimize isotropy, but at a somewhat higher compuational cost.

Recent Developments

An interesting approach to dispersion compensation is based on frequency-warping the signals going into the mesh [399]. Frequency warping can be used to compensate frequency-dependent dispersion, but it does not address angle-dependent dispersion. Therefore, frequency-warping is used in conjunction with an isotropic mesh.

The 3D waveguide mesh [518,521,399] is seeing more use for efficient simulation of acoustic spaces [396,182]. It has also been applied to statistical modeling of violin body resonators in [203,202,422,428], in which the digital waveguide mesh was used to efficiently model only the ``reverberant'' aspects of a violin body's impulse response in statistically matched fashion (but close to perceptually equivalent). The ``instantaneous'' filtering by the violin body is therefore modeled using a separate equalizer capturing the important low-frequency body and air modes explicitly. A unified view of the digital waveguide mesh and wave digital filters (§F.1) as particular classes of energy invariant finite difference schemes (Appendix D) appears in [54]. The problem of modeling diffusion at a mesh boundary was addressed in [268], and maximally diffusing boundaries, using quadratic residue sequences, was investigated in [279]; an introduction to this topic is given in §C.14.6 below.

2D Mesh and the Wave Equation

Figure C.33: Region of nodes in a rectilinear waveguide mesh.
\includegraphics{eps/mesh}

Figure C.34: Zoom-in about node $ (l,m)$ at time $ n$ in a rectilinear waveguide mesh, showing traveling-wave components entering and leaving the node. (All variables are at time $ n$,)
\includegraphics{eps/meshzoom}

Consider the 2D rectilinear mesh, with nodes at positions $ x=lX$ and $ y=mY$, where $ l$ and $ m$ are integers, and $ X$ and $ Y$ denote the spatial sampling intervals along $ x$ and $ y$, respectively (see Fig.C.33). Then from Eq.$ \,$(C.105) the junction velocity $ v_{lm}$ at time $ n$ is given by

$\displaystyle v_{lm}(n) = \frac{1}{2}\left[ v_{lm}^{+\textsc{n}}(n) + v_{lm}^{+\textsc{e}}(n) + v_{lm}^{+\textsc{s}}(n) + v_{lm}^{+\textsc{w}}(n)\right] $

where $ v_{lm}^{+\textsc{n}}(n)$ is the ``incoming wave from the north'' to node $ (l,m)$, and similarly for the waves coming from east, west, and south (see Fig.C.34).

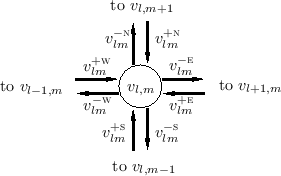
These incoming traveling-wave components arrive from the four neighboring nodes after a one-sample propagation delay. For example, $ v_{lm}^{+\textsc{n}}(n)$, arriving from the north, departed from node $ (l,m+1)$ at time $ n-1$, as $ v_{l,m+1}^{-\textsc{s}}(n-1)$. Furthermore, the outgoing components at time $ n$ will arrive at the neighboring nodes one sample in the future at time $ n+1$. For example, $ v_{lm}^{-\textsc{n}}(n)$ will become $ v_{l,m+1}^{+\textsc{s}}(n+1)$. Using these relations, we can write $ v_{lm}(n+1)$ in terms of the four outgoing waves from its neighbors at time $ n$:

$\displaystyle v_{lm}(n+1) = \frac{1}{2}\left[ v_{l,m+1}^{-\textsc{s}}(n) + v_{l... ...}}(n) + v_{l,m-1}^{-\textsc{n}}(n) + v_{l-1,m}^{-\textsc{e}}(n)\right] \protect$ (C.116)

where, for instance, $ v_{lm}^{-\textsc{n}}(n)$ is the ``outgoing wave to the north'' from node $ (l,m)$. Similarly, the outgoing waves leaving $ v_{lm}(n-1)$ become the incoming traveling-wave components of its neighbors at time $ n$:

$\displaystyle v_{lm}(n-1) = \frac{1}{2}\left[ v_{l,m+1}^{+\textsc{s}}(n) + v_{l... ...}}(n) + v_{l,m-1}^{+\textsc{n}}(n) + v_{l-1,m}^{+\textsc{e}}(n)\right] \protect$ (C.117)

This may be shown in detail by writing

\begin{eqnarray*} v_{lm}(n-1) &=& \frac{1}{2}[v_{lm}^{+\textsc{n}}(n-1) + \cdot... ...}^{-\textsc{n}}(n-1) + \cdots + v_{lm}^{-\textsc{w}}(n-1)\right] \end{eqnarray*}

so that

\begin{eqnarray*} v_{lm}(n-1) &=& \frac{1}{2}[v_{lm}^{-\textsc{n}}(n-1) + \cdot... ... v_{l,m-1}^{+\textsc{n}}(n) + v_{l-1,m}^{+\textsc{e}}(n)\right]. \end{eqnarray*}

Adding Equations (C.116-C.116), replacing terms such as $ v_{l,m+1}^{+\textsc{s}}(n) + v_{l,m+1}^{-\textsc{s}}(n)$ with $ v_{l,m+1}(n)$, yields a computation in terms of physical node velocities:

\begin{eqnarray*} \lefteqn{v_{lm}(n+1) + v_{lm}(n-1) = } \\ & & \frac{1}{2}\left[ v_{l,m+1}(n) + v_{l+1,m}(n) + v_{l,m-1}(n) + v_{l-1,m}(n)\right] \end{eqnarray*}

Thus, the rectangular waveguide mesh satisfies this equation giving a formula for the velocity at node $ (l,m)$, in terms of the velocity at its neighboring nodes one sample earlier, and itself two samples earlier. Subtracting $ 2v_{lm}(n)$ from both sides yields

\begin{eqnarray*} \lefteqn{v_{lm}(n+1) - 2 v_{lm}(n) + v_{lm}(n-1)} \\ &=& \fra... .... \left[v_{l+1,m}(n) - 2 v_{lm}(n) + v_{l-1,m}(n)\right]\right\} \end{eqnarray*}

Dividing by the respective sampling intervals, and assuming $ X=Y$ (square mesh-holes), we obtain

\begin{eqnarray*} \lefteqn{\frac{v_{lm}(n+1) - 2 v_{lm}(n) + v_{lm}(n-1)}{T^2}} ... ...ft.\frac{v_{l+1,m}(n) - 2 v_{lm}(n) + v_{l-1,m}(n)}{X^2}\right]. \end{eqnarray*}

In the limit, as the sampling intervals $ X,Y,T$ approach zero such that $ X/T = Y/T$ remains constant, we recognize these expressions as the definitions of the partial derivatives with respect to $ t$, $ x$, and $ y$, respectively, yielding

$\displaystyle \frac{\partial^2 v(t,x,y)}{\partial t^2} = \frac{X^2}{2T^2} \left... ...^2 v(t,x,y)}{\partial x^2} + \frac{\partial^2 v(t,x,y)}{\partial y^2} \right]. $

This final result is the ideal 2D wave equation $ \ddot v = c^2 \nabla^2 v$, i.e.,

$\displaystyle \frac{\partial^2 v}{\partial t^2} = c^2 \left[ \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} \right] $

with

$\displaystyle c = \frac{1}{\sqrt{2}}\frac{X}{T} = \frac{\sqrt{2}}{2}\frac{X}{T}. \protect$ (C.118)

Discussion regarding solving the 2D wave equation subject to boundary conditions appears in §B.8.3. Interpreting this value for the wave propagation speed $ c$, we see that every two time steps of $ 2T$ seconds corresponds to a spatial step of $ \sqrt{2}X$ meters. This is the distance from one diagonal to the next in the square-hole mesh. We will show later that diagonal directions on the mesh support exact propagation (of plane waves traveling at 45-degree angles with respect to the $ x$ or $ y$ axes). In the $ x$ and $ y$ directions, propagation is highly dispersive, meaning that different frequencies travel at different speeds. The exactness of 45-degree angles can be appreciated by considering Huygens' principle on the mesh.

The Lossy 2D Mesh

Because the finite-difference form of the digital waveguide mesh is the more efficient computationally than explicitly computing scattering wave variables (too see this, count the multiplies required per node), it is of interest to consider the finite-difference form also in the case of frequency-dependent losses. The method of §C.5.5 extends also to the waveguide mesh, which can be shown by generalizing the results of §C.14.4 above using the technique of §C.5.5.

The basic idea is once again that wave propagation during one sampling interval (in time) is associated with linear filtering by $ G(z)$. That is, $ G(z)$ is regarded as the per-sample wave propagation filter.

Diffuse Reflections in the Waveguide Mesh

In [416], Manfred Schroeder proposed the design of a diffuse reflector based on a quadratic residue sequence. A quadratic residue sequence $ a_p(n)$ corresponding to a prime number $ p$ is the sequence $ n^2$ mod $ p$, for all integers $ n$. The sequence is periodic with period $ p$, so it is determined by $ a_p(n)$ for $ n=0,1,2,\ldots,p-1$ (i.e., one period of the infinite sequence).

For example, when $ p=7$, the first period of the quadratic residue sequence is given by

\begin{eqnarray*} a_7 &=& [0^2,1^2,2^2,3^2,4^2,5^2,6^2] \quad (\mbox{mod }7)\\ &=& [0, 1, 4, 2, 2, 4, 1] \end{eqnarray*}

An amazing property of these sequences is that their Fourier transforms have precisely constant magnitudes. That is, the sequence

$\displaystyle c_p(n) \isdef e^{j\frac{2\pi}{p} a_p(n)} $

has a DFT with exactly constant magnitude:C.11

$\displaystyle \vert C_p(\omega_k)\vert \isdef \vert\dft _k(c_p)\vert \isdef \l... ...^{p-1} c_p(n) e^{-j2\pi nk/p}\right\vert = \sqrt{p}, \quad \forall k\in[0,p-1] $

This property can be used to give highly diffuse reflections for incident plane waves.

Figure C.35 presents a simple matlab script which demonstrates the constant-magnitude Fourier property for all odd integers from 1 to 99.

Figure C.35: Matlab script for demonstrating the Fourier property of an odd-length quadratic residue sequence.
  
function [c] = qrsfp(Ns)
%QRSFP Quadratic Residue Sequence Fourier Property demo
  if (nargin<1)
     Ns = 1:2:99; % Test all odd integers from 1 to 99
  end
  for N=Ns
    a = mod([0:N-1].^2,N);
    c = zeros(N-1,N);
    CM = zeros(N-1,N);
    c = exp(j*2*pi*a/N);
    CM = abs(fft(c))*sqrt(1/N);
    if (abs(max(CM)-1)>1E-10) || (abs(min(CM)-1)>1E-10)
       warn(sprintf("Failure for N=%d",N));
    end
  end
  r = exp(2i*pi*[0:100]/100); % a circle
  plot(real(r), imag(r),"k"); hold on;
  plot(c,"-*k"); % plot sequence in complex plane
end

Quadratic residue diffusers have been applied as boundaries of a 2D digital waveguide mesh in [279]. An article reviewing the history of room acoustic diffusers may be found in [94].

Next Section:
FDNs as Digital Waveguide Networks
Previous Section:
Two Coupled Strings