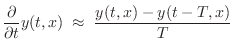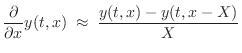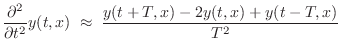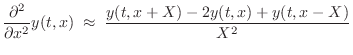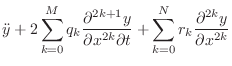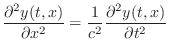Free Books    Physical Audio Signal Processing  

Finite-Difference Schemes

This appendix gives some simplified definitions and results from the subject of finite-difference schemes for numerically solving partial differential equations. Excellent references on this subject include Bilbao [53,55] and Strikwerda [481].

The simplifications adopted here are that we will exclude nonlinear and time-varying partial differential equations (PDEs). We will furthermore assume constant step-sizes (sampling intervals) when converting PDEs to finite-difference schemes (FDSs), i.e., sampling rates along time and space will be constant. Accordingly, we will assume that all initial conditions are bandlimited to less than half the spatial sampling rate, and that all excitations over time (such as summing input signals or ``moving boundary conditions'') will be bandlimited to less than half the temporal sampling rate. In short, the simplifications adopted here make the subject of partial differential equations isomorphic to that of linear systems theory [449]. For a more general and traditional treatment of PDEs and their associated finite-difference schemes, see, e.g., [481].

Finite-Difference Schemes

Finite-Difference Schemes (FDSs) aim to solve differential equations by means of finite differences. For example, as discussed in §C.2, if $ y(t,x)$ denotes the displacement in meters of a vibrating string at time $ t$ seconds and position $ x$ meters, we may approximate the first- and second-order partial derivatives by

$\displaystyle {\dot y}(t,x)$ $\displaystyle \isdef$ $\displaystyle \frac{\partial}{\partial t}y(t,x) \;\approx\; \frac{y(t,x)-y(t-T,x)}{T}$  
$\displaystyle y'(t,x)$ $\displaystyle \isdef$ $\displaystyle \frac{\partial}{\partial x}y(t,x) \;\approx\; \frac{y(t,x)-y(t,x-X)}{X}$  
$\displaystyle {\ddot y}(t,x)$ $\displaystyle \isdef$ $\displaystyle \frac{\partial^2}{\partial t^2} y(t,x) \;\approx\; \frac{y(t+T,x) - 2 y(t,x) + y(t-T,x) }{T^2}$  
$\displaystyle y''(t,x)$ $\displaystyle \isdef$ $\displaystyle \frac{\partial^2}{\partial x^2} y(t,x) \;\approx\; \frac{y(t,x+X) - 2 y(t,x) + y(t,x-X) }{X^2} \protect$ (D.1)

where $ T$ denotes the time sampling interval and $ X$ denotes the spatial sampling interval. Other types of finite-difference schemes were derived in Chapter 7 (§7.3.1), including a look at frequency-domain properties. These finite-difference approximations to the partial derivatives may be used to compute solutions of differential equations on a discrete grid:

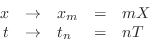
\begin{displaymath} \begin{array}{rclcl} x &\to& x_m&=& mX\nonumber \\ t &\to& t_n&=& nT\nonumber \end{array}\end{displaymath}

Let us define an abbreviated notation for the grid variables

$\displaystyle y_{n,m}\isdef y(nT,mX) $

and consider the ideal string wave equation (cf, §C.1):

$\displaystyle y''= \frac{1}{c^2}{\ddot y} \protect$ (D.2)

where $ c$ is a positive real constant (which turns out to be wave propagation speed). Then, as derived in §C.2, setting $ X=cT$ and substituting the finite-difference approximations into the ideal wave equation leads to the relation

$\displaystyle y_{n+1,m}+ y_{n-1,m}= y_{n,m+1}+ y_{n,m-1} $

everywhere on the time-space grid (i.e., for all $ n$ and $ m$). Solving for $ y_{n+1,m}$ in terms of displacement samples at earlier times yields an explicit finite-difference scheme for string displacement:

$\displaystyle y_{n+1,m}= y_{n,m+1}+ y_{n,m-1}- y_{n-1,m} \protect$ (D.3)

The FDS is called explicit because it was possible to solve for the state at time $ n$ as a function of the state at earlier times (and any other positions $ m$). This allows it to be implemented as a time recursion (or ``digital filter'') which computes a solution at time $ n$ from solution samples at earlier times (and any spatial positions). When an explicit FDS is not possible (e.g., a non-causal filter is derived), the discretized differential equation is said to define an implicit FDS. An implicit FDS can often be converted to an explicit FDS by a rotation of coordinates [55,481].

Convergence

A finite-difference scheme is said to be convergent if all of its solutions in response to initial conditions and excitations converge pointwise to the corresponding solutions of the original differential equation as the step size(s) approach zero.

In other words, as the step-size(s) shrink, the FDS solution must improve, ultimately converging to the corresponding solution of the original differential equation at every point of the domain.

In the vibrating string example, the limit is taken as the step sizes (sampling intervals) $ T$ and $ X$ approach zero. Since the finite-difference approximations in Eq.$ \,$(D.1) converge in the limit to the very definitions of the corresponding partial derivatives, we expect the FDS in Eq.$ \,$(D.3) based on these approximations to be convergent (and it is).

In establishing convergence, it is necessary to provide that any initial conditions and boundary conditions in the finite-difference scheme converge to those of the continuous differential equation, in the limit. See [481] for a more detailed discussion of this topic.

The Lax-Richtmyer equivalence theorem provides a means of showing convergence of a finite-difference scheme by showing it is both consistent and stable (and that the initial-value problem is well posed) [481]. The following subsections give basic definitions for these terms which applicable to our simplified scenario (linear, shift-invariant, fixed sampling rates).

Consistency

A finite-difference scheme is said to be consistent with the original partial differential equation if, given any sufficiently differentiable function $ y(t,x)$, the differential equation operating on $ y(t,x)$ approaches the value of the finite difference equation operating on $ y(nT,mX)$, as $ T$ and $ X$ approach zero.

Thus, in the ideal string example, to show the consistency of Eq.$ \,$(D.3) we must show that

$\displaystyle \left(\frac{\partial^2}{\partial x^2} - \frac{1}{c^2} \frac{\par... ...eft[ (\delta_x + \delta_x^{-1}) - (\delta_t + \delta_t^{-1}) \right] y_{n,m} $

for all $ y(t,x)$ which are second-order differentiable with respect to $ t$ and $ x$. On the right-hand side, we have introduced the following shift operator notation:
$\displaystyle \delta_t^k y_{n,m}$ $\displaystyle \isdef$ $\displaystyle y_{n-k,m}$  
$\displaystyle \delta_x^k y_{n,m}$ $\displaystyle \isdef$ $\displaystyle y_{n,m-k} \protect$ (D.4)

In particular, we have

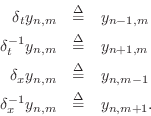
\begin{eqnarray*} \delta_t y_{n,m}&\isdef & y_{n-1,m}\\ \delta_t^{-1} y_{n,m}&\... ...&\isdef & y_{n,m-1}\\ \delta_x^{-1} y_{n,m}&\isdef & y_{n,m+1}. \end{eqnarray*}

In taking the limit as $ T$ and $ X$ approach zero, we must maintain the relationship $ X=cT$, and we must scale the FDS by $ 1/X^2$ in order to achieve an exact result:

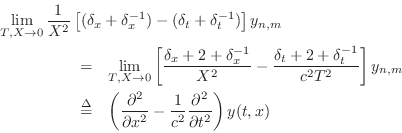
\begin{eqnarray*} \lefteqn{\lim_{T,X\to0} \frac{1}{X^2} \left[ (\delta_x + \del... ... - \frac{1}{c^2} \frac{\partial^2}{\partial t^2} \right)y(t,x) \end{eqnarray*}

as required. Thus, the FDS is consistent. See, e.g., [481] for more examples.

In summary, consistency of a finite-difference scheme means that, in the limit as the sampling intervals approach zero, the original PDE is obtained from the FDS.

Well Posed Initial-Value Problem

For a proper authoritative definition of ``well posed'' in the field of finite-difference schemes, see, e.g., [481]. The definition we will use here is less general in that it excludes amplitude growth from initial conditions which is faster than polynomial in time.

We will say that an initial-value problem is well posed if the linear system defined by the PDE, together with any bounded initial conditions is marginally stable.

As discussed in [449], a system is defined to be stable when its response to bounded initial conditions approaches zero as time goes to infinity. If the response fails to approach zero but does not exponentially grow over time (the lossless case), it is called marginally stable.

In the literature on finite-difference schemes, lossless systems are classified as stable [481]. However, in this book series, lossless systems are not considered stable, but only marginally stable.

When marginally stable systems are allowed, it is necessary to accommodate polynomial growth with respect to time. As is well known in linear systems theory, repeated poles can yield polynomial growth [449]. A very simple example is the ordinary differential equation (ODE)

$\displaystyle {\ddot y}= 0 $

which, given the initial condition $ y(0)$, has solutions

$\displaystyle y(t) = y(0) + ct $

for any constant $ c$. Thus, the system is lossless and the initial condition is finite, yet solution is not bounded. Similarly, solutions to the ODE $ {\dddot y}=0$ can grow as $ t^2$, and so on.

When all poles of the system are strictly in the left-half of the Laplace-transform $ s$ plane, the system is stable, even when the poles are repeated. This is because exponentials are faster than polynomials, so that any amount of exponential decay will eventually overtake polynomial growth and drag it to zero in the limit.

Marginally stable systems arise often in computational physical modeling. In particular, the ideal string is only marginally stable, since it is lossless. Even a simple unaccelerated mass, sliding on a frictionless surface, is described by a marginally stable PDE when the position of the mass is used as a state variable (see §7.1.2). Given any nonzero initial velocity, the position of the mass approaches either $ +$ or $ -$ infinity, exactly as in the $ {\ddot y}=0$ example above. To avoid unbounded growth in practical systems, it is often preferable to avoid the use of displacement as a state variable. For ideal strings and freely sliding masses, force and velocity are usually good choices.

It should perhaps be emphasized that the term ``well posed'' normally allows for more general energy growth at a rate which can be bounded over all initial conditions [481]. In this book, however, the ``marginally stable'' case (at most polynomial growth) is what we need. The reason is simply that we wish to excluded unstable PDEs as a modeling target. Note, however, that unstable systems can be used profitable over carefully limited time durations (see §9.7.2 for an example).

In the ideal vibrating string, energy is conserved. Therefore, it is a marginally stable system. To show mathematically that the PDE Eq.$ \,$(D.2) is marginally stable, we may show that

$\displaystyle \left\Vert\,y(t,x)\,\right\Vert _2^2(t) = \alpha \left\Vert\,y(0,x)\,\right\Vert _2^2 + \beta \left\Vert\,{\dot y}(0,x)\,\right\Vert _2^2. $

for some constants $ \alpha$ and $ \beta$. I.e., we can show

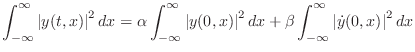
$\displaystyle \int_{-\infty}^{\infty} \left\vert y(t,x)\right\vert^2 dx = \alp... ...t^2 dx + \beta\int_{-\infty}^{\infty} \left\vert{\dot y}(0,x)\right\vert^2 dx $

for all $ t$.

Note that solutions on the ideal string are not bounded, since, for example, an infinitely long string (non-terminated) can be initialized with a constant positive velocity everywhere along its length. This corresponds physically to a nonzero transverse momentum, which is conserved. Therefore, the string will depart in the positive $ y$ direction, with an average displacement that grows linearly with $ t$.

The well-posedness of a class of damped PDEs used in string modeling is analyzed in §D.2.2.

A Class of Well Posed Damped PDEs

A large class of well posed PDEs is given by [45]

$\displaystyle {\ddot y} + 2\sum_{k=0}^M q_k \frac{\partial^{2k+1}y}{\partial x^{2k}\partial t} + \sum_{k=0}^N r_k\frac{\partial^{2k}y}{\partial x^{2k}} \protect$ (D.5)

Thus, to the ideal string wave equation Eq.$ \,$(C.1) we may add any number of even-order partial derivatives in $ x$, plus any number of mixed odd-order partial derivatives in $ x$ and $ t$, where differentiation with respect to $ t$ occurs only once. Because every member of this class of PDEs is only second-order in time, it is guaranteed to be well posed, as we now show.

To show Eq.$ \,$(D.5) is well posed [45], we must show that the roots of the characteristic polynomial equation (§D.3) have negative real parts, i.e., that they correspond to decaying exponentials instead of growing exponentials. To do this, we may insert the general eigensolution

$\displaystyle y(t,x) = e^{st+vx}$

into the PDE just like we did in §C.5 to obtain the so-called characteristic polynomial equation:

$\displaystyle s^2 + 2q(v)s + r(v) = 0 $

where

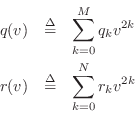
\begin{eqnarray*} q(v) &\isdef & \sum_{k=0}^M q_k v^{2k}\\ r(v) &\isdef & \sum_{k=0}^N r_k v^{2k} \end{eqnarray*}

Let's now set $ v=jk$, where $ k=2\pi/\lambda$ is radian spatial frequency (called the ``wavenumber'' in acoustics) and of course $ j=\sqrt{-1}$, thereby converting the implicit spatial Laplace transform to a spatial Fourier transform. Since there are only even powers of the spatial Laplace transform variable $ v$, the polynomials $ q(jk)$ and $ r(jk)$ are real. Therefore, the roots of the characteristic polynomial equation (the natural frequencies of the time response of the system), are given by

$\displaystyle s = -q \pm \sqrt{q^2 - r}. $

Proof that the Third-Order Time Derivative is Ill Posed

For its tutorial value, let's also show that the PDE of Ruiz [392] is ill posed, i.e., that at least one component of the solution is a growing exponential. In this case, setting $ y(t,x) = e^{st+jkx}$ in Eq.$ \,$(C.28), which we restate as

$\displaystyle Ky''= \epsilon {\ddot y}+ \mu{\dot y}+ \mu_3{\dddot y}, $

yields the characteristic polynomial equation

$\displaystyle p(s,jk) = \mu_3 s^3 + \epsilon s^2 + \mu s + Kk^2 = 0. $

By the Routh-Hurwitz theorem, there is at least one root in the right-half $ s$-plane.

It is interesting to note that Ruiz discovered the exponentially growing solution, but simply dropped it as being non-physical. In the work of Chaigne and Askenfelt [77], it is believed that the finite difference approximation itself provided the damping necessary to eliminate the unstable solution [45]. (See §7.3.2 for a discussion of how finite difference approximations can introduce damping.) Since the damping effect is sampling-rate dependent, there is an upper bound to the sampling rate that can be used before an unstable mode appears.

Stability of a Finite-Difference Scheme

A finite-difference scheme is said to be stable if it forms a digital filter which is at least marginally stable [449].

To distinguish between the stable and marginally stable cases, we may classify a finite-difference scheme as strictly stable, marginally stable, or unstable.

Lax-Richtmyer equivalence theorem

The Lax-Richtmyer equivalence theorem states that ``a consistent finite-difference scheme for a partial differential equation for which the initial-value problem is well posed is convergent if and only if it is stable.'' For a proof, see [481, Ch. 10].

Passivity of a Finite-Difference Scheme

A condition stronger than stability as defined above is passivity. Passivity is not a traditional metric for finite-difference scheme analysis, but it arises naturally in special cases such as wave digital filters (§F.1) and digital waveguide networks [55,35]. In such modeling frameworks, all signals have a physical interpretation as wave variables, and therefore a physical energy can be associated with them. Moreover, each delay element can be associated with some real wave impedance. In such situations, passivity can be defined as the case in which all impedances are nonnegative. When complex, they must be positive real (see §C.11.2).

To define passivity for all linear, shift-invariant finite difference schemes, irrespective of whether or not they are based on an impedance description, we will say that a finite-difference scheme is passive if all of its internal modes are stable. Thus, passivity is sufficient, but not necessary, for stability. In other words, there are finite difference schemes which are stable but not passive [55]. A stable FDS can have internal unstable modes which are not excited by initial conditions, or which always cancel out in pairs. A passive FDS cannot have such ``hidden'' unstable modes.

The absence of hidden modes can be ascertained by converting the FDS to a state-space model and checking that it is controllable (from initial conditions and/or excitations) and observable [449]. When the initial conditions can set the entire initial state of the FDS, it is then controllable from initial conditions, and only observability needs to be checked. A simple example of an unobservable mode is the second harmonic of an ideal string (and all even-numbered harmonics) when the only output observation is the midpoint of the string.

Summary

In summary, we have defined the following terms from the analysis of finite-difference schemes for the linear shift-invariant case with constant sampling rates:

  • PDE well posed $ \Leftrightarrow$ PDE at least marginally stable
  • FDS consistent 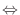$ \Leftrightarrow$ FDS shift operator 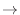$ \to$ PDE operator as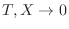 $ T,X\to0$
  • FDS stable 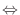$ \Leftrightarrow$ stable or marginally stable as a digital filter
  • FDS strictly stable 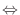$ \Leftrightarrow$ stable as a digital filter
  • FDS marginally stable 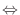$ \Leftrightarrow$ marginally stable as a digital filter
Finally, the Lax-Richtmyer equivalence theorem establishes that well posed + consistency + stability implies convergence, where, as defined in §D.2 above, convergence means that solutions of the FDS approach corresponding solutions of the PDE as $ T,X\to0$.

Convergence in Audio Applications

Because the range of human hearing is bounded (nominally between 20 and 20 kHz), spectral components of a signal outside this range are not audible. Therefore, when the solution to a differential equation is to be considered an audio signal, there are frequency regions over which convergence is not a requirement.

Instead of pointwise convergence, we may ask for the following two properties:

  • Superposition holds.
  • Convergence occurs within the frequency band of human hearing.
Superposition holds for all linear partial differential equations with constant coefficients (linear, shift-invariant systems [449]). We need this condition so that errors in the inaudible bands do not affect the audible bands. Inaudible errors are fine as long as they do not grow so large that they cause numerical overflow. An example in which this ``bandlimited design'' approach yields large practical dividends is in bandlimited interpolator design (see §4.4).

In many cases, such as in digital waveguide modeling of vibrating strings, we can do better than convergence. We can construct finite difference schemes which agree with the corresponding continuous solutions exactly at the sample points. (See §C.4.1.)

Characteristic Polynomial Equation

The characteristic polynomial equation for a linear PDE with constant coefficients is obtained by taking the 2D Laplace transform of the PDE with respect to $ x$ and $ t$. A simple way of doing this is to substitute the general eigensolution

$\displaystyle y(t,x) = e^{st+vx}$ (D.6)

into the PDE, where $ s=\sigma+j\omega$ denotes the complex variable associated with the Laplace-transform with respect to time, and $ v=\beta+jk$ is the complex variable associated with the spatial Laplace transform.

As a simple example, the ideal-string wave equation (analyzed in §C.1) is a simple second-order PDE given by

$\displaystyle \frac{\partial^2 y(t,x)}{\partial x^2} = \frac{1}{c^2} \frac{\partial^2 y(t,x)}{\partial t^2} \protect$ (D.7)

where $ c$ is a positive constant (sound speed, as discussed in §C.1).

Substituting Eq.$ \,$(D.6) into Eq.$ \,$(D.7) results in the following characteristic polynomial equation:

$\displaystyle v^2 - \frac{1}{c^2}s^2 = 0 $

Solving for $ s$ in terms of $ v$ gives the so-called dispersion relation:

$\displaystyle s = \pm c v $

or, looking only at the frequency axes (i.e., using Fourier transforms in place of Laplace transforms),

$\displaystyle \omega = \pm c k. $

Since the phase velocity of a traveling wave is, by definition, the temporal frequency divided by spatial frequency, we have simply

$\displaystyle v_p \isdef \frac{\omega}{k} = \pm c. $

This result can be interpreted as saying that all Fourier components of any solution of Eq.$ \,$(D.7) must propagate along the string with speed $ c$ to either the left or the right along the string. In more general PDEs, propagation may be dispersive, in which case the phase velocity depends on frequency (see §C.6 for an analysis of stiff vibrating strings, which are dispersive). Moreover, wave propagation may be damped in a frequency-dependent way, in which case one or more roots of the characteristic polynomial equation will have negative real parts; if any roots have positive real parts, we say the initial-value problem is ill posed since is has exponentially growing solutions in response to initial conditions.

Von Neumann Analysis

Von Neumann analysis is used to verify the stability of a finite-difference scheme. We will only consider one time dimension, but any number of spatial dimensions.

The procedure, in principle, is to perform a spatial Fourier transform along all spatial dimensions, thereby reducing the finite-difference scheme to a time recursion in terms of the spatial Fourier transform of the system. The system is then stable if this time recursion is at least marginally stable as a digital filter.

Let's apply von Neumann analysis to the finite-difference scheme for the ideal vibrating string Eq.$ \,$(D.3):

$\displaystyle y_{n+1,m}= y_{n,m+1}+ y_{n,m-1}- y_{n-1,m} \protect$

There is only one spatial dimension, so we only need a single 1D Discrete Time Fourier Transform (DTFT) along $ m$ [451]. Using the shift theorem for the DTFT, we obtain
$\displaystyle Y_{n+1}(k)$ $\displaystyle =$ $\displaystyle (e^{jkX} + e^{-jkX})Y_n(k) - Y_{n-1}(k)$  
  $\displaystyle =$ $\displaystyle 2\cos(kX)Y_n(k) - Y_{n-1}(k)$  
  $\displaystyle \isdef$ $\displaystyle 2c_kY_n(k) - Y_{n-1}(k) \protect$ (D.8)

where $ k=2\pi/\lambda$ denotes radian spatial frequency (wavenumber). (On a more elementary level, the DTFT along $ m$ can be carried out by substituting $ Y_n(k)e^{jkX}$ for $ y(n,m)$ in the finite-difference scheme.) This is now a second-order difference equation (digital filter) that needs its stability checked. This can be accomplished most easily using the Durbin recursion [449], or we can check that the poles of the recursion do not lie outside the unit circle in the $ z$ plane.

A method equivalent to checking the pole radii, and typically used when the time recursion is first order, is to compute the amplification factor as the complex gain $ G(k)$ in the relation

$\displaystyle Y_{n+1}(k) = G(k)Y_n(k). $

The finite-difference scheme is then declared stable if $ \vert G(k)\vert\leq 1$ for all spatial frequencies $ k$.

Since the finite-difference scheme of the ideal vibrating string is so simple, let's find the two poles. Taking the z transform of Eq.$ \,$(D.8) yields

$\displaystyle zY(z,k) = 2c_k Y(z,k) - z^{-1}Y(z,k) $

yielding the following characteristic polynomial:

$\displaystyle z^2 - 2c_k z - 1 = 0 $

Applying the quadratic formula to find the roots yields

$\displaystyle z = c_k \pm \sqrt{c_k^2 - 1}. $

The squared pole moduli are then given by

$\displaystyle \left\vert z\right\vert^2 = c_k^2 \pm (c_k^2 - 1) = \left\{\begi... ...eq 1 \\ [5pt] [1,1], & \left\vert c_k\right\vert\leq 1 \\ \end{array}\right.. $

Thus, for marginal stability, we require $ \left\vert c_k\right\vert\leq 1$, and the poles become

$\displaystyle z = c_k \pm j\sqrt{1-c_k^2} = \cos(kX) \pm j\sin(kX) = e^{\pm jkX}. $

Since the range of spatial frequencies is $ k\in[-\pi/X,\pi/X]$, we spontaneously have $ \vert c_k\vert\leq1$ for all $ k$. Therefore, we have shown by von Neumann analysis that the finite-difference scheme Eq.$ \,$(D.3) for the ideal vibrating string is stable.

In summary, von Neumann analysis verifies that no spatial Fourier components in the system are growing exponentially with respect to time.

Next Section:
Equivalence of Digital Waveguide and Finite Difference Schemes
Previous Section:
Digital Waveguide Theory